К какому типу уравнений относятся волновые уравнения

Волновое и телеграфное уравнения

Уравнение

(2.59)

где скорость распространения волны в данной среде, называется волновым уравнением. В приведенном уравнении обозначают декартовы координаты точки, время.

Для двумерного пространства (плоский случай) волновое уравнение имеет вид

.

(2.60)

В одномерной области уравнение (2.60) принимает вид

.

(2.61)

Волновое уравнение описывает процессы распространения упругих, звуковых, световых, электромагнитных волн, а также другие колебательные явления. Например, волновое уравнение может описать:

а) малые поперечные колебания струны (при этом под понимают поперечное отклонение точки струны от положения равновесия в момент времени );

б) продольные колебания упругого стержня ( продольное отклонение частицы от ее положения при отсутствии деформации);

в) малые упругие колебания плоской пластины, мембраны;

г) течение жидкости или газа в коротких трубах, когда трением о стенки трубы можно пренебречь ( давление или расход).

(2.62)

называется телеграфным уравнением. Оно описывает электрические колебания в проводах ( сила тока или напряжение), неустановившееся течение жидкости или газа в трубах ( давление или скорость).

Волновое и телеграфное уравнения входят в группу уравнений гиперболического типа.

Уравнение теплопроводности

Уравнение

(2.63)

где параметр, учитывающий физические свойства изучаемой среды, называется уравнением теплопроводности.

Оно имеет вид для плоского случая

(2.64)

.

(2.65)

Уравнением теплопроводности описываются процессы нестационарного массо- и теплообмена. В частности, к этим уравнениям приводят задачи о неустановившемся режиме распределения тепла (при этом означает коэффициент температуропроводности, а температуру в любой точек исследуемой области в любой момент времени ), о фильтрации упругой жидкости в упругой пористой среде, например, нефти и газа в подземных песчаниках ( коэффициент пьезопроводности, давление в любой точке среды), о неустановившейся диффузии ( коэффициент диффузии, концентрация), о течении жидкости в магистральных трубопроводах ( давление или скорость жидкости).

Если при рассмотрении этих задач окажется, что в исследуемой области функционируют внутренние источники и стоки массы или тепла, то процесс описывается неоднородным уравнением

,

(2.66)

где функция характеризует интенсивность функционирующих источников.

Уравнения (2.63) – (2.66) являются простейшими уравнениями параболического типа.

Уравнения Лапласа и Пуассона

Уравнение

(2.67)

называется уравнением Пуассонав трехмерном пространстве. Если в этом уравнении , то оно называется уравнением Лапласа:

.

(2.68)

К исследованию уравнений Лапласа и Пуассона приводит рассмотрение задач о стационарном процессе: это задачи гидродинамики, диффузии, распределения температуры, электростатики и др.

Эти уравнения относятся к уравнениям эллиптического типа.

Те задачи, которые приводят к уравнениям, содержащим время, называются нестационарными или динамическими задачами математической физики; задачи, приводящие к уравнениям, не содержащим время, называются стационарными или статическими.

Как было показано, уравнения математической физики имеют бесчисленное множество решений, зависящие от двух произвольных функций (речь идет об уравнениях второго порядка для функции двух переменных). Для того, чтобы из множества решений выделить определенное, характеризующее процесс, необходимо на искомую функцию наложить дополнительные условия, которые диктуются физическими соображениями. Таковыми условиями для уравнений в частных производных являются, чаще всего, начальные и граничные условия. Граничные условия – это условия заданные на границе рассматриваемой среды; начальные условия – это условия, относящиеся к какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Дополнительные условия, так же как и само дифференциальное уравнение, выводятся на основе физических соображений, связанных с самим процессом. Вместе с тем дополнительные условия должны быть такими, чтобы обеспечить выделение единственного решения из всего множества решений. Число граничных и начальных условий определяются типом уравнения, а их вид – заданным исходным состоянием на границе объекта и внешней среды. Для рассматриваемых нами уравнений число начальных условий равно порядку старшей производной по времени, входящей в уравнение, а число граничных условий – порядку старшей производной по координате.

Совокупность дифференциального уравнения и дополнительных условий представляют собой математическую формулировку физической задачи, и называется задачей математической физики.

Итак, задача математической физики состоит в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям, скажем, граничным и начальным.

Задача математической физики считается поставленной корректно, если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво.

2.19 КОЛЕБАНИЯ СТРУНЫ. ГРАНИЧНЫЕ И НАЧАЛЬНЫЕ УСЛОВИЯ. ПОСТАНОВКА КРАЕВЫХ ЗАДАЧ

Пусть струна находится под действием сильного начального натяжения . Если вывести струну из положения равновесия и подвергнуть действию какой-либо силы, то струна начнет колебаться. Процесс колебания можно описать одной функцией , характеризующей вертикальное перемещение струны (отклонение от положения равновесия (рис. 2.2)). При каждом фиксированном значении график функции на плоскости дает форму струны в момент времени .

Функция удовлетворяет уравнению

,

(2.69)

где масса единицы длины (линейная плотность струны), сила, действующая на струну перпендикулярно оси и рассчитанная на единицу длины.

Если внешняя сила отсутствует, т.е. , то уравнение

(2.70)

описывает свободные колебания струны без воздействия внешних усилий.

Уравнение (2.69) является простейшим уравнением гиперболического типа и в то же время одним из важнейших уравнений матфизики.

Одного уравнения движения (2.69) или (2.70) при математическом описании физического процесса недостаточно. При рассмотрении задачи о колебании струны дополнительные условия могут быть двух видов: начальные и граничные (краевые).

Так как процесс колебаний струны зависит от ее начальной формы и распределения скоростей, то следует задать начальные условия:

.

(2.71)

Граничные условия определяются поддерживаемым на концах струны режимом на протяжении процесса колебания. Так, если концы струны длины

закреплены, то отклонения в точках и равны нулю:

.

(2.72)

Будем говорить о трех типах граничных условий:

I

II

III ,

где известные функции,

и известные постоянные.

Приведенные условия называют соответственно граничными условиями первого, второго, третьего рода. Условия I имеют место в том случае, когда концы объекта (струна, стержень и т.д.) перемещаются по заданному закону; условия II – в случае, когда к концам приложены заданные силы; условия III – в случае упругого закрепления концов.

Если функции, заданные в правой части равенства, равны нулю, то граничные условия называются однородными. Так, граничные условия (2.72) – однородные. Комбинируя различные перечисленные типы граничных условий, получим шесть типов простейших краевых задач.

В том случае, когда режим на концах не будет оказывать существенного влияния на ту часть струны, которая достаточно удалена от них, струну считают бесконечной. В силу этого вместо полной краевой задачи ставят предельную задачу – з а д а ч у К о ш и: найти решение уравнения (2.69) для при , удовлетворяющее начальным условиям

.

Если изучается процесс вблизи одной границы и влияние граничного режима на второй границе не имеет существенного значения на протяжении интересующего нас промежутка времени, то приходим к постановке задачи на полуограниченной прямой . В этом случае задаются начальные условия и одно из граничных условий I — III при .

Примеры решения задач

ПРИМЕР 2.42. Однородная струна длины совершает малые поперечные колебания. Поставить задача об определении отклонений точек струны от прямолинейного положения покоя, если в момент струна имела форму ( ) и скорость каждой ее точки задается функцией . Рассмотреть случаи:

а) концы струны закреплены;

б) концы струны свободны;

в) к концам струны и , начиная с момента , приложены поперечные силы и соответственно;

г) концы струны закреплены упруго, т.е. каждый из концов испытывает сопротивление, пропорциональное отклонению конца.

Решение. Как известно, отклонения точек струны от положения равновесия удовлетворяют в отсутствии действующей внешней силы уравнению свободных колебаний (2.70)

.

Здесь , натяжение, линейная плотность , т.к. струна однородная.

Начальные условия имеют вид:

, , .

Займемся выводом граничных условий.

Случай а). Так как концы струны закреплены, то их отклонения в точках и должны быть равными нулю при любом , т.е.

, , .

Итак, физическая задача о колебаниях закрепленной на концах струны свелась к следующей математической задаче: найти функцию , определенную при и , являющуюся решением уравнения

и удовлетворяющую граничным условиям

,

и начальным условиям

, .

Случай б). Если концы струны свободны, то внешние силы, приложенные к ним, равны нулю. И, следовательно, равна нулю сила натяжения , которая согласно закону Гука, пропорциональна удлинению: , где коэффициент включает модуль упругости материала. Поэтому

, , ,

Задача формулируется следующим образом: найти решение уравнения

, , ,

удовлетворяющее граничным условиям

,

и начальным условиям

, .

Случай в). Рассмотрим граничные элементы и . Запишем второй закон Ньютона для правого элемента , на который действует сила и сила натяжения :

Переходя к пределу при , получим

, откуда .

Аналогично получим условия для левого конца:

.

Таким образом, задача ставится так: найти в области , , решение уравнения

,

удовлетворяющее граничным условиям рода

,

и начальным условиям

, .

Случай г). При упругом закреплении концов каждый конец испытывает сопротивление, пропорциональное отклонению конца, т.е.

, ,

где — коэффициент жесткости упругого крепления концов струны. Тогда из граничных условий в случае в) получим

, ,

иначе , .

Математическая формулировка задачи: найти решение уравнения

,

удовлетворяющее граничным условиям III рода

, ,

и начальным условиям

, , .

Основные типы уравнений математической физики

Основные типы уравнений

К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.

1. Волновое уравнение:

.

Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т. д.

2. Уравнение теплопроводности, или уравнение Фурье:

.

Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т. д.

3. Уравнение Лапласа:

.

Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т. д.

В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных. Например, волновое уравнение с тремя независимыми переменными имеет вид

,

и уравнение Лапласа

.

Уравнение колебаний струны.

Формулировка краевой задачи

В математической физике струной называют гибкую упругую нить. Пусть струна в начальный момент времени расположена на отрезке 0≤x≤l оси Ox. Предположим, что ее концы закреплены в точках x=0 и x=l. Если струну отклонить от первоначального положения, а потом предоставить самой себе или придать ее точкам некоторую скорость, то точки струны будут совершать движение. Задача заключается в определении формы струны в любой момент времени и в определении закона движения каждой точки струны в зависимости от времени.

Если предположить, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости, то процесс колебания струны описывается одной функцией u(x,t), которая определяет величину перемещения точки струны с абсциссой x в момент t.

Доказано, что при отсутствии внешней силы функция u(x,t) должна удовлетворять дифференциальному уравнению в частных производных второго порядка

.

Для полного определения движения струны одного уравнения недостаточно. Искомая функция u(x,t) должна удовлетворять граничным условиям, указывающим, что делается на концах струны (при x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, концы струны при x=0 и x=l неподвижны. Тогда при любом t должны выполняться равенства

Это – граничные условия для рассматриваемой задачи. В начальный момент t=0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f(x), т. е.

Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(x), т. е.

.

Эти два условия называются начальными условиями.

Колебания бесконечной струны.

Формула Даламбера решения задачи Коши

для волнового уравнения

Прежде чем решать задачу о колебаниях закрепленной струны, рассмотрим более простую задачу – о колебаниях бесконечной струны. Если представить очень длинную струну, то ясно, что на колебания, возникающие в ее средней части, концы струны не будут оказывать заметного влияния.

Рассматривая свободные колебания, мы должны решить однородное уравнение

при начальных условиях

, ,

где функции f(x) и g(x) заданы на всей числовой оси. Такая задача называется задачей с начальными условиями или задачей Коши.

Преобразуем волновое уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

интегралами которых служат прямые

Введем новые переменные ξ=x – at, η=x + at и запишем волновое уравнение для переменных ξ и η.

, ,

,

,

и подставляя их в исходное уравнение, видим, что уравнение колебания струны в новых координатах будет

.

Интегрируя полученное равенство по η при фиксированном ξ, придем к равенству . Интегрируя это равенство по ξ при фиксированном η, получим

,

где φ и ψ являются функциями только переменных ξ и η соответственно. Следовательно, общим решением исходного уравнения является функция

. (8)

Найдем функции φ и ψ так, чтобы удовлетворялись начальные условия:

.

,

.

Интегрируя последнее равенство, получим:

,

где х0 и С – постоянные. Из системы уравнений

Таким образом, мы определили функции φ и ψ через заданные функции f и g, причем полученные равенства должны иметь место для любого значения аргумента. Подставляя в (8) найденные значения φ и ψ, будем иметь

.

Найденное решение называется формулой Даламбера решения задачи Коши для волнового уравнения

Пример. Решить уравнение при начальных условиях , .

Используя формулу Даламбера, сразу получаем

.

Решение волнового уравнения

методом разделения переменных

Метод разделения переменных применяется для решения многих задач математической физики. Пусть требуется найти решение волнового уравнения

, (9)

удовлетворяющее краевым условиям

u(x,0)=f(x), . (12),(13)

Частное решение уравнения (9), удовлетворяющее граничным условиям (10) и (11), ищут в виде произведения двух функций:

Подставляя функцию u(x,t) в уравнение (9) и преобразовывая его, получим

.

В левой части этого уравнения стоит функция, которая не зависит от x, а в правой – функция, не зависящая от t. Равенство возможно только в том случае, когда левая и правая части не зависят ни от x, ни от t, т. е. равны постоянному числу. Обозначим

, где λ>0. (14)

Из этих уравнений получаем два однородных дифференциальных уравнения второго порядка с постоянными коэффициентами

и . (15)

Общее решение этих уравнений

,

,

где A, B, C, D – произвольные постоянные.

Постоянные A и B подбирают так, чтобы выполнялись условия (10) и (11), из которых следует, что X(0)=X(l)=0, так как T(t)≠0 (в противном случае u(x,t)=0). Учитывая полученные равенства, находим

А=0 и .

Так как B≠0 (иначе, было бы X=0 и u=0, что противоречит условию), то должно выполняться равенство

,

.

Найденные значения λ называют собственными значениями для данной краевой задачи. Соответствующие им функции X(x) называются собственными функциями.

Заметим, что, если в равенстве (14) вместо – λ взять число λ (λ>0), то первое из уравнений (15) будет иметь решение в виде

.

Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (10) и (11).

Зная , можем записать

.

Для каждого n получаем решение уравнения (9)

.

Так как исходное уравнение (9) линейное и однородное, то сумма решений также является решением, и потому функция

(16)

будет решением дифференциального уравнения (9), удовлетворяющим граничным условиям (10) и (11).

Найденное частное решение должно еще удовлетворять начальным условиям (12) и (13). Из условия (12) получим

.

Далее, дифференцируя члены ряда (16) по переменной t, из условия (13) будем иметь

.

Правые части двух последних равенств есть ряды Фурье для функций f(x) и φ(x), разложенных по синусам на интервале (0, l). Поэтому

. (17)

Итак, ряд (16), для которого коэффициенты Cn и Dn определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (9), удовлетворяющее граничным и начальным условиям.

Пример. Найти решение краевой задачи для волнового уравнения

, 0

К какому типу уравнений относятся волновые уравнения

Волновое уравнение
_{Wave equation}

Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением

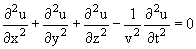(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид

u(x,t) = Asin(ωt − xv).

Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T

Частота ω и период колебаний T связаны соотношением

Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x

u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).

u(r,t) = (A/r)sin(ωt − kr).

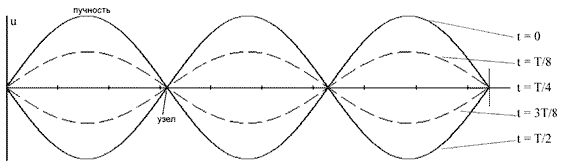
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.

Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.

Соотношение (2) можно получить, используя формулу

sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]

и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.