Введение в математическое моделирование — тест 4
Упражнение 1: Номер 1
Ответ:
Упражнение 2: Номер 1
Ответ:
Упражнение 3: Номер 1
Ответ:
Упражнение 4: Номер 1
Ответ:
Упражнение 5: Номер 1
Ответ:
Упражнение 6: Номер 1
Ответ:
Упражнение 7: Номер 1
Ответ:
Упражнение 8: Номер 1
Ответ:
Упражнение 9: Номер 1
Ответ:
Упражнение 10: Номер 1
Ответ:
Упражнение 11: Номер 1
Ответ:
Упражнение 12: Номер 1
Ответ:
Решение нелинейных уравнений
Содержание
· Решение нелинейных уравнений
Отделение корней
Уточнение корней до заданной точности
Решение нелинейных уравнений
Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.
Дано алгебраическое уравнение
Определить интервалы локализации корней этого уравнения.
Чтобы решить задачу предварительной локализацией корней, в самых простых случаях можно использовать графическое представление f(x).
Понятно, что в случае многомерных систем такой способ практически неприменим. Если требуется исследовать определенную область определения переменных уравнения на наличие корней, определив их примерное положение, то обычно применяют весьма расточительный способ, называемый сканированием. Оно состоит в последовательном поиске корня, начиная из множества подобных точек, покрывающих расчетную область.
Пример организации упрощенного варианта сканирования по одной переменной приведен на рисунке 5.6. График функции, корни которой подлежат определению, показан в его верхней части. Затем осуществляется решение уравнения при помощи функции root, для нескольких последовательно расположенных узлов. Результат выдается в последней строке листинга в виде таблицы, из которой видно, что на рассматриваемом интервале уравнение имеет три корня.
Решение нелинейных уравнений
(Уточнение корней до заданной точности)
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных и многие другие.
Функция root.В MathCAD для уточнения корней любого нелинейного уравнения введена функция root, которая может иметь два или четыре аргумента, т.е. root(f(x),x) или root(f(x),x,a,b), где f(x)-имя функции или арифметическое выражение, х-скалярная переменная, относительно которой решается уравнение, a,b-границы интервала локализации корня
Пример (В MathCAD)
Решить уравнение 
1. Сначала вводиться функция 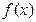
2. Задается точность
3. Графически находится приближенное решение уравнения (можно использовать трассировку)
4. При помощи функции 
5. Выполняется проверка найденного решения
Функция polyroots.Для вычисления всех корней алгебраического уравнения порядка n (не выше 5) рекомендуется использовать функциюpolyroots. Обращение к этой функции имеет вид polyroots(v),где v-вектор, состоящий из n+1 проекций, равных коэффициентам алгебраического уравнения, т.е. 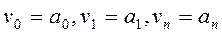
Пример (В MathCAD)
Решить уравнение
Блок Given.При уточнение корня нелинейного уравнения можно использовать специальный вычислительные блок Given, имеющий следующую структуру:
(Вызов функции Find или Minerr)
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно. Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(х), где х-переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(х), которая возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(х) и в появившемся контекстном меню выбрать подходящий алгоритм.
Если заданно уравнение f(x)=0, то его можно решить следующим образом с помощью блока Given-Find:
1. Задать начальное приближение
2. Ввести служебное слово
3. Записать уравнение, используя знак жирное равно
4. Написать функцию find с неизвестной переменной в качестве параметра
5. В результате после знака равно выведется найденный корень
Решить уравнение
Численные методы решения нелинейных уравнений
Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение:
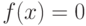 | ( 4.1) |
Необходимо решить это уравнение, т. е. найти его корень 
Если функция имеет вид многочлена степени m,
где ai — коэффициенты многочлена, 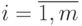
Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .
Такие уравнения обычно имеют бесконечное множество решений.
Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .
Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.
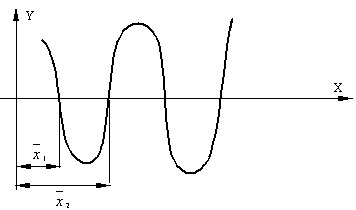
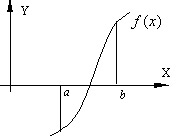
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).
Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
- отделение корней, — т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
- уточнение корней, — т.е. сужение интервала [a,b] до величины равной заданной степени точности
.
Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
http://megapredmet.ru/1-59222.html
http://intuit.ru/studies/courses/2260/156/lecture/27239




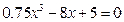



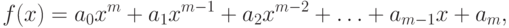
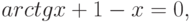

 .
.