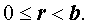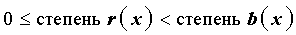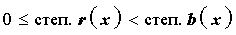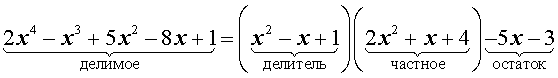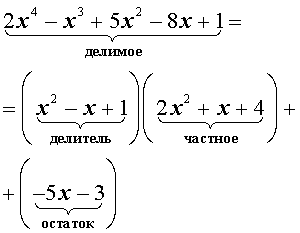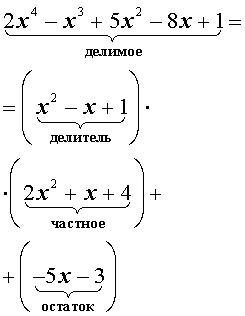Как делить уравнение на уравнение

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)

С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена

Немного теории.

Деление многочлена на многочлен (двучлен) столбиком (уголком)

В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).

Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов \( f(x) \) и \( g(x) \), \( g(x) \neq 0 \), существуют единственные полиномы \( q(x) \) и \( r(x) \), такие что
$$ \frac = q(x)+\frac $$
причем \( r(x) \) имеет более низкую степень, чем \( g(x) \).

Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного \( q(x) \) и остатка \( r(x) \) для заданных делимого \( f(x) \) и ненулевого делителя \( g(x) \)

Пример

Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac $$

Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой \( (x^3/x = x^2) \)

2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого \( (x^2 \cdot (x-3) = x^3-3x^2) \)

3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой \( (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) \)

4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.

5. Повторяем шаг 4.

6. Конец алгоритма.
Таким образом, многочлен \( q(x)=x^2-9x-27 \) — частное деления многочленов, а \( r(x)=-123 \) — остаток от деления многочленов.

Результат деления многочленов можно записать в виде двух равенств:
\( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 \)
или
$$ \frac = x^2-9x-27 + \frac<-123> $$

Алгоритм деления «уголком» многочленов от одной переменной

Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:

где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:

Если друг на друга делить многочлены, то возникает похожая ситуация.

Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

Однако в результате деления многочленов многочлен получается далеко не всегда.

Говорят, что один многочлен нацело (без остатка) делится на другой многочлен , если результатом деления является многочлен.

Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком , в результате которого и частное, и остаток будут многочленами.

Определение . Разделить многочлен a(x) на многочлен b(x) с остатком – это значит представить многочлен a(x) в виде

где многочлен c(x) – частное , а многочлен r(x) – остаток , причем, степень остатка удовлетворяет неравенству:

Очень важно отметить, что формула

является тождеством, т.е. равенством, справедливым при всех значениях переменной x .

При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

Один из способов деления многочленов с остатком – это деление многочленов «уголком» , что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

К описанию этого способа деления многочленов мы сейчас и переходим.

Пример . Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

Решение . Опишем алгоритм деления многочленов «уголком» по шагам:

Делим первый член делимого 2x 4 на первый член делителяx 2 . Получаем первый член частного 2x 2 .

Умножаем первый член частного 2x 2 наделительx 2 – x + 1, а результат умножения

пишем под делимым 2x 4 – x 3 + 5x 2 – 8x + 1 .

Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток

Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член остаткаx 3 на первый член делителяx 2 . Получаем второй член частного x .

Умножаем второй член частного x на делительx 2 – x + 1 , а результат умножения

пишем под первым остатком x 3 + 3x 2 – 8x .

Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член второго остатка 4x 2 на первый член делителяx 2 . Получаем третий член частного 4 .

Умножаем третий член частного 4 на делительx 2 – x + 1 , а результат умножения

пишем под вторым остатком.

Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток

Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен.

Запись изложенного процесса деления многочленов «уголком» имеет следующий вид: