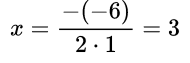Как доказать что уравнение имеет один корень

Определение 1. Пусть функция определена в некоторой окрестности точки . Придавая независимой переменной приращение х , невыводящее за пределы окрестности, получим новое значение + х , также принадлежащее окрестности . Тогда значение функции заменится новым значением , то есть получит приращение

Если существует предел отношения приращении функции у к вызвавшему его приращению независимой переменной х при стремлении х к 0, т.е. , то он называется производной функции в точке х и обозначается .

Операция вычисления производной называется операцией дифференцирования.

Образно говоря, равенство означает, что производная функции в точке х равна скорости изменения переменной у относительно переменой в указанной точке.

Определение 2. Функция , заданная в некоторой окрестности точки R называется дифференцируемой в этой точке, если ее приращение , представимо в этой окрестности в виде , где — постоянная, О( х) — бесконечно малая более высокого порядка, чем х.

Линейная функция (аргумента х ) называется дифференциалом функции в точке х и обозначается df(x или dy .

Таким образом, у = dy + О( х) , .

Можно доказать следующую теорему:

Теорема 1. Функция дифференцируема в некоторой точке в том и только том случае, когда в этой точке имеет конечную производную.

Учитывая определение 2 и утверждение теоремы, в качестве определения дифференцируемой функции может быть принято следующее:

Определение 3. Если функция у имеет производную в точке , то говорят, что при данном значении функция дифференцируема.

То есть существование производной функции в точке х равносильно ее дифференцируемости в этой точке.

Теорема 2 . Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.

Обратная теорема не верна: существуют функции, непрерывные в некоторой точке, но не дифференцируемые в этой точке.

Если функция определена в некоторой окрестности точки , принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х производную, то эта производная равна нулю.

1) непрерывна на отрезке [ ]

2) имеет в каждой точке интервала конечную производную,

3) принимает равные значения на концах отрезка [ ], то есть f(a) = f(b) , то существует, по крайней мере, одна такая точка , что .

Если функция непрерывна на отрезке [ ] и в каждой точке интервала имеет конечную или определенного знака бесконечную производную, то существует такая точка , что f(b) — f(a) = f ( (b — a).

Используя теорему Лагранжа, можно доказать следующие теоремы:

Условие постоянства функции

Теорема 3. (Условие постоянства функции) Пусть функция определена и непрерывна на промежутке Х и во всех его внутренних точках имеет конечную производную . Для того, чтобы была на указанном отрезке постоянной, необходимое и достаточное условие внутри Х.

Если две функции и определены и непрерывны в промежутке Х и внутри него имеют конечные производные и , причем (внутри Х), то эти функции на всем промежутке Х отличаются лишь на постоянную: (C = const).

Теорема 4. (Признак монотонности функций)

Для того чтобы дифференцируемая на интервале функция возрастала (убывала) на этом интервале, необходимо и достаточно, чтобы ее производная была во всех точках интервала неотрицательна (неположительна).

Если производная функция во всех точках интервала положительна (отрицательна), то функция строго возрастает (строго убывает) на этом интервале.

Если функции и непрерывны на отрезке [ ] и в каждой точке интервала имеют конечные производные , , причем для , а f(а) g(а) , тогда для любой точки выполняется неравенство .

На основании утверждения теоремы 5 для того, чтобы доказать неравенство f(x) 0 при х 0 , достаточно доказать, что f(0) 0 и (х) 0 при х 0 . А для того, чтобы доказать неравенство при , можно воспользоваться второй производной и при и т.д.

С помощью производной можно также определить число корней того или иного уравнения. Один из возможных приемов основан на следующей теореме:

Если функция определена и непрерывна на отрезке и во всех его внутренних точках имеет конечную производную, то между любыми двумя корнями этой функции, расположенными на отрезке, имеется хотя бы 1 корень ее производной.

Рассмотренные теоретические положения используются при решении задач.

Задача 1. Докажите тождество 3 arcsin x — arccos( 3 4 ) = , если .

Решение. Рассмотрим функцию 3 arcsinx — arccos( 3 4 на отрезке [ ]. Докажем, что f(х) = с, с = const. Для этого достаточно доказать, что (т.3)

Если , то следовательно, и . Для определения значения вычислим значение функции в произвольной точке интервала . Пусть , тогда и .

Вычислим значение функции на концах заданного отрезка.

Таким образом, тождество верно при любом .

Задача 2. Найдите сумму .

Решение. Представив искомую сумму в виде , заметим, что .

Используя формулу суммы членов геометрической прогрессии, получим,

Итак, искомая сумма имеет вид .

Используя полученную формулу, можно, например, вычислить

Задача 3. Найдите сумму:

Решение. Используя результат, полученный в примере 2, заметим, что

Задача 4. Решите уравнение:

Решение. Очевидно, что — корень уравнения. Докажем, что уравнение других корней не имеет. Рассмотрим функцию

Для функции точка является точкой минимума, в которой функция принимает наименьшее значение. Значит, для всех , отличных от нуля, > .

Задача 5. Решите уравнение:

Преобразуем уравнение к виду:

Рассмотрим функции и при .

Сравним множества значений этих функций. Очевидно, что .

Найдем с использованием производной.

Функция непрерывна на промежутке и имеет на нем единственную критическую точку , в которой достигает своего наибольшего значения.

Следовательно, решение уравнения находим из решения системы:

Рассмотрим функцию , при .

Функция непрерывна на промежутке и является возрастающей, . — является точкой минимума функции , в которой функция принимает наименьшее значение, ровное нулю. Следовательно, для всех > .

Таким образом, исходное уравнение имеет единственный корень .

Задача 6. Докажите, что уравнение может иметь не более трех различных корней.

Решение. Рассмотрим функцию . Функция является дифференцируемой на R . Предположим, что функция имеет более трех различных корней, например, четыре. Тогда должна иметь не более трех различных корней (т.6), то есть обращается в нуль не менее трех раз.

Функция дифференцируема на R . Ее производная обращается в нуль не менее двух раз. Тогда имеет не менее двух нулей, а ее производная не менее одного нуля. Но функция нулей не имеет. Получили противоречие. Значит, сделанное предположение неверно, функция более трех различных корней иметь не может. Таким образом, заданное уравнение может иметь не более трех различных корней.

Производную можно использовать при доказательстве и решении неравенств.

Задача 7. Доказать, что при 0$»>.

Доказательство. Докажем справедливость следующих неравенств:

0. \end —>

0. \end«>

(1)

Для доказательства неравенства (2) рассмотрим функцию

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

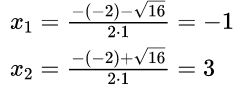
Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Как доказать что уравнение имеет один корень

Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.

Решите уравнение: `x^3 +4x^2 — 2x-3=0`.

Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:

`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`

Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.

Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.

Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что

`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.

Умножим обе части на `q^n`, получаем:

`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.

Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:

Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.

Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.

Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.

а) `x^4+4x^3-102x^2-644x-539=0`; (15)

б) `6x^4-35x^3+28x^2+51x+10=0`. (16)

а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:

Поэтому `p` может принимать значения:

Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:

Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:

1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.

2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.

б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:

Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем

Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:

Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.

К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.

Разложите на множители:

а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`

Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:

в) Вынесем `x^2` за скобки и сгруппируем:

Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:

В итоге получаем:

Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).

г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению

Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.

Прибегнем к методу неопределённых коэффициентов. Пусть

Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:

Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:

Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.

Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:

2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:

Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.

Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому

Далее каждый из квадратных трёхчленов можно разложить на множители.

Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.

источники:

http://spadilo.ru/kvadratnoe-uravnenie-i-diskriminant/

http://zftsh.online/articles/5013