Простейшие тригонометрические уравнения с тангенсом и котангенсом
Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).
Алгоритм решения простейших уравнений с тангенсом
Давайте с вами рассмотрим типичное уравнение, например, \(tgx=\sqrt<3>\).
Пример. Решить уравнение \(tgx=\sqrt<3>\).
Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…
…и обозначим то место на оси, куда мы должны попасть в итоге.
Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.
Точки найдены. Давайте подпишем значение одной из них…
…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: \(x=\frac<π><3>+πn\), \(n∈Z\).
Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется \(πn\), а не \(2πn\). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии \(π\). Благодаря этому значение обеих точек можно записать одной формулой в виде \(x=t_0+πn\), \(n∈Z\).
Пример. Решить уравнение \(tgx=-1\).
Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:
Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.
Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.
Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу \(x=t_0+πn\), \(n∈Z\) (подробнее о формуле в видео), где \(t_0\) – как раз то значение, которые вы нашли в шаге 4.
Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.
Алгоритм решения простейших уравнений с котангенсом
Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.
Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в \(\frac<1><\sqrt<3>>\) на оси котангенсов?
Строим круг, проводим нужные оси.
Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…
…и соединяем центр окружности и точку на оси котангенсов прямой линией.
По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…
…и записываем окончательный ответ по формуле \(x=t_0+πn\), \(n∈Z\), потому что у котангенса период такой же как у тангенса: \(πn\).
Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен \(\sqrt<3>\), котангенс будет \(\frac<1><\sqrt<3>>\).
Разберем еще пример, а потом подведем итог.
Пример. Решить уравнение \(ctgx=-1\). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.
Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:
Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.
Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.
Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.
Шаг 4. Найти значение одной из точек на круге.
Шаг 5. Записать ответ используя формулу \(x=t_0+πn\), \(n∈Z\), где \(t_0\) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.
Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции \(arctg\) и \(arcctg\). Если вы не знаете, что это – читайте эту статью.
Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
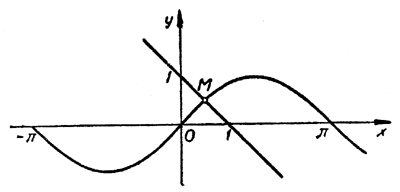
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
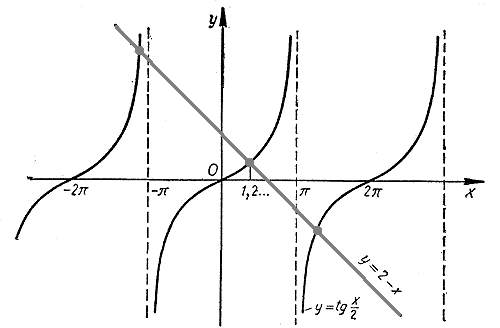
Графики функций у = tg x /2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Объяснение и обоснование
- Корни уравненияcosx=a.
При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)
2.Частые случаи решения уравнения sin x = a.
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
Примеры решения задач
Замечание. Ответ к задаче 1 часто записывают в виде:
19.3. Уравнения tg x = a и ctg x = a
Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке 
Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
таким образом, уравнение ctg x = 0 имеет корни
Примеры решения задач
Вопросы для контроля
- Какие уравнения называют простейшими тригонометрическими?
- Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
- Выведите формулы решения простейших тригонометрических уравнений.
- Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение (1-11)
Найдите корни уравнения на заданном промежутке (12-13)
http://razdupli.ru/teor/77_reshenie-trigonometricheskih-uravnenij-graficheski.php
http://ya-znau.ru/znaniya/zn/280