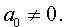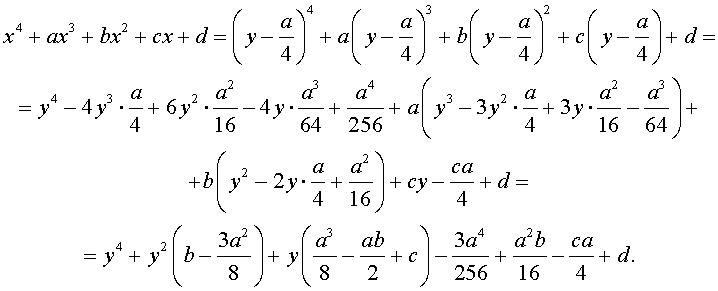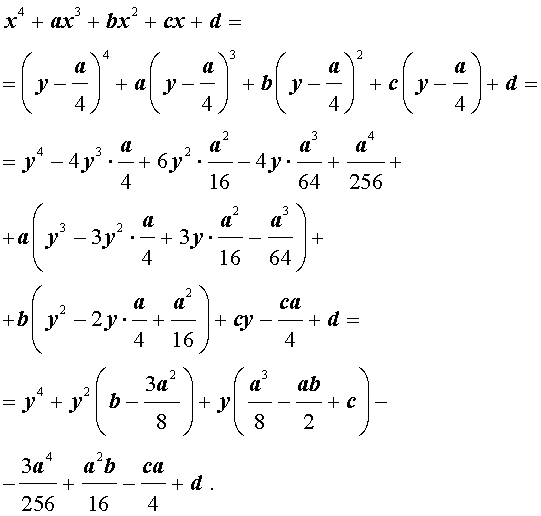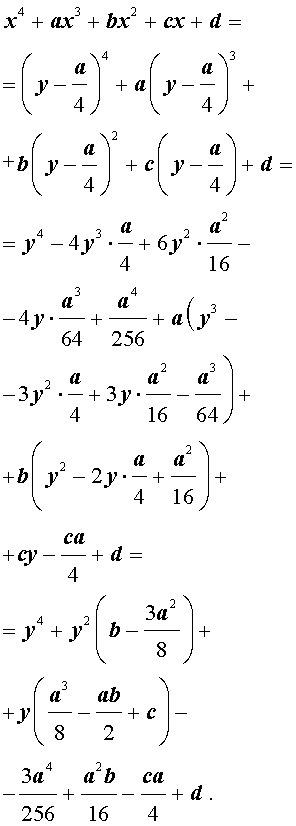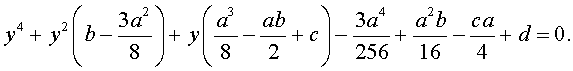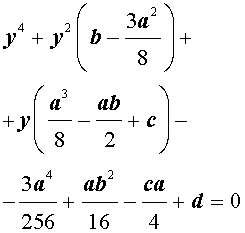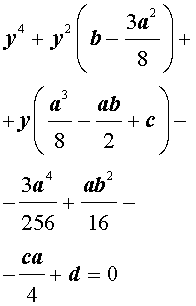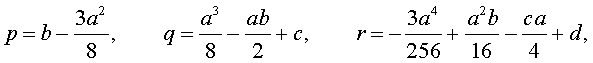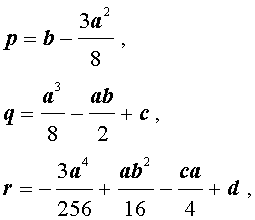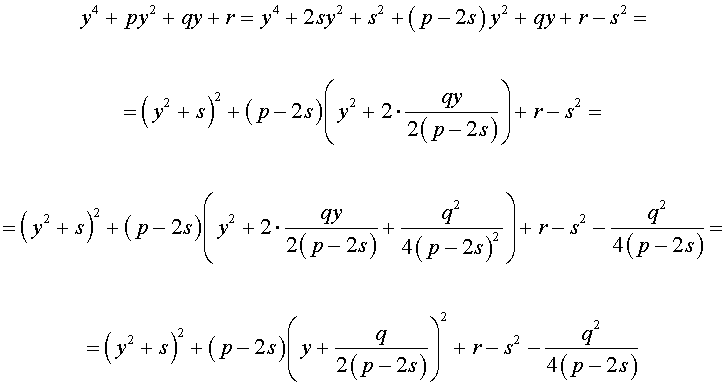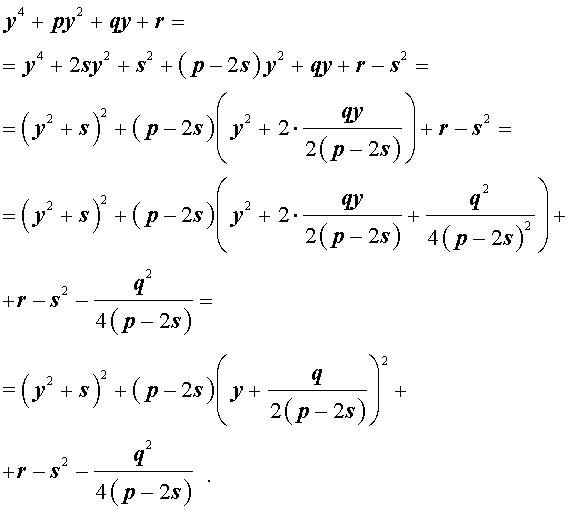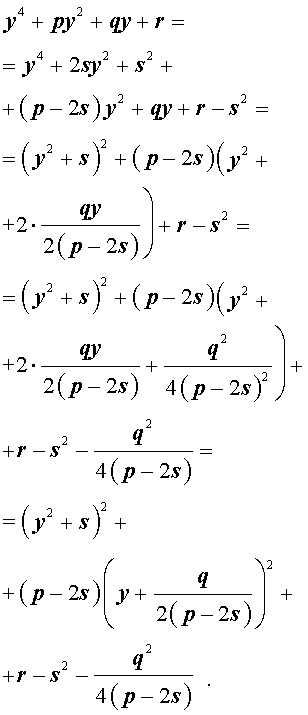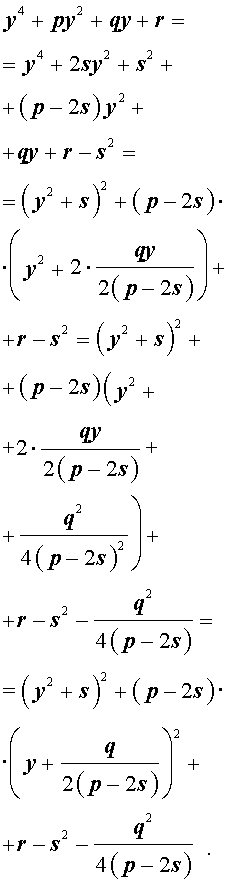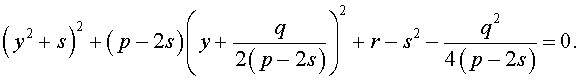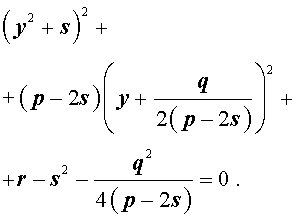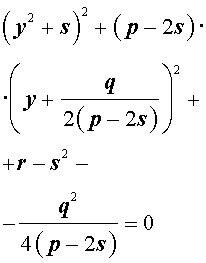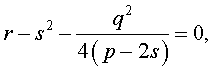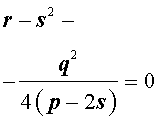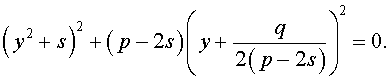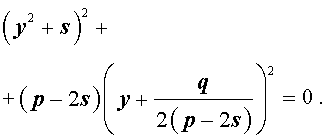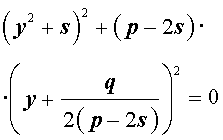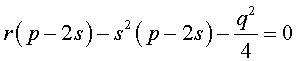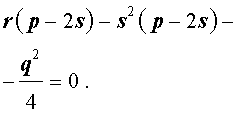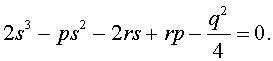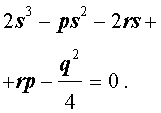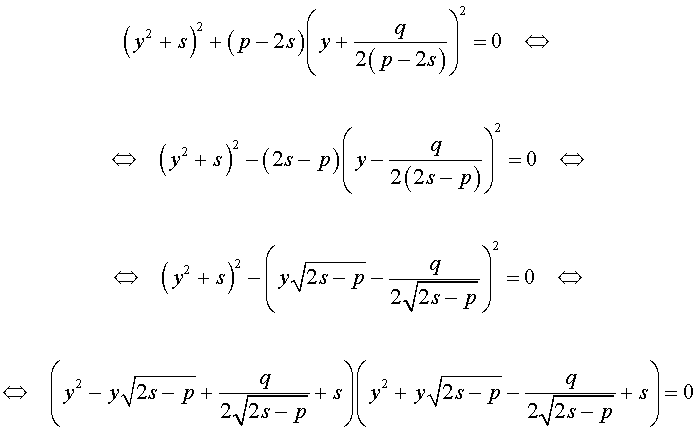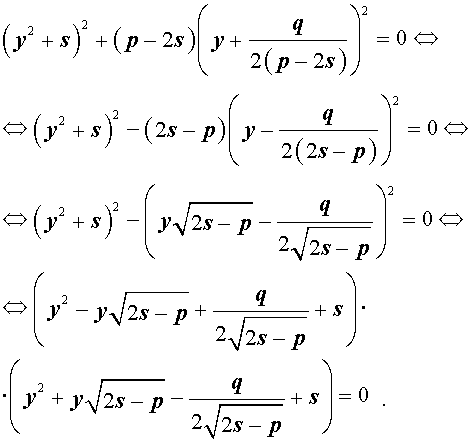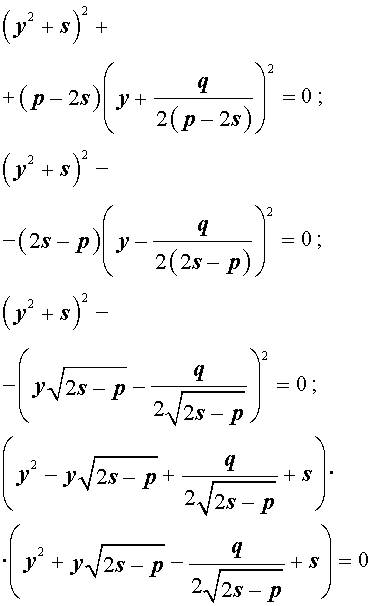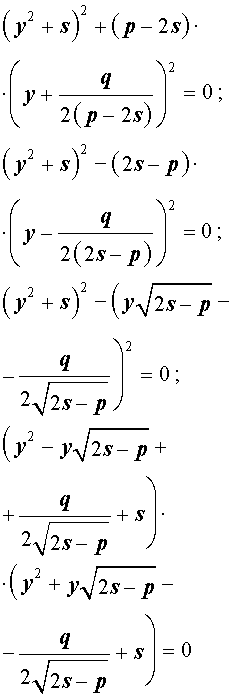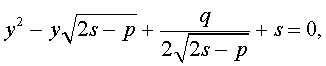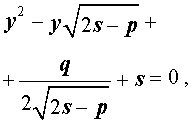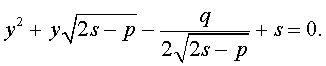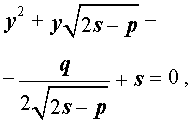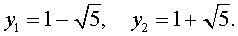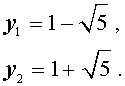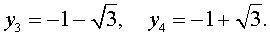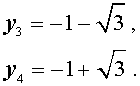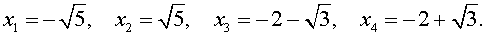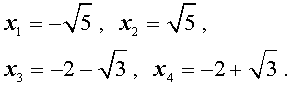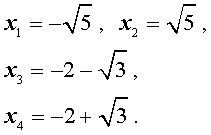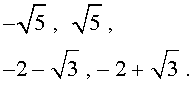Решение уравнений 4-ой степени. Метод Феррари
 Схема метода Феррари Схема метода Феррари |
 Приведение уравнений 4-ой степени Приведение уравнений 4-ой степени |
 Разложение на множители. Кубическая резольвента Разложение на множители. Кубическая резольвента |
 Пример решения уравнения 4-ой степени Пример решения уравнения 4-ой степени |
Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
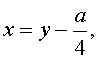 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
Как группировать уравнения с 4 степенью
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 — 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
Поэтому `p` может принимать значения:
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
в) Вынесем `x^2` за скобки и сгруппируем:
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
В итоге получаем:
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-chetvertoj-stepeni/
http://zftsh.online/articles/5013