Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными
Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными
Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»
Изображение на координатной плоскости множества решений уравнений и неравенств
с двумя переменными.
1. Изображение множества решений уравнений с двумя переменными.
Определение. Уравнение вида 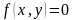
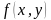
Решить уравнение – значит найти множество всех его корней.
Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.
Для того, чтобы решить уравнение с двумя переменными нужно построить его график.
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Задача 1. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения
Так как произведение равно нулю, то каждый из множителей также равен нулю.
Решим каждое из полученных уравнений:
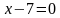
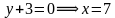
Решением является множество точек двух прямых: 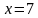
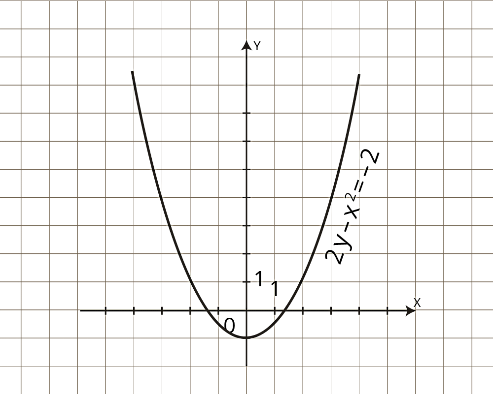
Задача 2. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения 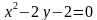
Для этого выразим переменную 
Уравнение задает параболу с вершиной в точке
То есть решением уравнения является множество точек параболы
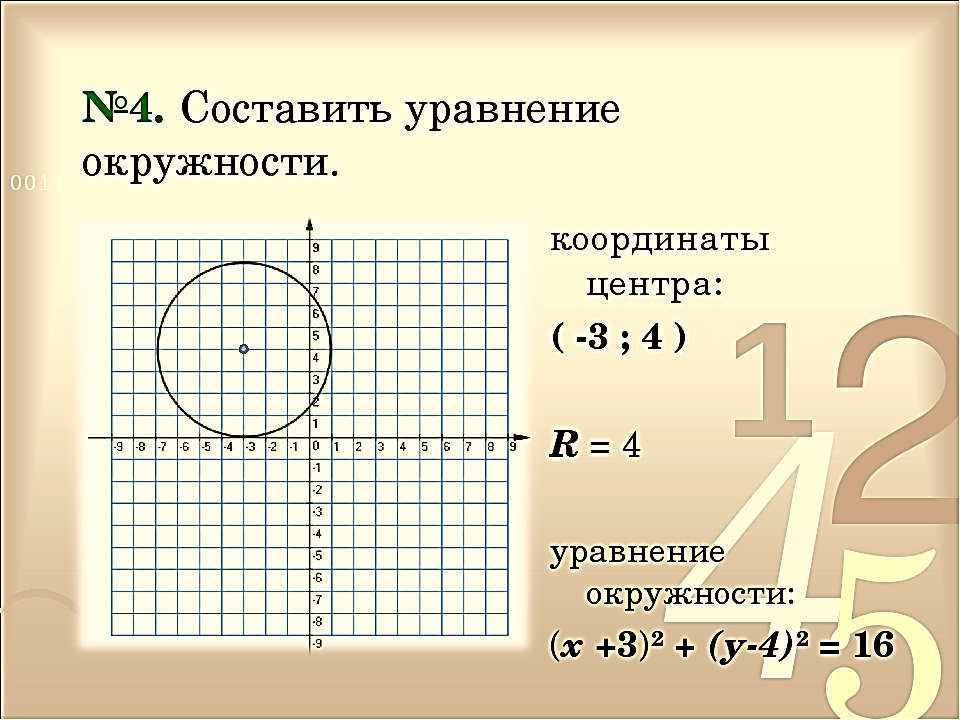
Задача 3. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения
Уравнение задает окружность с центром в точке 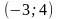
То есть решением уравнения является множество точек построенной окружности
2. Изображение множества решений неравенств с двумя переменными.
Определение. Выражение вида 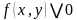
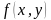
Решить неравенство – значит найти множество всех его решений.
Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.
Алгоритм решения неравенства
1. Построить график уравнения 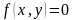
Если неравенство «строгое», тогда график изображаем пунктирной линией;
Если неравенство «нестрогое», тогда график изображаем сплошной линией.
2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.
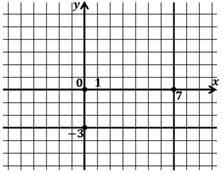
Задача 1. Изобразить на координатной плоскости множество решений неравенства
Построим график заданного неравенства . Для этого выразим переменную 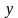
Уравнение задает линейную функцию, проходящую через точки:
Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.
Задача 2. Изобразить на координатной плоскости множество решений неравенства
Построим график заданного неравенства.
Уравнение задает параболу с вершиной в точке
Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.
Задача 3. Изобразить на координатной плоскости множество решений неравенства .
Графиком уравнения является гипербола .
Данная гипербола разбивает координатную плоскость на три области А, В и С.
Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.
Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.
Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.
Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.
3. Изображение множества решений системы неравенств с двумя переменными.
Решить систему неравенств – значит найти множество всех решений системы.
Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы
Задача 4. Изобразить на координатной плоскости множество решений системы неравенств
На координатной плоскости множество всех решений неравенства
изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).
Аналогично строим график неравенства .
То есть строим на координатной плоскости прямую
Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.
Задача 5. Изобразить на координатной плоскости множество решений системы неравенств
На координатной плоскости множество всех решений неравенства
изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.
Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Координатные плоскости и графики
Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.
Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость. В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости и ts-плоскости.
Упорядоченная пара
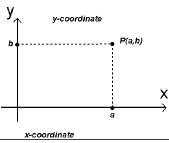
Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.
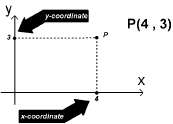
Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости
Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.
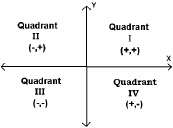
В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке
Определение графика
Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
http://www.math10.com/ru/algebra/grafiki/koordinatnie-ploskosti-i-grafiki.html

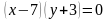
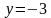
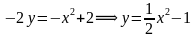
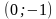
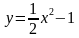
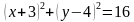
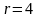






 при х ≠ -1.
при х ≠ -1.






 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0. , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b