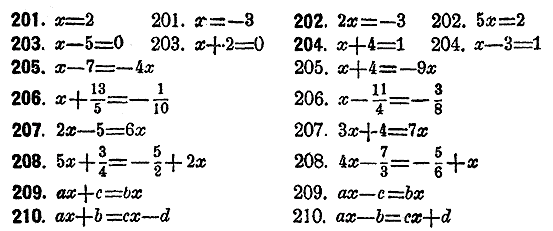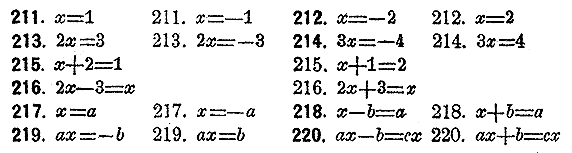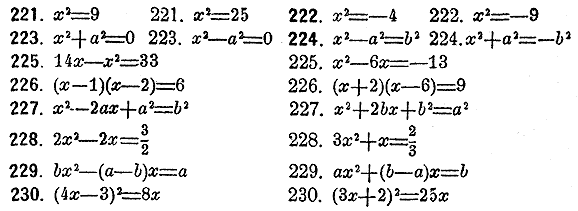Как извлечь квадратный корень из обеих частей уравнения

Как извлечь квадратный корень из обеих частей уравнения

УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.

§ 5. Возведение уравнений в степень и извлечение из них корня.

От возведения обеих частей уравнения в одну и ту же степень получается новое уравнение, вообще говоря, несовместное с прежним, потому что это новое уравнение удовлетворяется не только всеми корнями прежнего уравнения, но содержит еще лишние корни, принадлежащие особому уравнению, дополнительному к данному.

Так, если уравнeниe А=В возвeдем в квадрат, то получим новоe уравнeниe А 2 =В 2 , котороe можем замeнить через А 2 —В 2 =0, а послeднee разлагается на уравнeниe А—В=0, или А=:В (данное) и уравнениe А+В = 0, или А=—В (дополнитeльноe).

Если уравнeниe А=В возведeм в куб, то получим новое уравнeниe А 3 =В 3 , или
А 3 —В 3 = 0. Но послeднee, будучи написано в видe (А—В)(А 2 + АВ+ В 2 )=0, разлагается на уравнениe А—В=0, или А=В (данноe) и уравнение А 2 + АВ+ В 2 =0 (дополнительноe).

То жe замeчание относитея и к возведению в другие, высшие степени.

Возвести нижeуказанные уравнения в квадраты и опредeлить лишние, внeсенные этим дeйствием, рeшeния:

Возвести нижеуказанные уравнения в куб, опредeлить лишние рeшения и провeрить эти рeшeния подстановкой их в уравнения, получаемые от возвeдения в куб данных уравнeний:

Из вышeприведенной теоремы о возведении уравнeния в степень видно, что, при извлечении корня из обeих частей уравнeния, число рeшений этого уравнения уменьшается, и потому для восстановления общности данного уравнения нужно рссматривать нe только то уравневиe, котороe получаeтся из данного нeпосредствeнным извлeчeнием корня, но и уравнение, дополнительноe к получаемому.

Так, извлекая квадратный корень из уравнения А 2 =В 2 , нужно рассматривать не только уравнeние А=В, но и дополнительное к нему А = —В.

Извлекая кубический корeнь из уравнения А 3 =В 3 , нужно выражать рeшeниe уравнeнием А=В и eще дополнитeльным к нему уравнениeм А 2 + АВ+ В 2 = 0

То жe относится и к извлечeнию корнeй с высшими показателями.

Рeшить нижеслeдующия уравнения посрeдством извлeчeния квадратного корня:

Рeшить нижеслeдующие уравнения посредством извлечения кубического корня:

Основные методы решения уравнений

Что такое решение уравнения?

Тождественное преобразование. Основные

виды тождественных преобразований.

Посторонний корень. Потеря корня.

Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим уравнением, ему равносильным . Такая замена называется тождественным преобразованием . Основные тождественные преобразования следующие:

Замена одного выражения другим, тождественно равным ему. Например, уравнение ( 3x+ 2 ) 2 = 15x+10 можно заменить следующим равносильным: 9 x 2 + 12x + 4 = 15x + 10 .

Перенос членов уравнения из одной стороны в другую с обратными знаками. Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком « – »: 9 x 2 + 12x + 4 – 15x – 10 = 0, после чего полу чим: 9 x 2 – 3x – 6 = 0 .

Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Это очень важно, так как новое уравнение может не быть равносильным предыдущему, если выражение, на которое мы умножаем или делим, может быть равно нулю.

П р и м е р . Уравнение x – 1 = 0 имеет единственный корень x = 1.

Умножив обе его части на x – 3 , мы получим уравнение

( x – 1 )( x – 3 ) = 0, у которого два корня: x = 1 и x = 3.

Последнее значение не является корнем заданного уравнения

x – 1 = 0. Это так называемый посторонний корень.

И наоборот, деление может привести к потере корня. Так

в нашем случае, если ( x – 1 )( x – 3 ) = 0 является исходным

уравнением, то корень x = 3 будет потерян при делении

обеих частей уравнения на x – 3 .

В последнем уравнении (п.2) мы можем разделить все его члены на 3 (не ноль!) и окончательно получим:

Это уравнение равносильно исходному:

( 3x+ 2 ) 2 = 15x + 10 . 4.

Можно возвести обе части уравнения в нечётную степень или извлечь и з обеих частей уравнения корень нечётной степени . Необходимо помнить, что:

а) возведение в чётную степень может привести к приобретению посторонних корней ;

б) неправильное извлечение корня чётной степени может привести к потере корней.

П р и м е р ы . Уравнение 7 x = 35 имеет единственный корень x = 5 .

Возведя обе части этого уравнения в квадрат, получим

имеющее два корня: x = 5 и x = – 5. Последнее значение

является посторонним корнем.

Неправильное извлечение квадратного корня из обеих

частей уравнения 49 x 2 = 1225 даёт в результате 7 x = 35,

и мы теряем корень x = – 5.

Правильное извлечение квадратного корня приводит к

уравнению: | 7 x | = 35, а следовательно, к двум случаям:

1) 7 x = 35, тогда x = 5 ; 2) – 7 x = 35, тогда x = – 5 .

Следовательно, при правильном извлечении квадратного

корня мы не теряем корней уравнения.

Что значит правильно извлечь корень? Здесь мы встречаемся

с очень важным понятием арифметического корня

Copyright © 2004 — 2012 Др. Юрий Беренгард. All rights reserved.

Как извлечь квадратный корень из обеих частей уравнения

Ключевые слова: решение уравнения, тождественное преобразование, тождественные преобразования, посторонний корень, потеря корня.

Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим уравнением, ему равносильным . Такая замена называется тождественным преобразованием .

Основные тождественные преобразования:

Замена одного выражения другим, тождественно равным ему. Например, уравнение ( 3x+ 2 ) 2 = 15x+10 можно заменить следующим равносильным: 9x 2 + 12x + 4 = 15x + 10

Перенос членов уравнения из одной стороны в другую с обратными знаками. Так, в предыдущем уравнении мы можем перенести все его члены из правой части в левую со знаком « – »: 9x 2 + 12x + 4 – 15x – 10 = 0, после чего полу чим: 9x 2 – 3x – 6 = 0 .

Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Это очень важно, так как новое уравнение может не быть равносильным предыдущему, если выражение, на которое мы умножаем или делим, может быть равно нулю. Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение ( x – 1 )( x – 3 ) = 0, у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление может привести к потере корня. Так, если ( x – 1 )( x – 3 ) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x – 3 .

Можно возвести обе части уравнения в нечетную степень или извлечь и з обеих частей уравнения корень нечетной степени . Необходимо помнить, что: а) возведение в четную степень может привести к приобретению посторонних корней ; б) неправильное извлечение корня четной степени может привести к потере корней.

Уравнение 7 x = 35 имеет единственный корень x = 5 . Возведя обе части этого уравнения в квадрат, получим уравнение: 49 x 2 = 1225 ,
имеющее два корня: x = 5 и x = – 5. Последнее значение является посторонним корнем. Неправильное извлечение квадратного корня из обеих
частей уравнения 49 x 2 = 1225 даёт в результате 7 x = 35,и мы теряем корень x = – 5. Правильное извлечение квадратного корня приводит к
уравнению: | 7 x | = 35, а следовательно, к двум случаям: 1) 7 x = 35, тогда x = 5 ; 2) – 7 x = 35, тогда x = – 5 .Следовательно, при правильном извлечении квадратного корня мы не теряем корней уравнения.

Пример. Решите уравнение $$\sqrt-x> + \sqrt<2 - x - x^<2>> = \sqrt — 1$$

Решение. В этом примере наоборот сложно его решение. Однако поиск ОДЗ приносит несомненную пользу.
В самом деле, ОДЗ: $$\left\< \begin
x^2 — x \ge 0 \\
2 — x — x^2 \ge 0 \\
x \ge 0
\end \right.\, \Leftrightarrow \left\< \begin
x \in \left( < - \infty ;0>\right] \cup \left[ <1; + \infty >\right) \\
x \in \left[ < - 2;1>\right] \\
x \in \left[ <0; + \infty >\right)
\end \right.\, \Leftrightarrow \left[ \begin
x = 0 \\
x = 1
\end \right.$$

Значит, ОДЗ нашего уравнения содержит только два числа. А поскольку вне ОДЗ решений быть не может, то корнями нашего уравнения могут быть только эти два числа. Для того чтобы понять, какое из них действительно является решением, нужно полученные числа подставить в уравнение. Подстановка даёт, что x = 0 не является решением уравнения, а x = 1 − является.

Ответ. 1.

Таким образом, к понятию ОДЗ нужно относиться творчески и искать его, только если в этом возникает существенная необходимость. Так, например, в равносильном переходе $$\sqrt = g(x)\, \Leftrightarrow \left\< \begin
g(x) \ge 0, \\
f(x) = g^2 (x)
\end \right.$$

требование g ( x ) ? 0 задает ОДЗ. Однако, если искать g ( x ) очень сложно, то проще подставить найденные корни в исходное уравнение, чем выяснять, при каких x выполнено неравенство g ( x ) ? 0.