Как находить промежутки знакопостоянства функции по уравнению

Свойства функции

В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое числовая функция и какие свойства функции необходимо знать и уметь исследовать.

Что такое числовая функция? Пусть у нас есть два числовых множества: Х и Y, и между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие единственный элемент y из множества Y.

Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.

Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.

Множество Х называется областью определения функции.

Множество Y называется множеством значений значений функции.

Равенство называется уравнением функции. В этом уравнении — независимая переменная, или аргумент функции. — зависимая переменная.

Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.

Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.

Основные свойства функций.

1. Область определения функции.

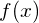
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции имеет смысл. Другими словами, это область допустимых значений выражения .

Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.

2. Множество значений функции.

Множество значений функции Е(y)— это множество всех значений, которые может принимать зависимая переменная y.

Чтобы по графику функции найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.

Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.

Чтобы найти нули функции , нужно решить уравнение . Корни этого уравнения и будут нулями функции .

Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции .

4. Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть или .

Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и .

Чтобы найти промежутки знакопостоянства функции по ее графику, нужно

найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента ,
найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента .

5. Промежутки монотонности функции.

Промежутки монотонности функции — это такие промежутки значений аргумента х, при которых функция возрастает или убывает.

Говорят, что функция возрастает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .

Другими словами, функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.

Говорят, что функция убывает на промежутке I, если для любых двух значений аргумента , принадлежащих промежутку I таких, что выполняется соотношение: .

Другими словами, функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.

6. Точки максимума и минимума функции.

Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой x_0 лежит выше других точек из окрестности I графика функции y=f(x).

Точка называется точкой минимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой лежит ниже других точек из окрестности I графика функции .

Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.

7. Четность (нечетность) функции.

Функция называется четной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.

Другими словами, область определения четной функции симметрична относительно начала координат.

б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Функция называется нечетной, если выполняются два условия:

Другими словами, область определения нечетной функции симметрична относительно начала координат.

б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.

Чтобы определить четность функции, нужно:

а). Найти область определения функции , и определить, является ли она симметричным множеством.

Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.

Если область определения функции — симметричное множество, то проверяем п. б)

б). В уравнение функции нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду или .

Если , то функция четная.

Если , то функция нечетная.

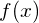
Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.

График четной функции симметричен относительно оси ординат ( прямой OY ).

График нечетной функции симметричен относительно начала координат ( точки (0,0) ).

8. Периодичность функции.

Функция называется периодической, если существует такое положительное число Т, что

для любого значения х из области определения функции, х+Т также принадлежит D(x)

В программе средней школы из числа периодических функций изучают только тригонометрические функции.

Предлагаю вам посмотреть ВИДЕОУРОК, в котором я рассказываю, как определить свойства функции по ее графику.

Свойства функций: чётность, промежутки знакопостоянства, монотонность.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь рассмотрим свойства функций. Их существует много, однако, изучаются они постепенно. В 9 классе мы знакомимся с нулями функции, промежутками возрастания и убывания (монотонность) и промежутками знакопостоянства и чётностью (нечётностью) функции. Рассмотрим их подробно.

Нулями функции называются значения независимой переменной (аргумента), при которых значение функции равно нулю. В графической интерпретации нулями функции являются абсциссы точек пересечения графика с осью абсцисс (осью х).

На графике нули функции: .

Для того, чтобы найти нули функции, заданной аналитически, необходимо решить уравнение: . Корни этого уравнения являются нулями функции.

Например, найти нули функции .

Промежутками знакопостоянства функции называются промежутки значений аргумента, на которых значения функции либо только положительны, либо только отрицательны. Другими словами, это те промежутки, на которых функция сохраняет свой знак.

Рассматривая график сверху, найдём промежутки знакопостоянства.

функция принимает только положительные значения на тех участках графика, где он находится выше оси Ох, т.е. при ;

функция принимает только отрицательные значения на тех участках графика, где он находится ниже оси Ох, т.е. при .

Для того, чтобы найти промежутки знакопостоянства функции, заданной аналитически, необходимо решить неравенства: и . Решения этих неравенств и будут промежутками знакопостоянства функции.

Например, найти промежутки знакопостоянства функции .

Это неравенство можно решить двумя способами: с помощью систем неравенств и методом интервалов. Метод интервалов будет рассмотрен нами чуть позже, поэтому воспользуемся системами неравенств. Произведение двух множителей положительно, если эти множители имеют одинаковый знак. Значит, получается совокупность двух систем:

Теперь находим промежутки, на которых функция принимает отрицательные значения.

Произведение двух множителей отрицательно, если эти множители имеют разные знаки, т.е.

Чётной называется функция, если противоположным значениям аргумента соответствуют одинаковые значения функции, т.е. . График чётной функции симметричен относительно оси ординат (оси Оу).

Нечётной называется функция, если противоположным значениям аргумента соответствуют противоположные значения функции, т.е. . График нечётной функции симметричен относительно начала координат.

На рисунке слева график чётной функции, на рисунке справа – нечётной функции.

Для того, чтобы определить чётность функции, заданной аналитически, необходимо в заданную функцию вместо х подставить –х и произвести упрощение. Если в результате получится функция, равная заданной, то функция чётная; если получится функция, противоположная заданной, то она нечётная; если не получится ни один из предложенных вариантов, то функция не является ни чётной, ни нечётной.

Например, исследовать на чётность функцию .

Находим значение этой функции при противоположном значении х, т.е.

Полученное выражение не совпадает с заданным и не противоположно ему, значит, функция не является ни чётной, ни нечётной. Её график не симметричен относительно оси Оу и не симметричен относительно начала координат.

Приведём ещё один пример: .

После упрощения получили выражение, полностью совпадающее с заданным. Значит, функция является чётной и её график симметричен относительно начала координат.

Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции (или меньшему значению аргумента соответствует меньшее значение функции), т.е. если при , то функция возрастающая.

Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции (или меньшему значению аргумента соответствует большее значение функции), т.е. если при , то функция убывающая.

Для примера рассмотрим графики на рисунках выше.

Синий график: функция возрастает при

функция убывает при

Зелёный график: функция возрастает при

функция убывает при

Промежутки возрастания и убывания функции называются промежутками монотонности функции.

Если функция задана аналитически, то нахождение промежутков монотонности является более сложным процессом и он изучается в 11 классе. Мы ограничимся определением этих промежутков по графикам.

Наибольшим значением функции называется самое большое значение функции по сравнению со всеми остальными.

Наименьшим значением функции называется самое маленькое значение функции по сравнению со всеми остальными.

Строгое определение наибольшего и наименьшего значения функции будет дано в старших классах.

На синем графике наибольшего значения нет, т.к. график бесконечен в положительном направлении оси Оу. А наименьшее значение равно . Записывается это так: .

На зелёном графике нет ни наибольшего, ни наименьшего значения функции.

На рисунках изображены части графиков нечётных функций. Достройте эти графики.

Какая из данных функций является чётной, а какая – нечётной:

Приведите необходимые обоснования.

Докажите, что – чётная функция, а – нечётная, если:

Является ли чётной или нечётной функция , если:

На рисунках изображены части графиков чётных функций. Достройте эти графики.

Постройте график функции , зная, что при её значения могут быть найдены по формуле:

Известно, что функция – чётная и она обращается в нуль при и . Укажите другие значения аргумента, при которых .

Известно, что функция – чётная и она принимает значения, равные нулю, при и . Укажите другие значения аргумента, при которых .

Известно, что уравнение , где – нечётная функция с областью определения , имеет положительные корни и . Найдите неположительные корни уравнения.

Линейная функция является нечётной. Найдите значение .

Функция , где – некоторое число, является чётной. Найдите значение .

Известно, что и – нечётные функции. Верно ли утверждение, что нечётной является функция , если:

Известно, что и – нечётные функции. Верно ли утверждение, что чётной является функция , если: Представьте каким-либо способом функцию в виде суммы чётной и нечётной функций, если:

Функция , область определения которой – промежуток , задана графиком на рисунке. Укажите промежутки, на которых эта функция возрастает и на которых убывает.

Какая из линейных функций и является возрастающей, убывающей и почему?

Докажите, что функция является убывающей на промежутке и возрастающей на промежутке .

Докажите, что функция является возрастающей на промежутке и убывающей на промежутке .

Укажите промежутки возрастания и убывания функций .

Определите характер монотонности функций и . Докажите, что функция возрастающая, а функция — убывающая.

Известно, что функция является монотонной и что уравнение имеет корень, равный . Имеет ли это уравнение другие корни?

Известно, что уравнение , где – монотонная функция, имеет корень, равный . Имеет ли это уравнение другие корни?

Известно, что функция возрастает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство:

Известно, что функция убывает на промежутке . При каких значениях, принадлежащих этому промежутку, верно неравенство: Известно, что функции и – убывающие. Является ли убывающей функция , если: Известно, что функции и – возрастающие. Является ли возрастающей функция , если: Известно, что функция определена на множестве и возрастает на промежутке , где . Как изменяется эта функция на промежутке , если:

Известно, что функция определена на множестве и убывает на промежутке , где . Как изменяется эта функция на промежутке , если:

Найдите наибольшее и наименьшее значения функции:

Укажите значение аргумента, при котором функция принимает наименьшее значение. Существует ли наибольшее значение этой функции?

Укажите значение аргумента, при котором функция принимает наибольшее значение. Существует ли наименьшее значение этой функции?

Найдите область определения функции:

Найдите нули функции и области положительных и отрицательных значений, если:

Изобразите схематически график функции , зная результаты исследования функции:

функция является непрерывной и нечётной;

функция возрастает на промежутке .

Изобразите схематически график функции , зная результаты исследования функции:

функция является непрерывной и чётной;

функция возрастает на промежутке .

С помощью графика определите свойства функции:

область определения функции;

область значений функции;

монотонность функции (промежутки возрастания и убывания);

наибольшее и наименьшее значение функции.

Определить свойства функций, заданных формулами:

С помощью графика определите свойства функции:

область определения функции;

область значений функции;

монотонность функции (промежутки возрастания и убывания);

наибольшее и наименьшее значение функции.

Найдите нули функции (если они существуют):

С помощью графика определите свойства функции:

область определения функции;

область значений функции;

монотонность функции (промежутки возрастания и убывания);

наибольшее и наименьшее значение функции.

Постройте график функции и опишите её свойства.

Выясните свойства функции

С помощью графика определите свойства функции:

область определения функции;

область значений функции;

монотонность функции (промежутки возрастания и убывания);

наибольшее и наименьшее значение функции.

Дана функция . При каких значениях аргумента ? Является ли эта функция возрастающей или убывающей?

Краткое описание документа:

Данная разработка знакомит учеников 9 класса с базовыми свойствами функций: нулями функции, промежутками знакопостоянства, промежутками монотонности, чётностью и нечётностью функции, наибольшим и наименьшим значением функции. В теоретической части представлены определения, примеры, иллюстрации. Практическая часть разработки содержит большой объём заданий разного уровня сложности.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 920 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 585 012 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

2. Свойства функций

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

30.09.2019
230
3

19.09.2019
1341
17

18.09.2019
834
38

14.09.2019
237
14

24.08.2019
986
42

24.08.2019
1109
10

16.08.2019
1013
44

27.02.2019
434
4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

04.10.2019 4100
DOCX 516.6 кбайт
18 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Колесник Марина Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 3 года и 11 месяцев
Подписчики: 0
Всего просмотров: 266286
Всего материалов: 132

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.

теория по математике 📈 функции

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

График функции у=k/x выглядит следующим образом: 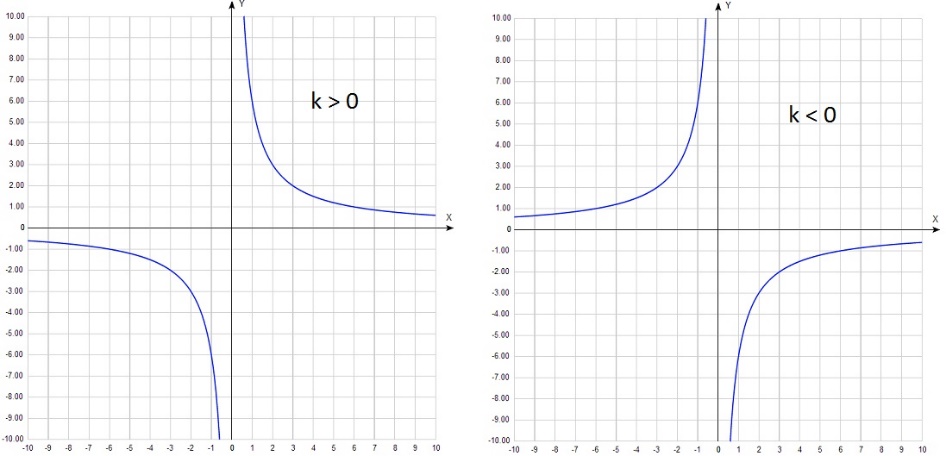По данному рисунку видно, что нулей функции не существует. Как найти нули функции?

Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

источники:

http://infourok.ru/svoystva-funkciy-chyotnost-promezhutki-znakopostoyanstva-monotonnost-3866952.html

http://spadilo.ru/svojstva-funkcii/