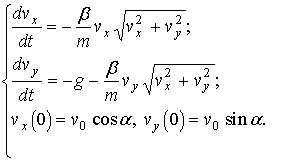Как написать программу для решения дифференциальных уравнений

Как написать программу решения дифференциального уравнения… ( C++ )

Для численного решения обыкновенных дифференциальных уравнений различают задачи с начальными условиями (ЗНУ) и граничными условиями (ЗГУ).

Дело в том, что для полного определения искомой функции одного уравнения недостаточно. При определении первообразной из производной функции мы получим множество решений, отличающихся друг от друга свободным членом (константой С).

Поэтому, для однозначного определения данной константы С, у искомой функции должны задаваться еще граничные условия, указывающие, что делается на концах исследуемого интервала, и/или начальные условия, описывающие значение функции
в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.

Для численного решения обыкновенных дифференциальных уравнений применяют метод Рунге-Кутта, с наиболее часто используемым 4-ым порядком точности. Давайте рассмотрим программную реализацию данного метода Рунге-Кутта, и Вы увидите, что написать программу для решения дифференциального уравнения не составляет особого труда.

Вариант решения задачи рассмотрю на следующем примере:

Условия задачи:
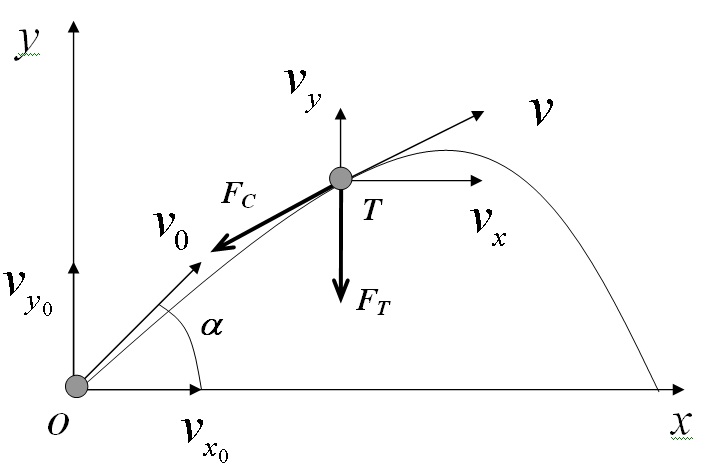
Пусть выстрел из орудия произведен с начальной скоростью V₀, под углом к горизонту α, с высоты Н₀ расположения орудия, т.к. в реальности огонь может вестись с холма или из капонира (т.е. ниже уровня земли).
Считаем, что снаряд имеет форму шара с радиусом r, изготовлен из материала, имеющего определенную плотность ρ.
Построить траекторию полета снаряда Y(x) ,
указать максимальную высоту полета H_k , дальность падения снаряда X_k и время полета t_k , построить график скорости V(t) на отрезке [0,t_k].

Таким образом, исходные данные, которые пользователь может задать на форме:
Начальная скорость V₀, м/с2
Начальная высота H₀, м
Угол выстрела α, ° (град)
Плотность материала ρ, кг/м3
Радиус r, м

При построении математической модели условимся, что ось Оx системы координат направлена горизонтально в направлении выстрела, а ось Oy — вертикально вверх. Вектор скорости снаряда V(t) за время полета будет изменяться как по величине, так и по направлению, поэтому в модели рассматриваем его проекции на координатные оси. Горизонтальную составляющую скорости в момент времени t обозначим V_x(t), а вертикальную – V_y(t).

Пусть поверхность Земли плоская. Согласно законам механики, при сделанных предположениях движения тела в горизонтальном направлении является равномерным, а в вертикальном – равнозамедленным или равноускоренным с ускорением свободного падения g.

Если с силой тяжести F_T все достаточно просто (она свой вектор не меняет ни по величине, ни по направлению), то сила лобового сопротивления F_C , действующая на снаряд, пропорциональна квадрату скорости движения тела. Обозначим через F_X и F_Y горизонтальную и вертикальную проекции вектора силы лобового сопротивления,
причем F_X/F= V_X/V, F_Y/F= V_Y/V.

Значение силы лобового сопротивления F= -b·V² (пропорционально квадрату скорости тела). Коэффициент b=0.5·C·S·ρ, где C – коэффициент лобового сопротивления (для многих задач баллистики C≈0.15), S – площадь поперечного сечения (S=πr²), ρ — плотность воздуха (ρ=1,29 кг/м3).

Решение поставленной задачи можно свести к решению системы дифференциальных уравнений

Метод Рунге-Кутта предполагает многократное вычисление значения производной искомой функции по имеющейся формуле (из уравнения), поэтому имеет смысл …

Код функций будет выглядеть так:

// функция Нахождение горизонтальной проекции скорости
//по первому уравнению системы
double Form1::fvx( double vy, double vx )
<
return -b*vx*sqrt(vx*vx+vy*vy) / m;
>

// функция Нахождение вертикальной проекции скорости
//по второму уравнению системы
double Form1::fvy( double vy, double vx )
<
return -b*vy*sqrt(vx*vx+vy*vy) / m — g;
>

Шаг интегрирования у меня задается на форме.
Сейчас нам предстоит вычислить значения нескольких функций (V_x, V_y, V ) в точках интервала с шагом. В моем примере у интервала задано начало х=0, а конечная точка интервала будет определена в процессе вычисления ( высота полета ядра стала Void Form1::Runge_Kutta(void)
<
double k1,k2,k3,k4, l1,l2,l3,l4;

pY[0]=H; pX[0]=0; pt[0]=0; //массивы-координаты: высота, дальность и время
pVx[0]=Vx; pVy[0]=Vy; pV[0]=V; //массивы- скорости: проекции на
//горизонталь и вертикаль и полная скорость (величина вектора)
bool vzbool=true;//взлет
int i=1;

//расчет по модели и заполнение массивов
while( (pY[i-1]>-0.00001 || vzbool) && i pY[i-1]) iMax=i; //сохранение номера узла с максимальной высотой
else vzbool=false;//падение

i++;
>
n=i-1; //количество реальных шагов
>

где:
int iMax; //узел с макс.высотой полета

double b; //коэф.пропорциональности Силы лобового сопротивления
double m; //масса ядра
double H; //уровень расположения орудия в момент выстрела
double V,Vx,Vy; //начальная скорость и ее проекции на оси

В результате работы этой подпрограммы произойдет численное решение задачи Коши для системы обыкновенных дифференциальных уравнений и будут получены значения функций V_x(t_i), V_y(t_i) в точках t_i=i·h, i=1,2. ; h – шаг метода.

Как видим, после получения нового значения скорости V_x(t_i)
рассчитывается координата X(t_i)=X(t_i-1)+h·V_x(t_i), где h= t_i-t_i-1 = const.
Кроме того, параллельно рассчитывается значение высоты Y(t_i)=Y(t_i-1)+h·V_y(t_i),
где h= t_i-t_i-1 = const по найденным значениям V_y(t_i).
Когда будет получено значение Y(t_i)

Символьное решение линейных дифференциальных уравнений и систем методом преобразований Лапласа c применением SymPy

Реализация алгоритмов на языке Python с использованием символьных вычислений очень удобна при решении задач математического моделирования объектов, заданных дифференциальными уравнениями. Для решения таких уравнений широко используются преобразования Лапласа, которые, говоря упрощенно, позволяют свести задачу к решению простейших алгебраических уравнений.

В данной публикации предлагаю рассмотреть функции прямого и обратного преобразования Лапласа из библиотеки SymPy, которые позволяют использовать метод Лапласа для решения дифференциальных уравнений и систем средствами Python.

Сам метод Лапласа и его преимущества при решении линейных дифференциальных уравнений и систем широко освещены в литературе, например в популярном издании [1]. В книге метод Лапласа приведен для реализации в лицензионных программных пакетах Mathematica, Maple и MATLAB (что подразумевает приобретение учебным заведением этого ПО) на выбранных автором отдельных примерах.

Попробуем сегодня рассмотреть не отдельный пример решения учебной задачи средствами Python, а общий метод решения линейных дифференциальных уравнений и систем с использованием функций прямого и обратного преобразования Лапласа. При этом сохраним обучающий момент: левая часть линейного дифференциального уравнения с условиями Коши будет формироваться самим студентом, а рутинная часть задачи, состоящая в прямом преобразовании Лапласа правой части уравнения, будет выполняться при помощи функции laplace_transform().

История об авторстве преобразований Лапласа

Преобразования Лапласа (изображения по Лапласу) имеют интересную историю. Впервые интеграл в определении преобразования Лапласа появился в одной из работ Л. Эйлера. Однако в математике общепринято называть методику или теорему именем того математика, который открыл ее после Эйлера. В противном случае существовало бы несколько сотен различных теорем Эйлера.

В данном случае следующим после Эйлера был французский математик Пьер Симон де Лаплас (Pierre Simon de Laplace (1749-1827)). Именно он использовал такие интегралы в своей работе по теории вероятностей. Самим Лапласом не применялись так называемые «операционные методы» для нахождения решений дифференциальных уравнений, основанные на преобразованиях Лапласа (изображениях по Лапласу). Эти методы в действительности были обнаружены и популяризировались инженерами-практиками, особенно английским инженером-электриком Оливером Хевисайдом (1850-1925). Задолго до того, как была строго доказана справедливость этих методов, операционное исчисление успешно и широко применялось, хотя его законность ставилось в значительной мере под сомнение даже в начале XX столетия, и по этой теме велись весьма ожесточенные дебаты.

Функции прямого и обратного преобразования Лапласа

Эта функция возвращает (F, a, cond), где F(s) есть преобразование Лапласа функции f(t), a Текст программы

Время на обратное визуальное преобразование Лапласа: 2.68 s

Обратное преобразование Лапласа часто используется при синтезе САУ, где Python может заменить дорогостоящих программных “монстров” типа MathCAD, поэтому приведенное использование обратного преобразования имеет практическое значение.

Преобразование Лапласа от производных высших порядков для решения задачи Коши

Если a и b — константы, то

для всех s, таких, что существуют оба преобразования Лапласа (изображения по Лапласу) функций f(t) и q(t).

Проверим линейность прямого и обратного преобразований Лапласа с помощью ранее рассмотренных функций laplace_transform() и inverse_laplace_transform(). Для этого в качестве примера примем f(t)=sin(3t), q(t)=cos(7t), a=5, b=7 и используем следующую программу.

(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
True
5*sin(3*t) + 7*cos(7*t)
5*sin(3*t) + 7*cos(7*t)

Приведенный код также демонстрирует однозначность обратного преобразования Лапласа.

Если предположить, что удовлетворяет условиям первой теоремы, то из этой теоремы будет следовать, что:

Повторение этого вычисления дает

После конечного числа таких шагов мы получаем следующее обобщение первой теоремы:

Применяя соотношение (3), содержащее преобразованные по Лапласу производные искомой функции с начальными условиями, к уравнению (1), можно получить его решение по методу, специально разработанному на нашей кафедре при активной поддержке Scorobey для библиотеки SymPy.

Метод решения линейных дифференциальных уравнений и систем уравнений, основанный на преобразованиях Лапласа, с использованием библиотеки SymPy

где — приведенное начальное положение массы, — приведенная начальная скорость массы.

Упрощённая физическая модель, заданная уравнением (4) при ненулевых начальных условиях [1]:

Система, состоящая из материальной точки заданной массы, закрепленной на пружине, удовлетворяет задаче Коши (задаче с начальными условиями). Материальная точка заданной массы первоначально находится в покое в положении ее равновесия.

Для решения этого и других линейных дифференциальных уравнений методом преобразований Лапласа удобно пользоваться следующей системой, полученной из соотношений (3):

Последовательность решения средствами SymPy следующая:

загружаем необходимые модули и явно определяем символьные переменные:

указываем версию библиотеки sympy, чтобы учесть ее особенности. Для этого нужно ввести такие строки:

по физическому смыслу задачи переменная времени определяется для области, включающей ноль и положительные числа. Задаём начальные условия и функцию в правой части уравнения (4) с её последующим преобразование по Лапласу. Для начальных условий необходимо использовать функцию Rational, поскольку использование десятичного округления приводит к ошибке.

пользуясь (5), переписываем преобразованные по Лапласу производные, входящие в левую часть уравнения (4), формируя из них левую часть этого уравнения, и сравниваем результат с правой его частью:

решаем полученное алгебраическое уравнение относительно преобразования X(s) и выполняем обратное преобразование Лапласа:

осуществляем переход из работы в библиотеке SymPyв библиотеку NumPy:

строим график обычным для Python методом:

Получаем:
Версия библиотеки sympy – 1.3

Получен график периодической функции, дающей положение материальной точки заданной массы. Метод преобразования Лапласа с использованием библиотеки SymPy дает решение не только без потребности сначала найти общее решение однородного уравнения и частное решение первоначального неоднородного дифференциального уравнения, но и без потребности использования метода элементарных дробей и таблиц Лапласа.

При этом учебное значение метода решения сохраняется за счёт необходимости использования системы (5) и перехода в NumPy для исследования решения более производительными методами.

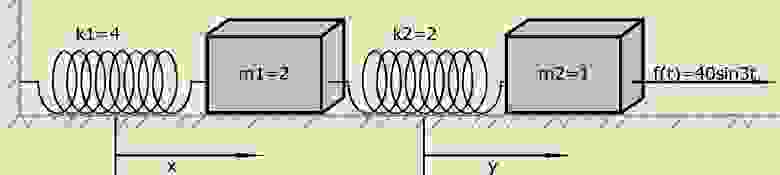
Для дальнейшей демонстрации метода решим систему дифференциальных уравнений:

с начальными условиями

Упрощённая физическая модель, заданная системой уравнений (6) при нулевых начальных условиях:

Таким образом, сила f(t) внезапно прилагается ко второй материальной точке заданной массы в момент времени t = 0, когда система находится в покое в ее положении равновесия.

Решение системы уравнений идентично ранее рассмотренному решению дифференциального уравнения (4), поэтому привожу текст программы без пояснений.

Для ненулевых начальных условий текст программы и график функций примет вид:

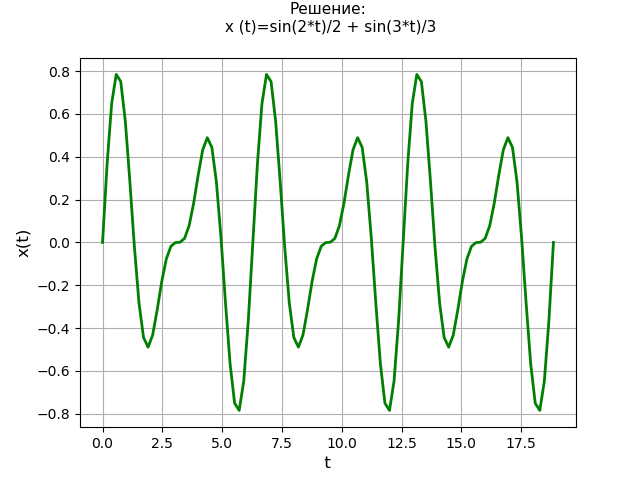
Рассмотрим решение линейного дифференциального уравнения четвёртого порядка с нулевыми начальными условиями:

Решим линейное дифференциальное уравнение четвёртого порядка:

с начальными условиями , , .

Функции для решения ОДУ

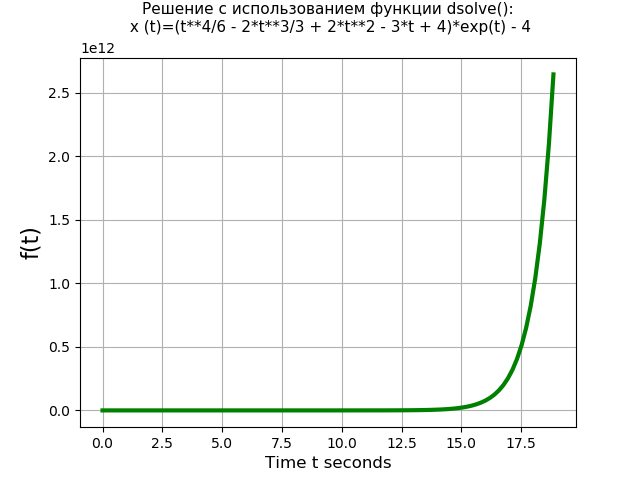
Для имеющих аналитическое решение ОДУ и систем ОДУ применяется функция dsolve():
sympy.solvers.ode.dsolve(eq, func=None, hint=’default’, simplify=True, ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)

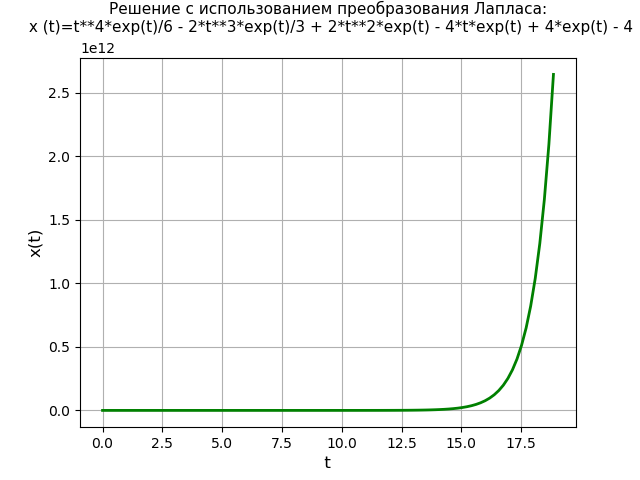
Давайте сравним производительность функции dsolve() с методом Лапласа. Для примера возьмём следующее дифференциальное уравнение четвёртой степени с нулевыми начальными условиями:

Время решения уравнения с использованием функции dsolve(): 1.437 s

Время решения уравнения с использованием преобразования Лапласа: 3.274 s

Итак, функция dsolve() (1.437 s) решает уравнение четвёртого порядка быстрее, чем выполняется решение по методу преобразований Лапласа (3.274 s) более чем в два раза. Однако при этом следует отметить, что функция dsolve() не решает системы дифференциальных уравнений второго порядка, например, при решении системы (6) с использованием функция dsolve() возникает ошибка:

Данная ошибка означает, что решение системы дифференциальных уравнений с помощью функции dsolve() не может быть представлено символьно. Тогда как при помощи преобразований Лапласа мы получили символьное представление решения, и это доказывает эффективность предложенного метода.

Для того чтобы найти необходимый метод решения дифференциальных уравнений с помощью функции dsolve(), нужно использовать classify_ode(eq, f(x)), например:

Eq(f(x), C1*sin(x) + C2*cos(x))
(‘nth_linear_constant_coeff_homogeneous’, ‘2nd_power_series_ordinary’)
(‘separable’, ‘1st_exact’, ‘almost_linear’, ‘1st_power_series’, ‘lie_group’, ‘separable_Integral’, ‘1st_exact_Integral’, ‘almost_linear_Integral’)
[Eq(f(x), -acos((C1 + Integral(0, x))*exp(-Integral(-tan(x), x))) + 2*pi), Eq(f(x), acos((C1 + Integral(0,x))*exp(-Integral(-tan(x), x))))]

Таким образом, для уравнения eq=Eq(f(x).diff(x,x)+f(x),0) работает любой метод из первого списка:

Для уравнения eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) работает любой метод из второго списка:

separable, 1st_exact, almost_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral

Чтобы использовать выбранный метод, запись функции dsolve() примет вид, к примеру:

Вывод:

Данная статья ставила своей целью показать, как использовать средства библиотек SciPy и NumPy на примере решения систем линейных ОДУ операторным методом. Таким образом, были рассмотрены методы символьного решения линейных дифференциальных уравнений и систем уравнений методом Лапласа. Проведен анализ производительности этого метода и методов, реализованных в функции dsolve().

1. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
2. Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке \( t = 0 \) необходимо найти из уравнения (3) решение при других \( t \).

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_ \). Нужно найти значения неизвестной функции \( \pmb \) в узлах сетки \( t_n \). Обозначим через \( \pmb^n \) приближенное значение \( \pmb(t_n) \).

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения \( \pmb^ \) на основе предыдущих вычисленных значений \( \pmb^k \), \( k 0 \) при \( \tau\to 0 \).

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами \( t_n \) и \( t_ \): $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки \( t_n \) это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг \( \tau \), который даст численное приближение \( u^\prime(t_n) \): $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по \( \tau \), т.е. \( O(\tau) \). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение \( y^n \) для того, чтобы решить уравнение (5) относительно \( y^ \) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое \( t_ \): $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение \( \pmb^0 = \pmb_0 \), мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины \( m+1 \) (\( m \) — размерность задачи), а функция F должна возвращать numpy -массив размерности \( m+1 \), t[n] — значение в момент времени \( t_n \).

Таким образом численное решение на отрезке \( [0, T] \) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции \( F \) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое \( t_ \) нужно решить нелинейное уравнение относительно \( \pmb^ \): $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на \( s \) вычислениях функции \( \pmb \) и называется \( s \)-стадийной. Если \( a_ = 0 \) при \( j \geq i \) имеем явный метод Рунге—Кутта. Если \( a_ = 0 \) при \( j > i \) и \( a_ \ne 0 \), то \( \pmb_i \) определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах \( \pmb^n \) и \( \pmb^ \) — один шаг по переменной \( t \). Линейный \( m \)-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов \( a_i \), \( b_i \), \( i = 0, 1, \ldots, m \), причем \( a_0 \ne 0 \). Для начала расчетов по рекуррентной формуле (13) необходимо задать \( m \) начальных значений \( \pmb^0 \), \( \pmb^1 \), \( \dots \), \( \pmb^ \) (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции \( \pmb^ = \pmb(t_, \pmb^) \), \( \pmb^n \), \( \dots \), \( \pmb^ \), т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям \( \pmb^n \), \( \pmb^ \), \( \dots \), \( \pmb^ \) и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке \( u = w \) передаются линейной системой $$ \begin \frac