Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
В этой статье мы поговорим о том, как составляется уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Сначала разберем принцип нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, после чего подробно разберем решения характерных примеров и задач.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана точка 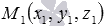
Сначала вспомним один важный факт.
На уроках геометрии в средней школе доказывается теорема: через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к данной прямой (доказательство этой теоремы Вы можете найти в учебнике геометрии за 10 — 11 классы, указанном в списке литературы в конце статьи).
Теперь покажем, как находится уравнение этой единственной плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Мы можем написать общее уравнение плоскости, если нам известны координаты точки, лежащей в этой плоскости, и координаты нормального вектора плоскости.
В условии задачи нам даны координаты x1 , y1 , z1 точки М1 , через которую проходит плоскость 
Любой направляющий вектор прямой a представляет собой нормальный вектор плоскости 
В свою очередь, координаты направляющего вектора прямой a могут определяться различными способами, зависящими от способа задания прямой a в условии задачи. Например, если прямую a в прямоугольной системе координат задают канонические уравнения прямой в пространстве вида 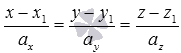
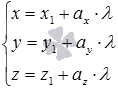
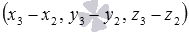
Итак, получаем алгоритм для нахождения уравнения плоскости 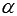
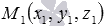
- находим координаты направляющего вектора прямой a (
);
- принимаем координаты направляющего вектора прямой a как соответствующие координаты нормального вектора
плоскости
(
, где
);
- записываем уравнение плоскости, проходящей через точку
и имеющей нормальный вектор
, в виде
— это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Из найденного общего уравнения плоскости вида 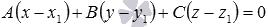
Примеры составления уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Рассмотрим решения нескольких примеров, в которых находится уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
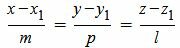 . . | (1) |
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
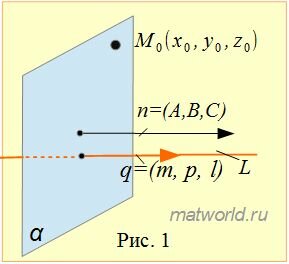 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (3) |
Упростим уравнение (3):
| mx+py+lz+D=0, | (4) |
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
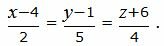 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (8) |
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
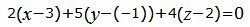 | (9) |
Упростим уравнение (9):
| 2x+5y+4z−9=0. | (10) |
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
 | (11) |
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
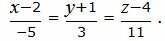 | (11′) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (12) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (13) |
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
 |
Упростим уравнение (13):
| −5x+3y+11z+77=0. | (14) |
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
Уравнение плоскости, проходящей через точку перпендикулярно вектору
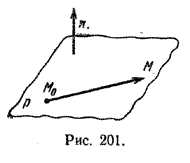
Пусть дана некоторая точка M0 и ненулевой вектор n. Через точку M0 можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).
Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор \(\overrightarrow
Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.
Пусть точка M0 и вектор n заданы своими координатами в некоторой прямоугольной системе координат:
Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор \(\overrightarrow
Это уравнение называется уравнением плоскости, проходящей через точку (х0; у0; z0) перпендикулярно вектору (А; В; С).
Задача 1. Найти уравнение плоскости, проходящей через точку М0(-3; 4; 7) перпендикулярно вектору n = (1; —2; 6).
В данном случае х0 = -3, у0 = 4, z0 = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение
3адачa 2. Даны точки M1 (2; -1; 3) и M2(4; 5; 0). Написать уравнение плоскости, проходящей через точку М2 перпендикулярно вектору \(\overrightarrow
За нормальный вектор плоскости можно взять вектор n = \(\overrightarrow
Задача 3. В треугольнике с вершинами в точках А1<-5; 2; 7), А2(5; 0; 6), А3(0; -1; 2) проведена медиана А1М0. Найти уравнение плоскости, проходящей через точку М0 перпендикулярно медиане А1М0.
За нормальный вектор плоскости можно принять вектор n = \(\overrightarrow
Координаты нормального вектора n = (А; В; С), следовательно, равны
A = 5 /2 + 5 = 15 /2, В = — 1 /2 — 2 = — 5 /2, С = 4 — 7 = — 3.
http://matworld.ru/analytic-geometry/uravnenie-ploskosti3-online.php
http://razdupli.ru/teor/95_uravnenie-ploskosti-prohodyacshej-cherez-tochku-perpendikulyarno-vektoru.php
 );
);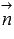 плоскости
плоскости 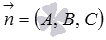 , где
, где 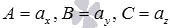 );
);