Как найти амплитуду скорости из уравнения

Как найти амплитуду скорости из уравнения

Гармоническое колебательное движение и волны

Уравнение движения точки дано в виде . Найти период колебаний Т, максимальную скорость v_max и максимальное ускорение a_max точки.

Дано:

Решение:

Уравнение колебаний запишем в виде

Скорость колеблющейся точки

Ускорение колеблющейся точки

Период колебаний Т выразим через циклическую частоту

Уравнение гармонических колебаний

п.1. Гармонические колебания как простейший периодический процесс

Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.

Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10 -14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·10 15 с

Если состояние системы характеризуется некоторой функцией от времени \(s=x(t)\), то для периодического процесса выполняется равенство: \(x(t+T)=x(t)\).
Простейшими периодическими функциями являются тригонометрические функции \(sin⁡t\) и \(cos⁡t\) с периодом \(T=2\pi\).

Множитель \(\omega\) перед аргументом \(t\) тригонометрической функции сокращает её период в \(\omega\) раз (см. §8 данного справочника). Поэтому:

Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при \(t_0=0\), значит, будем описывать колебания по закону косинуса с начальной фазой \(\varphi_0=0\). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: \begin \nu=\frac Nt,\ \ \omega=2\pi\nu=2\pi\frac Nt\\ \omega=2\pi\cdot\frac<20><10>=4\pi\ \text <(рад/с)>\end Получаем закон колебаний: \(x(t)=5cos(4\pi t)\)

п.2. Перемещение, скорость и ускорение при гармоническом движении

Пусть \(x(t)\) — координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acos⁡\omega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-A\omega sin\omega t=A\omega cos⁡\left(\omega t+\frac\pi 2\right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на \(\frac\pi 2\). Амплитудное значение скорости: $$ v_m=A\omega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x»(t)=-A\omega^2 cos\omega t=A\omega^2 cos⁡(\omega t+\pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на \(\frac\pi 2\) и колебания координаты на \(\pi\). Амплитудное значение ускорения: $$ a_m=A\omega^2 $$ Например:
При A=2 и \(\omega=\frac12\) получаем такие синусоиды:

Из уравнения для ускорения получаем: $$ x»(t)=-A\omega^2cos\omega t=-\omega^2(Acos\omega t)=-\omega^2 x(t) $$ Откуда следует:

Решением этого уравнения в общем виде будут: $$ x(t)=Asin⁡(\omega t+\varphi_0)\ \text<или>\ x(t)=A cos⁡(\omega t+\varphi_0) $$ Для каждой из систем физический смысл \(x(t)\) и \(\omega\) будет разным.

п.3. Примеры

Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?

Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения.

По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: \(F=-k\cdot x(t)\)
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: \begin F=ma=m\cdot x»(t)\\ m\cdot x»(t)=-k\cdot x(t) \end Уравнение движения грузика: $$ x»(t)+\frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: \(\omega=\sqrt<\frac km>\)
Общее решение уравнения: \(x(t)=Acos\left(\sqrt<\frac km>+\varphi_0\right)\)
Амплитудные значения скорости и ускорения: $$ v_m=A\sqrt<\frac km>,\ \ a_m=A\frac km $$ Ответ: \(\omega=\sqrt<\frac km>\)

Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?

Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g.

Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?

LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем.

Напряжение на конденсаторе \(U_C(t)=\frac\). Ток, протекающий через катушку, создает ЭДС \(\varepsilon_L(t)=-L\frac<\triangle I><\triangle t>\). При переходе к пределу \(\triangle t\rightarrow 0\) получаем производную \(\varepsilon_L(t)=-LI'(t)\). По второму закону Кирхгофа для замкнутого контура: \begin U_c(t)=\varepsilon_L(t)\Rightarrow \frac=-LI'(t)\Rightarrow \frac+LI'(t)=0 \end Вспомним, что \(Q'(t)=I(t)\) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда \(I'(t)=Q»(t)\).
\begin \frac+LQ»(t)=0 \end Получаем уравнение гармонических колебаний: $$ Q»(t)=\frac<1>Q(t)=0,\ \ \omega=\frac<1><\sqrt> $$ Общее решение уравнения: \(Q(t)=Q_m cos\left(\frac<1><\sqrt>t+\varphi_0\right)\)
Напряжение на конденсаторе: $$ U_C(t)=\frac=\fraccos\left(\frac<1><\sqrt>t+\varphi_0\right) $$ Амплитудное значение напряжения: \(U_m=\frac\)
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-\frac<\sqrt>sin\left(\frac<1><\sqrt>t+\varphi_0\right)=\frac<\sqrt>cos\left(\frac<1><\sqrt>t+\varphi_0+\frac\pi 2\right) $$ Амплитудное значение тока: \(I_m=\frac<\sqrt>\)
Ток опережает колебания заряда и напряжения на \(\frac\pi 2\)

Амплитуда скорости груза

Скорость груза пружинного маятника

Рассмотрим пружинный маятник, который представляет собой груз массой $m$, подвешенный на пружине, которую считают абсолютно упругой (ее коэффициент упругости равен $k$). Пусть груз движется вертикально, движения происходят под воздействием силы упругости пружины и силы тяжести, если система выведена из состояния равновесия и предоставлена самой себе. Массу пружины считаем малой в сравнении с массой груза. Начало отсчета поместим на оси X (ось направлена вниз) в точке равновесия груза.

Пружинный маятник является примером гармонического осциллятора. Колебания гармонического осциллятора служат важным примером периодического движения и являются моделью во многих задачах физики. Колебания такого груза можно считать гармоническими и описывать при помощи уравнения:

где $x\left(t\right)$ — смещение груза от положения равновесия в момент времени ($t$); $<\omega >_0=\sqrt<\frac>>0$- циклическая частота колебаний маятника, $A$- амплитуда колебаний; $<(\omega >_0t+\alpha )$ — фаза колебаний; $\alpha $ — начальная фаза колебаний.

Скорость колебаний груза при этом найдем как:

Амплитудой скорости колебаний груза при этом является величина равная:

Для пружинного маятника амплитуда колебаний скорости груза равна:

Амплитуда скорости колебаний математического и физического маятников

Будем считать математический маятник шариком (грузом), подвешенным на длинной невесомой и нерастяжимой нити. Математический маятник является примером гармонического осциллятора, совершающим колебания, которые описывает уравнение:

Решением уравнения (5) является выражение:

где $\varphi $ — угол отклонения нити от положения равновесия, $\alpha $ — начальная фаза колебаний; $<\varphi >_0$ — амплитуда колебаний; $<\omega >_0=\sqrt<\frac>$ — циклическая частота колебаний.

Амплитудой скорости колебаний груза на нити в данном случае является величина равная:

Для математического маятника амплитуда скорости колебаний груза равна:

Примеры задач на амплитуду скорости груза

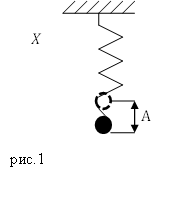
Задание. Колебательная система представляет собой груз, массы $m,\ $подвешенный на упругой пружине (рис.1). Смещение груза вдоль оси X изменяется по закону: $x(t)=2<\cos (10\ t)(м)\ >.$ Чему равно максимальное значение кинетической энергии груза ($E_$)?

Решение. Кинетическую энергию груза можно найти и определения:

Из уравнения колебаний груза найдем уравнение изменения его скорости:

Используя выражение (1.2) получим уравнение изменения кинетической энергии в виде:

Из выражения (1.3) следует, что максимальное значение кинетической энергии (ее амплитуда), учитывая, что $^2\left(10t\right)\le 1$ равно:

Ответ. $E_=200\cdot \ m$ Дж

Задание. Скорость колебаний груза на нити (математический маятник) изменяется в соответствии с гармоническим законом: $\frac