Дифференциальное уравнение Риккати
Общее решение этого уравнения можно получить только в некоторых частных случаях.
Решение дифференциального уравнения Риккати при известном частном решении
Рассмотрим дифференциальное уравнение Риккати:
(1) .
Пусть известно его частное решение :
Тогда подстановкой уравнение Риккати (1) приводится к уравнению Бернулли:
;
;
;
;
.
Это уравнение Бернулли с n = 2 .
Свойства уравнения Риккати
Не меняет вид уравнения:
- Произвольное преобразование независимого переменного:
- Произвольное дробно-линейное преобразование зависимого переменного:
При таких подстановках уравнение также является уравнением Риккати, но с другими функциями p, q, r.
Вид общего решения
Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:
И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.
Упрощение уравнения Риккати
Снова рассмотрим дифференциальное уравнение Риккати:
(1) .
Подстановкой
,
где А – постоянная, оно приводится к виду:
(2) ,
где .
Далее, подстановкой
оно приводится к виду:
(3)
где .
Упрощенное уравнение Риккати
Упрощенное уравнение Риккати – это уравнение вида:
(4) ,
где A, B – постоянные. Оно интегрируется при
,
где – целое.
Покажем это. Сделаем подстановку:
;
.
Подставляем в (4):
.
Умножаем на :
(5) .
Но
.
Подставляем в (5):
Или
(6)
где
.
Уравнение (6) интегрируется при
.
Для этого разделим его на и перепишем в следующем виде:
;
;
.
Это уравнение с разделяющимися переменными. Оно легко интегрируется.
При уравнение (6) можно преобразовать двумя путями.
- Подстановкой , где , оно преобразуется к виду: .
- Подстановкой , где , оно преобразуется к виду:
Таким образом, при , где n — целое число, ряд подстановок приводит к полному решению.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 14-08-2012
Дифференциальное уравнение Риккати
Дифференциальное уравнение первого порядка вида
где — известные функции, называется уравнением Риккати (обобщенным). Если коэффициенты в уравнении Риккати постоянны, то уравнение допускает разделение переменных, и мы сразу получаем общий интеграл
Как показал Лиувилль, уравнение (1) в общем случае не интегрируется в квадратурах.
Свойства уравнения Риккати
1. Если известно какое-нибудь частное решение уравнения (1), то его общее решение может быть получено при помощи квадратур.
В самом деле, положим
где — новая неизвестная функция. Подставляя (2) в (1), найдем
откуда, в силу того что есть решение уравнения (1) получим
Уравнение (3) является частным случаем уравнения Бернулли.
Пример 1. Решить уравнение Риккати
зная его частное решение .
Решение. Положим и подставим в уравнение (4); получим
Таким образом, общее решение уравнения (4) .
Замечание. Вместо подстановки (2) часто бывает практически более выгодной подстановка
которая сразу приводит уравнение Риккати (1) к линейному .
2. Если известны два частных решения уравнения (1), то его общий интеграл находится одной квадратурой.
Пусть известны два частных решения и уравнения (1). Используя тот факт, что имеет место тождество
представим уравнение (1) в виде
Для второго частного решения аналогично находим
Вычитая из равенства (5) равенство (6), получаем
Пример 2. Уравнение имеет частные решения . Найти его общий интеграл.
Решение. Используя формулу (7), получаем общий интеграл исходного уравнения
Решение дифференциального уравнения Риккати при известном частном решении
Пусть известно частное решение y1(x) уравнения Риккати:
Тогда подстановкой y = y1 + u такое уравнение приводится к уравнению Бернулли:
Это уравнение Бернулли с n = 2.
Свойства уравнения Риккати
Не меняет вид уравнения:
Произвольное преобразование независимого переменного:
Произвольное дробно-линейное преобразование зависимого переменного:
При таких подстановках уравнение также является уравнением Риккати, но с другими функциямиp, q, r.
Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:
И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.
Упрощение уравнение Риккати
где А — постоянная, уравнение Риккати приводится к виду:
оно приводится к виду:
Упрощенное уравнение Риккати
Упрощенное уравнение Риккати — это уравнение вида:
 | (1) |
где A, B — постоянные. Оно интегрируется при
где n = ±1, ±2, ±3,… — целое. Сделаем подстановку:
Подставляем в (1):
Умножаем на x 2 :
 | (2) |
Подставляем в (2):
 | (3) |
Уравнение (3) интегрируется при 
Это уравнение с разделяющимися переменными. Оно легко интегрируется.
При 
- Подстановкой
, где
, оно преобразуется к виду:
- Подстановкой
, где
, оно преобразуется к виду:
Таким образом, при 
Уравнения в полных дифференциалах.
Дифференциальные уравнения первого порядка в полных дифференциалах – это уравнения вида
Если выполняется условие:
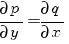 | (1) |
является дифференциалом некоторой функции:
 | (2) |
 | (3) |
Отсюда получаем его интеграл:
Как распознать дифференциальное уравнение в полных дифференциалах
Для того чтобы определить, что уравнение является уравнением в полных дифференциалах, нужно проверить выполнение соотношения (1). Поскольку вычисление производной занимает некоторое время, то сначала желательно проверить, не принадлежит ли уравнение одному из рассмотренному выше типов.
Методы решения дифференциальных уравнений в полных дифференциалах
Метод последовательного выделения дифференциала
Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
v du + u dv = d(uv)
В этих формулах u и v — произвольные выражения, составленные из любых комбинаций переменных.
Метод последовательного интегрирования
Проинтегрируем первое уравнение (2):
где φ — функция от y.
Подставляем во второе уравнение (2):
Интегрируя находим φ и, тем самым, U.
http://mathhelpplanet.com/static.php?p=differentsialnoe-uravnenie-rikkati
http://poisk-ru.ru/s22058t14.html
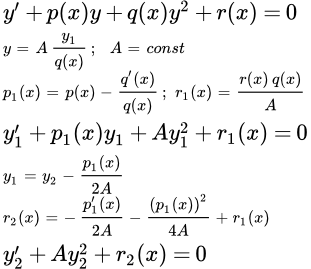


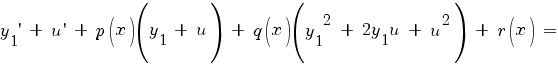





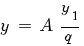







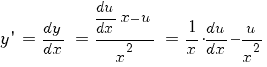



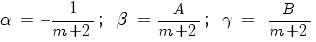



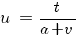 , где
, где  , оно преобразуется к виду:
, оно преобразуется к виду:
 , где
, где  , оно преобразуется к виду:
, оно преобразуется к виду: