Как найти делитель в уравнении с остатком

Конспект урока по математике в 4-м классе «Правило нахождения неизвестного делителя при делении с остатком»

Главная цель урока: познакомить с правилом нахождения неизвестного делителя при делении с остатком.

Образовательные цели:

Воспитательные цели:

Развивающие цели:

Оздоровительные цели:

Оборудование:

Ход урока

1. Организационный момент.

Эмоциональный настрой на урок

— Сегодня у нас много гостей на уроке. Повернитесь, поздоровайтесь и улыбнитесь им. Вот видите, и они вам улыбнулись. В классе стало уютно от ваших улыбок.

На доске написана цифра 9.

— Сегодня на уроке мы с вами будем повторять написание цифры 9.

— Напишите три цифры.

— Оцените свою работу. Если вы считаете, что все три цифры написали каллиграфически верно, поставьте на полях тетради знак плюс, если нет — знак минус.

3. Актуализация знаний.

“Разминка для головы и рук”

— Что движется быстрее скорости света?

— Мне интересно будет сегодня на уроке наблюдать, как движутся ваши мысли. Не прячьте их.

18 : 9 2 27 : 9 3

— Что записано на доске?

— Прочитайте выражения разными способами.

— Найдите закономерность записи чисел и выражений.

— Какое деление выполнили?

— Продолжите закономерность до конца строчки.

— Что общего во всех выражениях?

— Как найти неизвестный делитель?

— Найдите компоненты действия деления.

— Какой компонент неизвестен в первом примере?

На доске представлена таблица. У каждого учащегося на парте карточка с числом, которое является значением одного из выражений. Всем учащимся необходимо выполнить устные вычисления и прикрепить свою карточку в нужное место таблицы. Примеры решаются по порядку, карточки прикрепляются по мере решения примеров.

4. Сообщение темы и задач урока.

— Теперь нам надо узнать тему нашего урока.

На доске открывается схематическое изображение темы урока.

— Какое деление сегодня мы будем выполнять на уроке?

— Какие компоненты при делении с остатком умеем находить?

— Какой компонент будем сегодня учиться находить?

— Задача нашего урока составить формулу нахождения неизвестного делителя при делении с остатком.

5. Этап “открытия” нового знания.

На доске открывается запись.

— Подумайте, как мы будем находить неизвестный делитель?

— Можем ли мы использовать формулу нам уже известную?

— Давайте уберём остаток. Как это сделать?

— Теперь можем воспользоваться уже известной нам формулой?

— Можем ли мы теперь ответить на главный вопрос урока?

— Как найти неизвестный делитель при делении с остатком?

На доске открывается формула нахождения неизвестного делителя при делении с остатком.

— Откройте учебники на стр. 61, найдите №122.

— Используя данную формулу, вставьте числа в “окошки”.

— Считайте устно и комментируйте свой ответ.

6. Физкультурная минутка.

1) И.п.- сидя за партой, руки за голову. 1-2-руки вверх, потянуться; 3-4-И.п.

2) И.п.- сидя за партой, ноги на ширину плеч, руки на пояс. 1-2- наклон вправо; 3-4 – И.п. То же влево.

3) И.п. – сидя за партой. 1-2- встать, выпрямиться; 3-4 – И.п.

7. Закрепление пройденного материала.

— Что мы будем делать дальше на уроке, ведь на главный вопрос урока мы дали ответ?

— Зачем нам тренироваться в решении примеров на нахождение неизвестного делителя?

Учащиеся получают карточки для самостоятельной работы.

— Найдите неизвестный делитель. Закройте окошки.

— Выполненную работу передайте члену своей пары. Оцените работы.

— При выполнениеиработы без ошибок, передайте члену пары карточку со знаком плюс. При ошибках в вычислениях передайте карточку со знаком минус.

На доске открываются значения выражений, представленные на карточках.

— А теперь сравните свои результаты с результатами на доске.

— Если результаты совпали, оставьте карточку со знаком плюс, если нет, верните ее обратно члену пары, который проверял вашу работу.

— Откройте учебник на стр.64.

— Прочитайте задачу № 28.

— Как вы думаете, почему именно данная задача включена в урок?

— Что в задаче известно?

— Что значит “по 6 банок тушёнки”?

— Что надо узнать?

— Можем сразу ответить на вопрос задачи?

— Теперь можем ответить на поставленный вопрос?

— Что для этого нужно сделать?

— А как письменно оформить нашу мысль?

— Что мы записали?

— Прочитайте, как рассуждали при решении данной задачи Миша и Маша.

— С чьим рассуждением совпадает наше?

— Кто прав: Маша и мы или Миша?

9. Подведение итогов урока. Домашнее задание. Инструктаж его выполнения.

— Оцените себя и покажите, кто может самостоятельно в домашнем задании найти делитель при делении с остатком?

Учащиеся показывают карточки с условными знаками: +,-, ?.

— Кому необходимо пользоваться формулой при решении примеров на нахождение неизвестного делителя при делении с остатком?

Учащиеся показывают карточки с условными знаками: +,-, ?.

— В домашнем задании я предлагаю вам составить примеры на деление с остатком с неизвестным делителем. Напечатайте примеры, используя компьютер. У вас получатся карточки для самостоятельной работы. Мы будем использовать их на следующих уроках.

-Урок окончен. Ваши мысли двигались действительно быстрее скорости света. Мне было интересно и комфортно на уроке.

— А как вы ощущали себя на уроке?

Каждый учащийся работает с индивидуальными текстовыми карточками

— Выберите утверждение. Отметьте галочкой.

Ощущал себя на уроке:

• хорошо;
• уверенно;
• смело;
• гордо;
• комфортно;
• глупо;
• неуверенно;
• испуганно;
• сердито;
• грустно.

Деление натуральных чисел с остатком: правило, примеры решений

Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.

Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.

Деление натуральных чисел столбиком с остатком

Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.

Приведем решение примера, так как понять суть метода проще всего на практике.

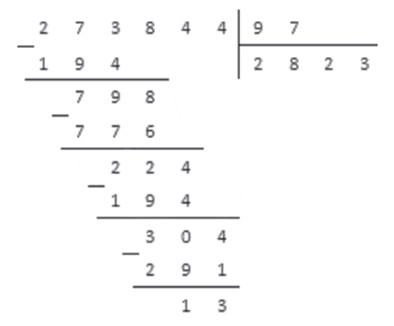
Пример 1. Как делить натуральные числа с остатком?

Разделим натуральное число 273844 на натуральное число 97 .

Проводим деление столбиком и записываем:

Результат: неполное частное от деления равно 2823 , а остаток равен 13 .

Деление чисел с остатком через последовательное вычитание

Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.

Пример 2. Деление с остатком через последовательное вычитание.

Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .

Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 — 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 — 3 = 1 яблоко.

1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:

7 ÷ 3 = 2 (остаток 1)

Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3 .

Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.

Пример 3. Деление с остатком через последовательное вычитание.

Вычислим: 145 ÷ 46 .

Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:

Повторяем эту операцию еще раз:

В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .

145 ÷ 46 = 3 (остаток 7) .

Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.

Если a b , то a ÷ b = 0 (остаток a) .

12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)

Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.

Метод подбора неполного частного

При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.

Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.д.

Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a — b · c . Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.

В-третьих, не будем забывать, что остаток всегда меньше делителя.

Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т.д. Применяя формулу d = a — b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.

Разберем применение этого метода на примере.

Пример 4. Деление с остатком методом подбора

Разделим 267 на 21 .

a = 267 ; b = 21 . Подберем неполное частное.

Используем формулу d = a — b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.

Если с = 0 , имеем: d = a — b · c = 267 — 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.

При с = 1 имеем: d = a — b · c = 267 — 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.

При с = 2 имеем: d = a — b · c = 267 — 21 · 2 = 267 — 42 = 225 ; 225 > 21 .

При с = 3 имеем: d = a — b · c = 267 — 21 · 3 = 267 — 63 = 204 ; 204 > 21 .

При с = 12 имеем: d = a — b · c = 267 — 21 · 12 = 267 — 252 = 15 ; 15 21 .

На этом этапе процесс деления можно считать законченным. Неполное частное с = 12 , а остаток деления равен 15 .

Алгоритм деления натуральных чисел с остатком

Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.

Вспомним, что в случае, когда a b, неполное частное равно нулю, а остаток равен делимомому a . Мы будем рассматривать случай, когда a > b .

Сформулируем три вопроса и ответим на них:

1. Что там известно?
2. Что нам нужно найти?
3. Как мы будем это делать?

Изначально известными являются делимое и делитель: a и b .

Найти нужно неполное частное c и остаток d .

Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.

Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .

1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.

Запомним это число.

2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.

В нашем примере справа от 47 дописываем нуль. Так как 470 899 , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.

3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.

4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.

Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .

470 899 , поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47 · 20 = 940 ; 940 > 899 .

Число, которое мы получили на предпоследнем шаге ( 470 = 47 · 10 ) является первым из искомых слагаемых.

5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.

Шаги 1 — 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 — 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.

Обратимся к примеру. 899 — 470 = 429 , 429 > 47 . Повторяем шаги 1 — 5 алгоритма с числом 429 , взятым в качестве делимого.

1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу — число 1 .

2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 — 1 = 0 . Запоминаем 0 .

3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы

4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 429 , 47 · 10 = 470 > 429 . Таким образом, второе искомое слагаемое — 47 · 9 = 423 .

5. Разность между 429 и 423 равна числу 6 . Так как 6 47 , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.

6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:

899 = 47 · 10 + 47 · 9 + 6

Применим распределительное свойство умножения.

899 = 47 · 10 + 47 · 9 + 6 = 47 · ( 10 + 9 ) + 6

Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .

Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .

Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:

Пример 5. Деление натуральных чисел с остатком

Разделим числа 42252 и 68 .

Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800 = 68 · 600 .

Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 — 40800 и получаем второе слагаемое 1360 = 68 · 20

Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 — 1360 . Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 — 68 .

В результате получаем:

42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · ( 600 + 20 + 1 ) + 24 = 68 · 621 + 24

Неполное частное равно 621 , остаток равен 24 .

Деление натуральных чисел с остатком. Проверка результата

Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.

На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.

Остаток всегда меньше делителя!

На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.

Пример 6. Проверка результата деления натуральных чисел с остатком.

Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .

Сравниваем остаток и делитель: 30 > 28 .

Значит, деление выполнено неверно.

Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?

Чтобы узнать это, сначала сравниваем остаток и делитель: 5 13 .

Первый пункт проверки пройден, переходим ко второму.

Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .

Подставляем значения и сравниваем результаты

13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122

Значит, в вычисления школьника где-то закралась ошибка.

Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 . Все ли правильно посчитано?

Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.

Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .

После подстановки, имеем:

5998 = 111 · 54 + 4 = 5994 + 4 = 5998 .

Равенство корректно, а значит, и деление выполнено верно.

Деление чисел с остатком

О чем эта статья:

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Теорема

a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя
• получить неполное частное и остаток;
• записать число противоположное полученному.

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Проверка : a = b * q + r, 17 = −5 * (−3) + 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:

r = a − b * q

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

• найти модули делимого и делителя;
• разделить по модулю;
• записать противоположное данному число и вычесть 1;
• использовать формулу для остатка r = a − b * q.

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:

r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Проверка: a = b * q + r, −17 = 5 * (−4) + 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

r = a − b * q

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя;
• получить неполное частное и остаток;
• прибавить 1 к неполному частному;
• вычислить остаток, исходя из формулы r = a − b * q.

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Проверка: a = b * q + r, −17 = −5 * 4 + 3.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.