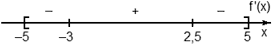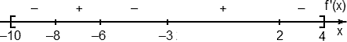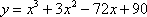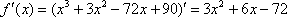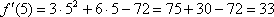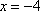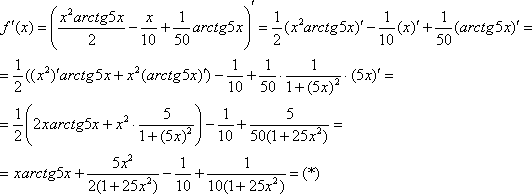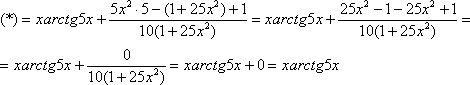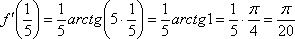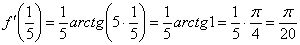Как найти производную функции в точке x0
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
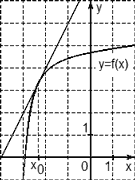
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
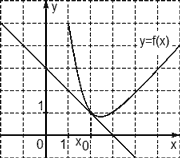
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
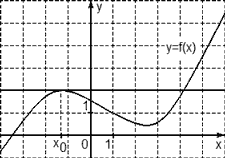
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
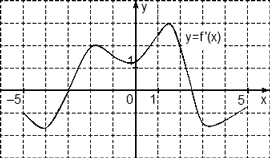
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
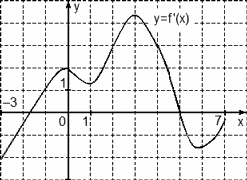
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
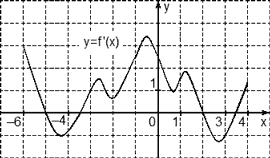
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
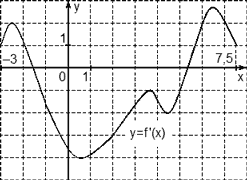
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
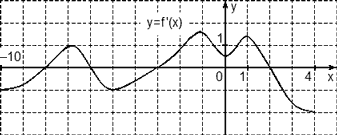
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции 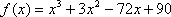
Справка: Следующие способы обозначения функции эквивалентны: 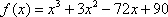
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке 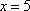
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции 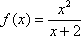
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции 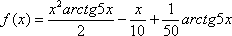
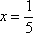
Производная, в принципе, найдена, и можно подставлять требуемое значение 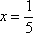
Ну вот, совсем другое дело. Вычислим значение производной в точке 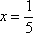
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции 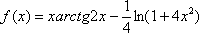
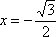
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной кграфику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции 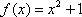
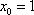
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственнойточке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при 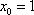
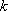
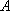
И наша задача состоит в том, чтобы найти уравнение прямой 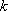
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции 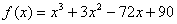
Справка: Следующие способы обозначения функции эквивалентны:
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке 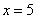
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции 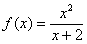
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции 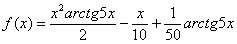
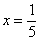
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение 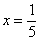
Ну вот, совсем другое дело. Вычислим значение производной в точке 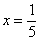
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции 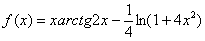
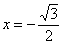
Это пример для самостоятельного решения.
Как найти значение производной функции F(x) в точке Хо? Как вообще это решать?
Sfash
Если формула задана, то найти производную и вместо Х подставить Х-нулевое. Посчитать
Если речь идет о б-8 ЕГЭ, график, то надо найти тангенс угла (острый или тупой) , который образует касательная с осью Х (с помощью мысленного построения прямоугольного треугольника и определения тангенса угла)
Тимур адильходжаев
Во-первых, надо определиться со знаком. Если точка х0 находится в нижней части координатной плоскости, то знак в ответе будет минус, а если выше, то +.
Во-вторых, надо знать что такое тангес в прямоугольном прямоугольнике. А это соотношение противолежащей стороны (катета) к прилежащей стороне (тоже катета) . На картине обычно есть несколько черных отметок. Из эти отметок составляешь прямоугольный треугольник и находишь тангес.
Как найти значение производной функции f x в точке x0?
Bk.Ru
В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, т.е. в Вашем случае подставить нулевой Х и вычислить полученное выражение.
Ну а ваше стремление разобраться в этом вопросе, на мой взгляд, бесспорно заслуживает +, который ставлю с чистой совестью.
Lady v
Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной (не саму производную заметьте!) в указанной точке Х0. Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. Потом составляется уравнение этой касательной в виде y=кx+b.
В этом уравнении коэффициент к и будет являться значением производной. остается лишь найти значение коэффициента b. Для этого находим значение у при х=о, пусть оно равно 3 — это и есть значение коэффициента b. Подставляем в исходное уравнение значения Х0 и У0 и находим к — нашу значение производной в этой точке.
Применение производной для решения нелинейных уравнений и неравенств
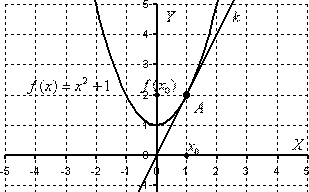
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. \begin
Если две точки экстремума найдены, но \(f(x_1)\cdot f(x_2)=0\), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
| 1) \(x^3+3x^2-4=0\) \(b^2-3ac=9\gt 0 (c=0) \) \(f(x)=x^3+3x^2-4 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-4,\ f(x_2)=0 \) \(f(x_1)\cdot f(x_2)=0\Rightarrow\) два корня  | 2) \(x^3+3x^2-1=0\) \(b^2-3ac=9\gt 0 \) \(f(x)=x^3+3x^2-1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-1,\ f(x_2)=3 \) \(f(x_1)\cdot f(x_2)\lt 0\Rightarrow\) три корня  |
| 3) \(x^3+3x^2+1=0\) \(b^2-3ac=9\gt 0\) \(f(x)=x^3+3x^2+1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=1,\ f(x_2)=5 \) \(f(x_1)\cdot f(x_2)\gt 0\Rightarrow\) один корень  | 4) \(x^3+x^2+x+3=0\) \(b^2-3ac=1-3\lt 0 \) Один корень  |
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения \(\frac 1x+\frac<1>
б) Найдите число корней уравнения \(\frac 1x+\frac<1>
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью \(y=1\). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=\frac1x+\frac<1>
1) ОДЗ: \(x\ne\left\<0;1;3\right\>\)
Все три точки – точки разрыва 2-го рода. \begin
Функция непериодическая.
3) Асимптоты
1. Вертикальные \(x=0, x=1, x=3\) – точки разрыва 2-го рода
2. Горизонтальные: \begin
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: \(k=0\), нет.
4) Первая производная $$ f'(x)=-\frac<1>
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. \(x=0\) – асимптота
Точки пересечения с OX – две, \(0\lt x_1\lt 1,1\lt x_2\lt 3\)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь \(y=k\) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При \(k\lt 0\) — три корня
При \(k=0\) — два корня
При \(k\gt 0\) — три корня
Ответ: а) 3 корня; б) при \(k=0\) два корня, при \(k\ne 0\) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ \sqrt
Исследуем функцию \(f(x)=\sqrt
ОДЗ: \( \begin
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: \(f(1)=0+\sqrt<8>=2\sqrt<2>,\ f(5)=\sqrt<4>+0=2\)
Первая производная: \begin
| \(x\) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| \(f'(x)\) | ∅ | + | 0 | — | ∅ |
| \(f(x)\) | \(2\sqrt<2>\) | \(\nearrow \) | max \(2\sqrt<3>\) | \(\searrow \) | 2 |
Можем строить график:
\(y=a\) — горизонтальная прямая.
Количество точек пересечения \(f(x)\) и \(y\) равно количеству решений.
Получаем:
| $$ a\lt 2 $$ | нет решений |
| $$ 2\leq a\lt 2\sqrt <2>$$ | 1 решение |
| $$ 2\sqrt<2>\leq a\lt 2\sqrt <3>$$ | 2 решения |
| $$ a=2\sqrt <3>$$ | 1 решение |
| $$ a\gt 2\sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале \(2\leq a\leq 2\sqrt<3>\).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство \(\frac<2+\log_3 x>
Разобьем неравенство на совокупность двух систем.
Если \(x\gt 1\), то \(x-1\gt 0\), на него можно умножить слева и справа и не менять знак.
Если \(x\lt 1\), то \(x-1\lt 0\), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: \(x\gt 0\)
Получаем совокупность: \begin
Точка разрыва: \(x=\frac12\) – вертикальная асимптота
Односторонние пределы: \begin
Первая производная: $$ f'(x)=\left(1-\frac<3><2x-1>\right)’=\frac<3><(2x-1)^2>\gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-\frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка \(x=\frac12\)
Алгебра
План урока:
Производные некоторых элементарных функций
Ранее мы для вычисления производных использовали ее определение. То есть каждый раз мы давали функции некоторое приращение ∆х, потом находили соответствующую ему величину ∆у, далее составляли отношение ∆у/∆х, после чего находили предел этого отношения при ∆х →0. Выполнение такого алгоритма довольно трудоемко. Поэтому на практике используются специальные формулы для вычисления производных.
Нам известно несколько основных функций, которые в математике чаще называют элементарными. Например, элементарными являются линейная функция, степенная, показательная, логарифмическая. Также существует несколько различных тригонометрических функций (синус, косинус, тангенс), которые тоже считаются элементарными. Попытаемся вычислить для них производные.
Начнем с линейной функции. В общем случае она выглядит так:
где k и b – некоторые постоянные числа.
Выберем произвольную точку х0 и дадим ей приращение ∆х, в результате чего мы придем в новую точку (х0 + ∆х). Вычислим значения линейной функции в этих двух точках:
Теперь мы можем найти приращение функции ∆у:
Находим отношение ∆у/∆х:
Получилось, что это отношение не зависит ни от приращения ∆х, ни от выбора исходной точки х0. Естественно, что предел этого отношения при ∆х→0 (то есть производная) также будет равен k:
Задание. Вычислите производную функции у = 4х + 9.
Обратите внимание, что в рассмотренном примере запись у′ = 4 означает функцию. Просто при любом значении х она принимает одно и то же значение, равное 4. График производной функции будет выглядеть так:
Рассмотрим два особых частных случая линейной функции. Пусть k = 1 и b = 0, тогда она примет вид у = х. Её производная тогда будет равна 1:
Теперь предположим, что коэффициент k = 0. Тогда функция примет вид
где С – некоторое постоянное число, то есть константа (большая буква Св таких случаях используется из-за латинского термина constanta). Производная такой функции будет равна нулю:
Задание. Найдите вторую производную функции у = 9х + 2.
Решение. Сначала вычислим первую производную:
Очень легко объяснить, почему производная константы равна нулю. Представим себе, что закон движения некоторого тела выглядит как s(t) = C, например, s(t) = 5. Это значит, что тело в любой момент времени находится в точке, находящейся в 5 метрах от какого-то начала отсчета. То есть тело находится в одной и той же точке, а это значит, что оно не двигается. Тогда его скорость равна нулю. Но производная – это и есть скорость, значит, она также равна нулю.
Далее вычислим производную для функции у = 1/х. Выберем некоторую точку х0 и дадим ей приращение ∆х. В результате имеем две точки с координатами х0 и (х0 + ∆х). Вычислим значение функции в каждой из них:
Осталось найти предел данного отношения при ∆х→0. Ясно, что при этом множитель х0 + ∆х будет стремится к х0, то есть
Задание. Вычислите производные функции
Обратите внимание, что производная функции у = 1/х оказывается отрицательной при любом значении х (кроме нуля, для которого производную посчитать нельзя, так как получится деление на ноль). Это должно означать, что функция убывает в каждой своей точке, а любая касательная к ней образует с осью Ох тупой угол наклона. И это действительно так:
Мы разобрали несколько простейших примеров того, как находить формулы производных. Для этого используется понятие предела функции. Для вывода всех подобных формул требуется хорошо знать тему вычисления пределов, которая не изучается детально в школе. Поэтому мы просто дадим следующие формулы без доказательств.
Начнем со степенной функции у = х n , где n– некоторое постоянное число. Её производная вычисляется по формуле:
Приведем примеры использования этой формулы:
Задание. Найдите производную функции у = х 6 в точке х0 = 10.
Задание. Движение самолета при разгоне описывается законом движения s(t) = t 3 . Найдите его скорость через 5 секунд после начала разгона.
Решение. Скорость самолета в любой момент времени равна производнойs′(t). Найдем её:
Заметим, что используемая нами формула работает и в том случае, если показатель степени является отрицательным или дробным числом. Действительно, ранее мы вывели формулу
Задание. Вычислите производную функции
Задание. Определите, в какой точке необходимо провести касательную к графику функции
чтобы она образовывала с осью Ох угол в 45°?
Решение. Тангенс угла наклона касательной равен производной. Известно, что tg 45° = 1. Значит, нам надо найти такую точку х0, в которой значение производной квадратного корня будет равно единице. Производная вычисляется по формуле:
Далее изучим формулы производных для тригонометрических функций. Они выглядят так:
Рассмотрим несколько примеров использования этих формул.
Задание. Найдите производную функции у = cosx в точке х0 = π.
Решение. Мы знаем, что
Задание. Найдите угол наклона касательной, проведенной к графику у = sinx в начале координат.
Решение. Производная синуса вычисляется по формуле:
Получается, что тангенс угла наклона также равен единице. Это значит, что сам угол равен 45°. Построение показывает, что это действительно так:
Задание. Найдите производную функции у = tgx в точке х0 = π/6.
Решение. Для тангенса используется формула:
Далее рассмотрим показательную и логарифмическую функцию. Их производные рассчитываются по следующим формулам:
Обратите внимание, что в этих формулах появился натуральный логарифм, то есть логарифм, основанием которого является число е. Именно из-за наличия натурального логарифма в формулах дифференцирования он играет особо важную роль в математике и имеет отдельное обозначение. Вычислим несколько производных с помощью приведенных формул:
Напомним, что справедлива формула
Стоит обратить внимание, что функции у = е х при дифференцировании не меняется. Эта особенность функции также имеет огромное значение в математическом анализе.
Задание. Найдите угол наклона касательных, проведенных к графику у = е х в точке (0; 1) и к графику у = lnx в точке (1; 0).
Решение. Используем формулы производных:
Получили, что тангенс наклона касательной равен 1. Из этого следует, что угол наклона касательной равен 45°. Далее найдем производную натурального логарифма при х = 1:
Производная снова равна 1, значит, угол наклона также составит 45°, что подтверждается рисунком:
Задание. Вычислите производную функции у = 2 х при х0 = 3.
Решение. Используем формулу
Сведем использованные нами равенства в одну таблицу производных основных функций:
Основные правила дифференцирования
До этого мы рассматривали довольно простые, то есть стандартные функции, для каждой из которых производную можно узнать из справочника или таблицы. Но что делать, если нам потребовалось продифференцировать функцию, которая состоит из нескольких основных? Например, что делать с функциями у = 5х 2 + 6х – 3 или у = x•sinx?
Все более сложные функции можно получить из нескольких простых, комбинируя их. Так, функция у = х 3 + х 2 получается сложением функций у = х 3 и у = х 2 , а функция у = (lnx)•(cosx) – произведением функций у = lnx и у = сosx.
Есть несколько правил, которые позволяют находить производные в таких случаях. Мы не будем их доказывать, а просто дадим их формулировки. Также будем нумеровать правила. Первое из них помогает находить производную сумму функций.
В данном случае u и v – это просто обозначение каких-то произвольных функций. Рассмотрим пример. Пусть надо найти производную функции
Правило работает и в том случае, если сумма представляет собой сумму не двух, а большего числа слагаемых:
Следующее правило позволяет выносить постоянный множитель за знак производной:
Покажем использование этого правила:
Действительно, зная эти формулы и первые два правила вычисления производных, мы можем записать, что
Задание. Вычислите значение производной функции у = 9х 3 + 7х 2 – 25х + 7 в точке х0 = 1.
Решение. Пользуясь правилами дифференцирования, находим производную:
Несколько сложнее обстоит дело с дифференцированием функций, получающихся при перемножении простых функций. В таких случаях используется следующее правило:
Предположим, надо найти производную для функции у = х 2 •sinx. Её можно представить как произведение u•v, где
Примечание. В последнем случае мы в конце примера использовали формулу косинуса двойного угла:
Заметим, что иногда одно и то же задание с производной можно решить по-разному, используя или не используя правило для вычисления производной произведения функций.
Задание. Найдите производную функции у = х 2 •(3х + х 3 ). Вычислите ее значение при х = 1.
Решение. Функция у представляет собой произведение более простых функций u•v, где
Задание. Продифференцируйте функцию
Решение. Здесь перед нами функция, которая представляет собой произведение сразу трех множителей. Что делать в таком случае? Надо всего лишь добавить скобки и их помощью оставить только два множителя (один их них окажется «сложным»):
Довольно сложно выглядит формула для поиска производной дроби:
Например, пусть надо найти производную функции
С помощью данного правила можно доказать некоторые равенства. Так, ранее мы уже записали (без доказательства) формулы производных тригонометрических функций:
Оказывается, формула для тангенса может быть выведена из формул для синуса и косинуса. Действительно, тангенс можно записать в виде дроби:
Задание. Найдите, в каких точках надо провести касательную к графику дробно-линейной функции
чтобы эта касательная образовала с осью Ох угол в 135°.
Решение. Угол будет равен 135° только тогда, когда значение производной будет равно (– 1) (так как tg 135° = – 1). Поэтому сначала найдем производную. В данном случае следует использовать правило 4, так как функция у явно записана как дробь:
Получили два значения х. Построив график и проведя касательные, мы убедимся, что они действительно образуют с осью Ох угол 135°:
Заметим, что иногда можно избавиться от необходимости использовать правило 4, если дифференцируемую функцию можно преобразовать. При этом часто помогает использование отрицательных степеней. Пусть надо продифференцировать функцию
Напрашивается решение использовать правило 4.И такой путь позволит получить правильное решение, хотя и будет несколько трудоемким. Однако можно преобразовать функцию:
У нас получилось произведение, а потому можно использовать правило 3, которое представляется более простым:
Производная сложной функции
«Сконструировать» громоздкую функцию из нескольких простых можно не только с помощью арифметических действий. Например, возьмем функции
В обоих случаях мы получили некоторую функцию, продифференцировать которую с помощью уже известных нам правил не получится. Функции, сконструированные таким образом, называются сложными. Есть универсальная формула, позволяющая находить производную сложной функции:
Посмотрим, как пользоваться эти правилом. Пусть надо вычислить производную функции
Она сконструирована из функции у = e x и у = sinx, причем вторая подставлена в первую. Это значит, что первую можно обозначить буквой u, а вторую – буквой v (если использовать обозначения в правиле 5):
Задание. Найдите у′, если у = sin 2x.
Решение. На этот раз в качестве исходной функции выступает
Убедиться в справедливости правила 5 можно на примере функции
Её можно продифференцировать двумя разными способами. Сначала попробуем просто избавиться от квадрата в исходной функции, используя формулу квадрата суммы:
В результате оба способа вычисления производной дали одинаковый ответ.
Задание. Найдите производную сложной функции у = (2х + 5) 1000 .
Решение. В данном случае мы рассматриваем комбинацию следующих функций:
Теперь мы умеем вычислять производные почти любых функций, которые можно записать с помощью элементарных функций и арифметических операций. При этом нам не надо использовать определение понятия производной и вычислять какие бы то ни было пределы. Достаточно знать производные основных функций и несколько (всего лишь 5) правил дифференцирования. Навыки дифференцирования функций пригодятся в будущем при решении практических задач, связанных с производными.
http://reshator.com/sprav/algebra/10-11-klass/primenenie-proizvodnoj-dlya-resheniya-nelinejnyh-uravnenij-i-neravenstv/
http://100urokov.ru/predmety/urok-3-vychislenie-proizvodnoj