Как найти координаты вектора из уравнения

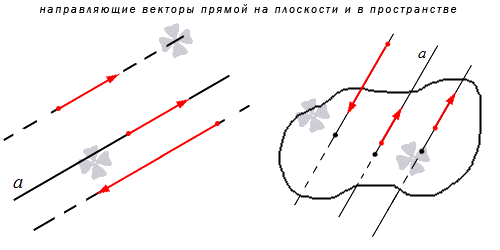Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.

Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .

Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.

Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .

Как вычислить координаты направляющего вектора по уравнениям прямой

Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.

1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.

Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .

Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.

Приведем пример задачи.

В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.

Решение

Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.

Ответ: 4 , — 3 .

Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.

У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.

Решение

Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.

Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0

Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .

А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.

У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.

Решение

В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.

Ответ: ( 0 , 1 )

А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.

1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.

2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.

3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .

Самым простым является первый подход. Проиллюстрируем его на примере задачи.

Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.

Решение

Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:

3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10

Получившееся равенство преобразовываем и получаем:

3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3

Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3

К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.

Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.

Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:

1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z

2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z

Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.

Рассмотрим конкретную задачу.

Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.

Решение

В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.

Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0

Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .

Решение

Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .

Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.

Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?

Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.

Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.

Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.

Решим задачу, в которой применяется этот подход.

Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .

Решение

Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .

У нас получится:

n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →

Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.

Ответ: — 20 , 10 , 0

В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.

2.2.3. Как найти направляющий вектор
по общему уравнению прямой?

Если прямая задана общим уравнением , то вектор является направляющим вектором данной прямой.

Примеры нахождения направляющих векторов прямых:

Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить: так, уравнение задаёт прямую, которая параллельна оси и координаты полученного направляющего вектора удобно разделить на –2, получая в точности базисный вектор в качестве направляющего вектора. Аналогично, уравнение задаёт прямую, параллельную оси , и, разделив координаты вектора на 5, получаем направляющий вектор .

Читателям с низким уровнем подготовки рекомендую постоянно выполнять чертежи, чтобы лучше понимать мои объяснения!

Теперь выполним проверку Задачи 61. Решение уехало вверх, поэтому напоминаю, что в ней мы составили уравнение прямой по точке и направляющему вектору . Проверка состоит в двух действиях:

Во-первых, по уравнению прямой восстанавливаем её направляющий вектор: – всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это несложно заметить по пропорциональности соответствующих координат).

Во-вторых, координаты точки должны удовлетворять уравнению . Подставляем их в уравнение:

– получено верное равенство, чему мы очень рады.

Вывод: задание выполнено правильно.

Задача 62

Составить уравнение прямой по точке и направляющему вектору

Это задача для самостоятельного решения. И проверка, проверка, проверка!

Старайтесь всегда (если это возможно) выполнять проверку на черновике.
Глупо допускать ошибки там, где их 100%-но можно избежать!

В том случае, если одна из координат направляющего вектора равна нулю, поступают очень просто:

Задача 63

Составить уравнение прямой по точке и направляющему вектору .

Решение: формула не годится, так как знаменатель правой части равен нулю. Но выход прост! Используя свойства пропорции, перепишем уравнение в виде , и дальнейшее покатилось по глубокой колее:

переставим части местами:

Ответ:

Проверка:

1) Восстановим направляющий вектор найденной прямой :
– полученный вектор коллинеарен исходному направляющему вектору .

2) Подставим координаты точки в уравнение :

– получено верное равенство, значит, точка удовлетворяет уравнению.

Вывод: задание выполнено правильно

Возникает вопрос: зачем маяться с формулой , если существует универсальная версия , которая сработает в любом случае?

Причин две. Во-первых, формула в виде дроби гораздо лучше запоминается. А во-вторых, недостаток универсальной формулы состоит в том, что здесь повышается риск запутаться при подстановке координат.

Задача 64

Составить уравнение прямой по точке и направляющему вектору , выполнить проверку.

Это задача для самостоятельного решения. Кстати, проверку можно выполнять и графически – решили задачу и изобразили всё на чертеже. Правда, такой способ бывает неудобен или трудновыполнИм, и поэтому всё-таки «рулит» аналитика.