Как найти корень трансцендентного уравнения

Лекция «Приближенные решения алгебраических и трансцендентных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

БИК Курс лекций по дисциплине «Численные методы»

для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем

Раздел 2. Численные методы

2.1.1. Приближенные решения алгебраических и трансцендентных уравнений

Алгебраические и трансцендентные уравнения

Графический метод решения уравнений

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

( x )= g ( x ), (1)

где (х) и g (х) — данные функции, определенные на некотором числовом множестве X , называемом областью допустимых значений уравнения .

В общем случае нелинейное уравнение можно записать в виде:

F ( x ) определена и непрерывна на конечном или бесконечном интервале .

 Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.

 Всякое число , обращающее функцию F ( x ) в нуль, т.е. такое, при котором F ( )=0, называется корнем уравнения (1).

 Число называется корнем k -той кратности, если при x =вместе с функцией F ( x ) равны нулю ее производные до ( k -1) порядка включительно:

F ( ) = F / () = … = F ( k -1) ( ) = 0.

Однократный корень называется простым.

 Решить уравнение – значит найти множество всех корней этого уравнения.

Оно может быть конечным или бесконечным.

 Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .

Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

где a ₀, a ₁, . , a _n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.

Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).

Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.

Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.

При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.

 Решить уравнение – это значит

установить, имеет ли оно корни,

и найти значение корней с заданной точностью.

 Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:

отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,

и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.

Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).

2. Графические методы решения уравнений

Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Рисунок 1

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).

После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀, ординаты обоих графиков в этой точке равны между собой, т. е. f (х₀) = g (х₀). Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

Рисунок 2

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.

Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)

Рисунок 3 Рисунок 4

Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).

Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.

Перепишем уравнение следующим образом: lg х = Зх — 5.

Функции в левой и в правой части уравнения имеют общую область определения: интервал 0

Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x ₁ 0,00001 и x ₂ 1,75. На рисунке трудно показать пересечение графиков этих двух функций в первой точке, однако, учитывая, что нижняя ветвь, логарифмической кривой неограниченно приближается к оси Оу, можно предполагать, что пересечение этих двух графиков произойдет вблизи точки пересечения графика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно равна 0,00001. Итак, корни уравнения x ₁ 0,00001 и x ₂ 1,75

Рисунок 5 Рисунок 6

Пример 3. Найти графически корни уравнения 2 х = 2х.

Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х ₁ = 1 и х ₂ = 2. Данное урав­нение имеет два корня х ₁ = 1 и х ₂ = 2 (рис. 6).

Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.

1. Представить указанное уравнение в виде (х) = g (х) с таким расчетом, чтобы функции у=(х) и у = g (х) были просты и удобны для исследования и построения.

2. На бумаге вычертить графики функций у =(х) и у = g (х) в промежутке [а, b ].

3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.

Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.

 Корень уравнения f (х) = 0 считается отделенным на отрезке [ a , b ] , если на этом отрезке уравнение f (х) = 0 не имеет других корней.

 Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.

Отделение корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.

Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.

Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.

1) Если непрерывная на отрезке функция F ( x ) принимает на его концах значения разных знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке единственный.

Рассмотрим примеры поведения некоторых функций:

Рисунок 7

Для отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F ( x )=0, причем можно считать, что все корни находятся на отрезке , в которой функция F ( x ) отделена, непрерывна и F ( A )* F ( B ) F ( x ), начиная с точки X = A , двигаясь вправо с некоторым шагом h .

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X ₁ и X ₂ (Концов выделенных отрезков).

Тема урока: «Решение трансцендентных уравнений»

Цель урока: нахождение корней уравнений математическим способом, проверка решения с помощью компьютера.

Познавательная – применение компьютерных технологий при решении уравнений, использование их при подготовке к ЕГЭ.

Закрепление навыков решения трансцендентных уравнений, проверка знаний учащихся по данной теме.

Развивающая – умение осуществлять взаимосотрудничество, применять знания смежных наук — математики и информатики. Развитие логического мышления учащихся.

Воспитательная – развитие коммуникативных навыков, интереса к учебном предметам. Воспитание ответственного отношения к коллективному труду.

Тип урока: повторительно-обобщающий, межпредметный интегрированный.

Метод: работа группами.

Форма работы: дидактическая игра.

Оборудование : Плакаты, карточки-задания, жетоны, ЭВМ.

1. Организационный момент. Рапорт дежурного командира об отсутствующих

2. Сообщение темы и цели урока.

3. Разминка: а) устный опрос по определениям (математика)

б) решение уравнений по готовым карточкам.

в) устный опрос по определениям (информатика)

4. Решение уравнений в группах за учебным столом и ЭВМ.

5. Оформление протоколов по группам.

6. Подведение итогов (ход урока на доске, оформление газеты-репортажа силами жюри). Награждение победителей соревнования.

7. Домашнее задание. Решить уравнения с использованием ЭВМ (задания ЕГЭ – см приложение “Домашнее задание”)

Класс разбит на три группы, включающие разноуровневый контингент учащихся

1. ПОВТОРЕНИЕ— разминка

а) устный опрос по определениям (каждой из трех команд задается по три вопроса):

1. Определение (уравнения).

Любое выражение вида f (x) = g (x), где f (x) и g (x) – некоторые функции, называется уравнением с одной переменной x (или с одним неизвестным х). Функция f (x) называется левой частью, а g (x) – правой частью уравнения.

2. Определение (корня уравнения).

Число а называется корнем (или решением) данного уравнения с переменной х, если при подстановке числа а вместо х в обе части этого уравнения получаем верное числовое равенство, т.е., если при х = а обе части уравнения определены и их значения совпадают.

3. Что значит решить данное уравнение?

Решить данное уравнение — значит найти множество всех корней (решений) этого уравнения в области R или доказать, что данное уравнение не имеет корней.

4. Определение (числовой функции).

Числовой функцией с областью определения Д называется соответствии, при котором каждому числу х из множества Д сопоставляется по некоторому правилу число у, зависящее от х.

5. Определение (области определения функции), Д(f).

Областью определения функции называется множество значений переменной х при которых функция определена, или существует, или имеет смысл.

6. Определение (области значения функции), Е(f).

Областью значения функции называется множество значений переменной у, которые принимает функция.

7. Определение (графика функции).

Графиком функции f(х) называется множество всех точек (х, у) координатной плоскости, где у = f(х), а х “пробегает” всю область определения функции f(х).

8. Определение (области определения уравнения).

Областью определения уравнения называется общая часть области определения каждой из функций f(x) и g(x) (говорят: пересечение областей определения функций).

9. Определение (трансцендентного уравнения).

Уравнение вида: f(x) = g(x) или v(x) =0, в которых функции f(x), g(x), v(x) показательная, логарифмическая или тригонометрическая принято называть трансцендентными уравнениями.

(Оценка работы — выдача жетона –кружка зелёного цвета –1 балл).

б) решение уравнений по готовым карточкам (каждой из трех команд предлагается решить по три уравнения. Уравнения для каждой команды написаны на небольших плакатах или можно написать на доске. Данные уравнения прилагаются (см приложение “Математическая разминка”).

Свои решения уравнений каждая команда оформляет на местах, а ответы записываются на доске против каждого уравнения. Учитель или консультант проверяет решение и ответ каждого уравнения или показывает учащимся заранее заготовленное решение каждого уравнения.

(Оценка — группе, закончившей работу первой даётся пять баллов, вторым – 4, третьим – 3 балла: жетоны красного цвета-5, синего – 4, жёлтого — 3).

1. Чем определяется положение точки на координатной плоскости ?

2. Таким образом, для построения графика необходимо задать область определения аргумента Х и область значений Y. Как задать область определения аргументов?

(в программе электронных таблиц “Excel” с помощью автозаполнения задать предложенный в задании отрезок изменения значений абсцисс и шаг изменения)

3.Для задания области значений функции необходимо ввести формулу функции. Как записывается формула в ячейке Э.Т.?

(например Y=2X как =2*A3, где A3-адрес ячейки со значением абсциссы)

4. Как быстро ввести эту формулу в таблицу задания значений ординат?

5. Что такое “легенда”? Её назначение?

(область внутри диаграммы с информацией о построенных графиках)

6. Где помещается запись формулы для простоты её расположения в легенде?

(в таблице задания значений Y в первой ячейке в виде текста Y=2X)

7. Где задаётся эта запись?

8. Для активизации “Мастера диаграмм” необходимо задать область адресов ячеек с вычисленными значениями функции, как это сделать?

(в созданной таблице выделить область ячеек со значениями, вызвать “Мастера диаграмм”, в вкладке “Диапазон данных” они автоматически укажутся)

9. Как для “Мастера диаграмм” задать область изменения аргумента для отображения их значений в диаграмме?

(свернуть диалоговое окно, выделить диапазон ячеек со значениями аргументов, при этом курсор должен находиться во вкладке “Ряд” в рамке “Подписи по оси Х”)

(Оценка работы — выдача жетона – кружка зелёного цвета – 1 балл).

б) повторение терминалогии Э.Т. – игра домино по группам

Необходимо сложить ряд из определений (см. приложение “Домино ЭТ”)(Оценка: группе, закончившей работу первой даётся пять баллов, вторым – 4, третьим – 3 балла)

а) Решить уравнение алгебраически, решение оформить на листе (каждое уравнение на отдельном).

б) Используя электронные таблицы (Excel), построить на экране два графика, условие одного слева от знака равенства, другого справа. Точка их пересечения (значение абсциссы) даст корень.

в) Заполнить протокол — отчёт, где указать условие, отрезок значений аргумента (х), шаг его изменения, полученные корни (в процессе алгебраического решения и на ЭВМ ), показав график учителю информатики, сдав листок с решением учителю математики.

Ваши решения будут оценены.

Решение трансцендентных уравнений (протокол)

РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. МЕТОДЫ РЕШЕНИЯ

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

1) Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.

2) Значения f(x) на концах отрезка имеют разные знаки (f(a)×f(b) (x) сохраняют определенный знак на всем отрезке.

Условия 1) и 2) гарантируют, что на интервале [a,b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.

Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.

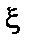
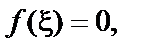Всякое значение , обращающее функцию f(x) в нуль, т.е. такое, что:

называется корнем уравнения (1) или нулем функции f(x).

Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:

1) отделение корней — отыскание приближенного значения корня или содержащего его отрезка;

2) уточнение приближенных корней — доведение их до заданной степени точности.

Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.

Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.

В инженерной практике распространен графический способ определения приближенных корней.

Графический метод отделения корней

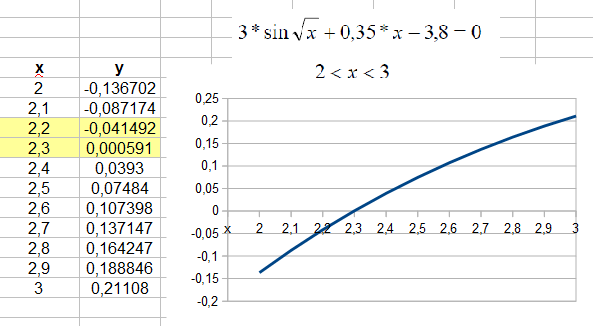
Для отделения корня графическим способом строится график функции f(x)=0 по таблице значений аргументов и функций, где аргумент изменяется с фиксированным шагом. Визуально определяют точку пересечения графика с осью OX. На этом интервале функция меняет знак отрицательный на положительный (рис.1).

Рис.1. Отделение корня графическим способом

Этот интервал изолируют как интервал с единственным возможным корнем. Уравнение может иметь несколько интервалов изоляций и, соответственно, несколько корней.

Рассмотрим методы уточнения приближенных корней в электронной таблице Calc. Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

1. подбора параметра;

2. метод простых итераций;

3. метод половинного деления (метод дихотомии);

4. метод Ньютона (метод касательных);

5. модифицированный метод Ньютона (метод секущих);

6. метод хорд и др.

Подбор параметра

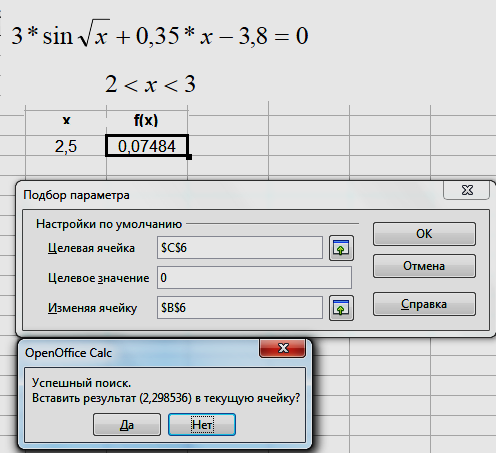
При подборе параметра OOo Calc изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат. Для реализации этого метода нужно в любую ячейку таблицы ввести значение х, принадлежащее интервалу [а,b] (т.е., в пределах отделенного корня). В следующую ячейку ввести значение функции f(x). Затем выбрать команду Сервис\Подбор параметра (рис.2.). В появившемся окне подбора параметра ввести:

• Ячейка с формулой – адрес ячейки с уравнением.

• Целевое значение – результат функции.

• Изменяемая ячейка – адрес ячейки, в которой находится переменная, т.е. х подбираемый из диапазона.

Программа Calc подбирает наиболее подходящий корень и вставляет его в изменяемую ячейку, т.е. вместо х.

Пример решения уравнения методом подбора параметра показан на рис.2.

Рис.2. Метод побора параметра

Дата добавления: 2016-06-15 ; просмотров: 13717 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ