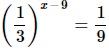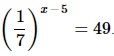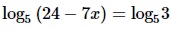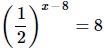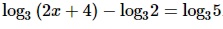Как найти корень уравнения егэ с корнем

Задание №7 ЕГЭ по математике базового уровня

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить

Простейшие (Protozoa) — тип одноклеточных животных.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Вариант 7МБ1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3) 2 = x 2 + 2 · x · 3 + 3 2 = x 2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9) 2 = x 2 – 2 · x · 9 + 9 2 = x 2 – 18x + 81

После преобразования выражение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x 2 + 6x + 9 = x 2 – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 6x – x 2 + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 6x – x 2 + 18x = (x 2 – x 2 ) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ2

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2) 2 = x 2 + 2 · x · 2 + 2 2 = x 2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 8) 2 = x 2 – 2 · x · 8 + 8 2 = x 2 – 16x + 64

После преобразования выражение примет вид:

x 2 + 4x + 4 = x 2 – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую. При переносе из одной части равенства в другую знак меняется на противоположный.

x 2 + 4x – x 2 + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x 2 и x.

x 2 + 4x – x 2 + 16x = (x 2 – x 2 ) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

Решение в общем виде:

Вариант 7МБ3

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_ax + log_ay = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Вариант 7МБ4

Найдите корень уравнения 3 x− 3 = 81.

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

Ответ: 7

Вариант 7МБ5

Найдите корень уравнения log₂( x − 3) = 6 .

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

Вариант 7МБ6

Найдите отрицательный корень уравнения x 2 − x − 6 = 0.

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

Решение:

D = -(1) 2 − 4 • 1 • (-6) = 25

Так как нам необходим отрицательный корень – ответ -2

Вариант 7МБ7

Решите уравнение х 2 = –2х + 24.

Если уравнение имеет больше одного

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

Поскольку требуется указать больший из корней, то ответом будет 4.

Вариант 7МБ8

Найдите корни уравнения 4 х–6 = 64.

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

Вариант 7МБ9

Найдите корень уравнения log₃ (2x – 5) = 2.

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xy n =nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ10

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а) х =а –х .
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ11

Найдите корень уравнения (х – 8) 2 = (х – 2) 2 .

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-

Луб — это сложная проводящая ткань, по которой продукты фотосинтеза (органические вещества) транспортируются из листьев ко всем органам растения (к корневищам, плодам, семенам и т. д.).

Решение:

х 2 – 2 · х ·8 + 8 2 = х 2 – 2 · х · 2 + 2 2

Вариант 7МБ12

Найдите корень уравнения

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а) х =а –х .
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

Вариант 7МБ13

Решите уравнение х 2 – 25 = 0

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

Для ответа берем 5.

Вариант 7МБ14

Найдите корень уравнения

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

Вариант 7МБ15

Найдите корень уравнения

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а) х =а –х .
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

Вариант 7МБ16

Найдите корень уравнения

Задание №1. Простейшие уравнения. Профильный ЕГЭ по математике

В задании №1 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Уравнения, сводящиеся к квадратным

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:

Выбираем меньший корень.

Ответ: — 6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

Условие при этом выполняется.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение

Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

8. Решите уравнение

Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

9. Решите уравнение

Представим в виде степени с основанием 3 и воспользуемся тем, что

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел;

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

11. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

12. Решите уравнение:

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Записываем решение как цепочку равносильных переходов.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: и

Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену Получим:

Получаем решения: Вернемся к переменной x.

Поделим обе части уравнения на и умножим на 4.

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это

15. Решите уравнение В ответе напишите наименьший положительный корень.

Сделаем замену Получим: Решения этого уравнения:

Вернемся к переменной х:

Умножим обе части уравнения на 4 и разделим на

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень

Мы разобрали основные типы уравнений, встречающихся в задании №1 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Алгебра

План урока:

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3