Как найти lim в математике решение уравнений

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Что такое предел функции и как его найти

Общее понятие предела

При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.

А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.

Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.

В нижнюю часть равнобедренного треугольника вписана окружность. Диаметр этой окружности обозначим как . На рисунке диаметр проведён синим цветом. К окружности параллельно основанию первоначального треугольника проведена касательная (она на рисунке серого цвета). В результате получен треугольник, подобный первоначальному. В этот треугольник точно так же вписана окружность. Её диаметр — (диаметры на рисунке ограничены касательными). Аналогичные построения продолжаются, пока позволяет высота треугольника. Получена последовательность уменьшающихся окружностей и соответствующая им последовательность длин их диаметров: . Эта последовательность длин диаметров даёт пример переменной величины , которая с возрастанием номера окружности x неограниченно приближается к нулю. Предел этой последовательности равен нулю: .

Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле

Величина, которую нам требуется найти, будет записана так:

Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.

Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется «доопределить функцию», с этим определением вы можете ознакомиться в последующих частях главы «Предел»). Примем, что конечная величина, поделенная на бесконечность, равна нулю:

С рассмотренной последовательностью окружностей свяжем другую переменную величину — последовательность сумм их диаметров:

Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.

Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.

Предел функции

Предел функции при

Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :

(1)

сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность

(2)

и можно ставить вопрос о существовании её предела.

Определение 1. Число A называется пределом функции f(x) в точке (или при ), если для любой сходящейся к последовательности (1) значений аргумента x, отличных от , соответствующая последовательность (2) сходится к числу A.

Символически это записывается так:

Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.

Пример 1. Найти предел функции при .

Решение. Подставляем вместо x значение 0. Получаем:

.

Итак, предел данной функции при равен 1.

Кроме того, решённые в этом уроке примеры и любые другие задачи на пределы, можно на проверить на калькуляторе пределов онлайн.

Предел функции при , при и при

Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 2. Число A называется пределом функции f(x) при , если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: .

Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: ().

Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.

Пример 2. Найти предел функции при .

Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:

.

Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Основные теоремы о пределах

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

(3)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(4)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

(5)

Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

Пример 3. Найти предел:

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 4. Найти предел:

Решение. Предварительно убедимся, что предел делителя не равен нулю:

Таким образом, формула (5) применима и, значит,

А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функция f(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.

Пример 5. Найти предел:

Решение. Теорема о пределе частного здесь неприменима, так как

Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим

корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:

Найти предел самостоятельно, а затем посмотреть решение

Пример 6. Найти предел:

Пример 7. Найти предел:

.

Пример 8. Найти предел:

.

Пример 9. Найти предел:

.

Пример 10. Найти предел:

.

Пример 11. Найти пределы:

Решение пределов через раскрытие неопределённостей

При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида — самые распространённые неопределённости, которые требуется раскрывать при решении пределов.

БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.

Освоим эти приёмы на примерах.

Неопределённость вида

Пример 12. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :

.

Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или «супермалому числу».

Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 13. Раскрыть неопределённость и найти предел .

Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:

.

Комментарий к ходу решения. В числителе загоняем «икс» под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо «икса».

Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Неопределённость вида

Пример 14. Раскрыть неопределённость и найти предел .

Решение. В числителе — разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:

.

В знаменателе — квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

Запишем выражение, полученное в результате преобразований и найдём предел функции:

Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.

Пример 15. Раскрыть неопределённость и найти предел

Решение. Теорема о пределе частного здесь неприменима, поскольку

Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

Пример 16. Раскрыть неопределённость и найти предел

Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:

Раскрыть неопределённости самостоятельно, а затем посмотреть решения

Пример 17. Раскрыть неопределённость и найти предел

.

Пример 18. Раскрыть неопределённость и найти предел

.

Пример 19. Раскрыть неопределённость и найти предел

.

Что означает предел в математике

Сага о погрешностях при участии слова lim

Кто о чём, а мы продолжаем разбирать сложную математику, чтобы она не была такой сложной.

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

1. Есть функция — это просто какая-то «коробка» с математикой. Ты ей на вход число, она его обрабатывает у себя внутри и отдаёт другое число.
2. У функции есть как минимум два числа: то, которое ты ей даёшь на вход; и то, которое получаешь на выходе.
3. Иногда математикам интересно, что будет, если число на входе будет к чему-то стремиться. А именно: «Если число на входе будет стремиться вот сюда, куда будет стремиться число на выходе?»

Самое простое объяснение функции в математике.

👉 Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

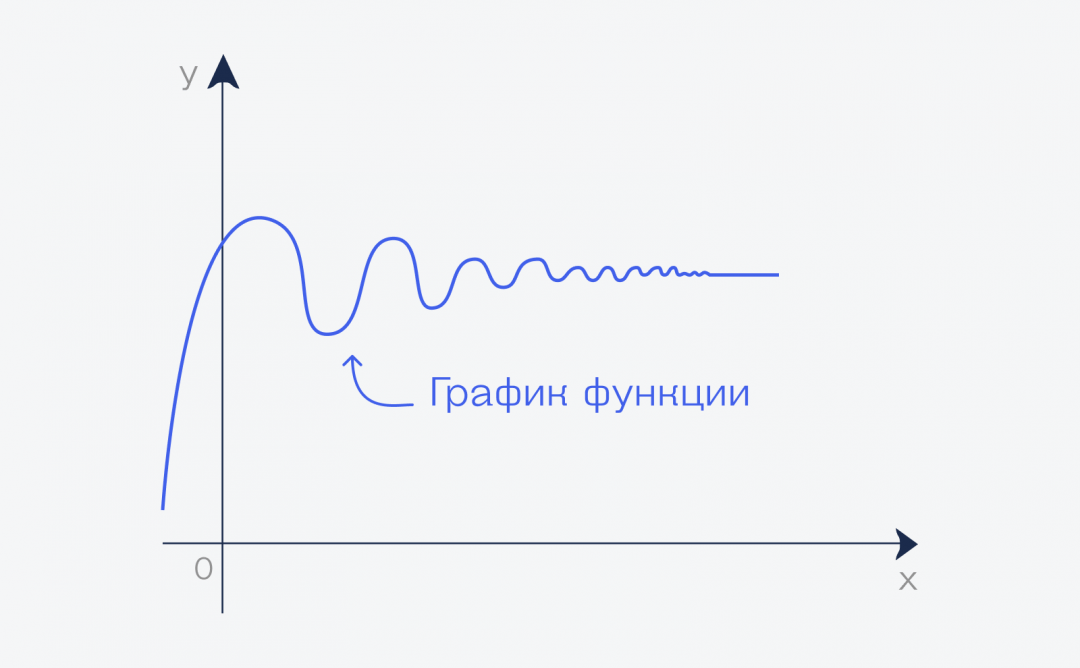
График и предел

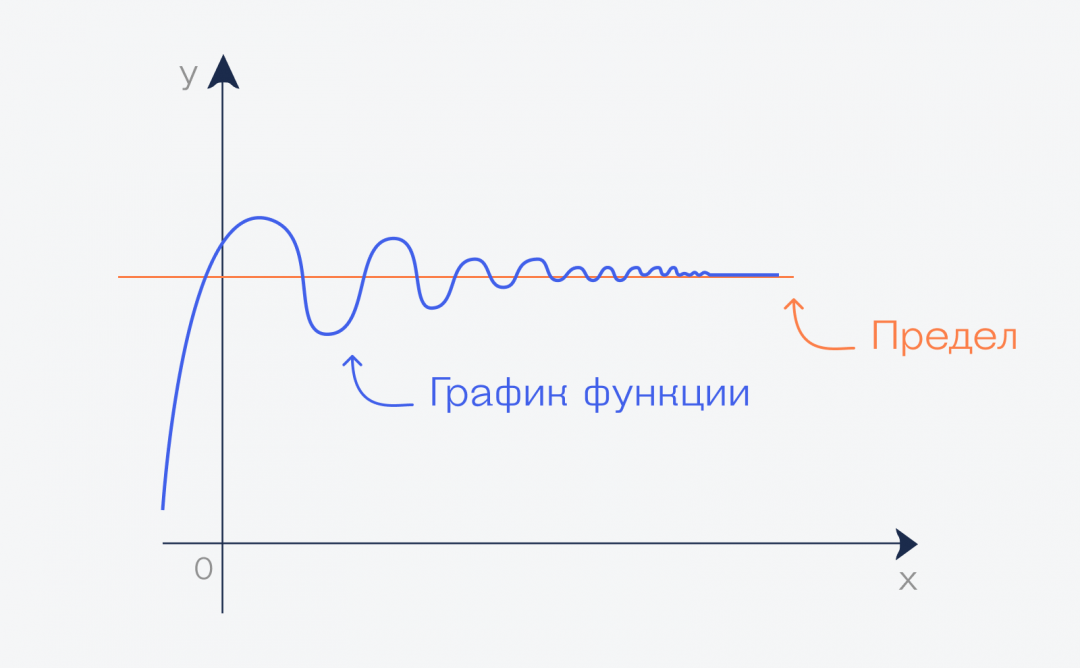
Если мы нарисуем график этой функции, то можем увидеть, что начиная с какого-то момента он превратится в почти прямую линию вдоль оси. Почти прямую — потому что прямой он никогда не станет, но стремится к этому, если продолжить рисовать график бесконечно.

Но бесконечный график означает, что у нас переменная функции стремится к бесконечности. А значение этой линии на графике — это и есть предел этой функции при переменной, стремящейся к бесконечности:

Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

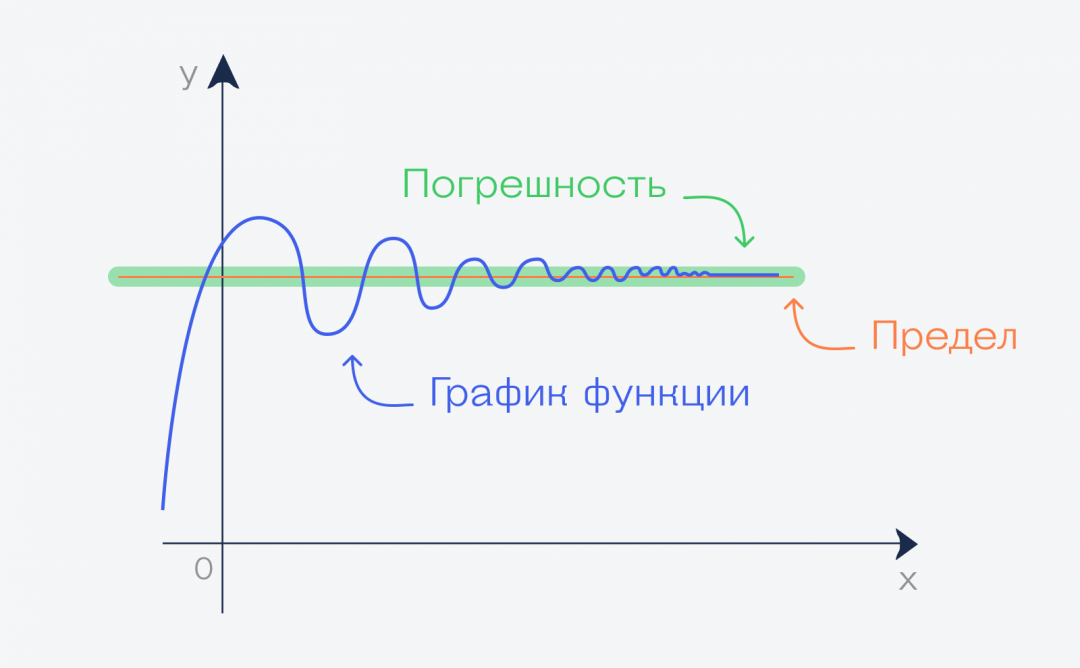
Погрешность в пределах

В математике пределы считаются точно: используются специальные формулы и трюки, которые помогают найти точный ответ. Но в жизни такая точность необязательна: можно взять любое решение, которое нас устроит с приемлемой погрешностью.

Эта погрешность поможет нам считать пределы, не зная точных математических формул подсчёта.

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

1. Закончилось количество повторений. Например, мы заранее говорим, что будем стремиться к границе предела 10000000000 раз, но если ничего не выйдет — остановимся.
2. Если достигли нужной погрешности. Два соседних результата отличаются на величину погрешности или меньше — отлично, мы нашли то, что нужно.

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

⚠️ Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

Например, если мы дали переменной 32 бита памяти, самое малое число, которое мы сможем в нее записать, — 1,4012985 × 10 -45 . Это кажется бесконечно малым, но на самом деле, если циклически делить число на 2 несколько сотен раз в секунду, мы упремся в этот лимит точности почти сразу. Потом знаки после запятой закончатся и число очень быстро превратится в 0.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность.

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

• предел функции f(x) = (8−2x) / (x²−4x-12);
• при x стремящемся к 2.

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

Программа справилась и выдала результат с нужной нам точностью