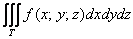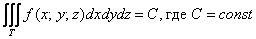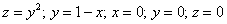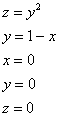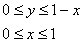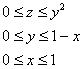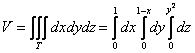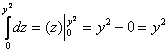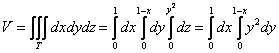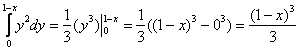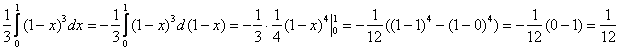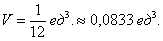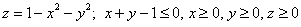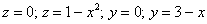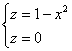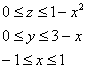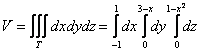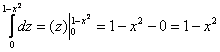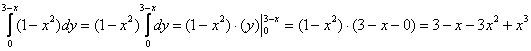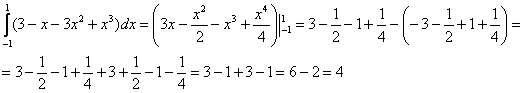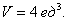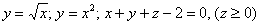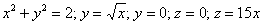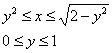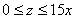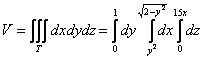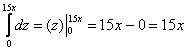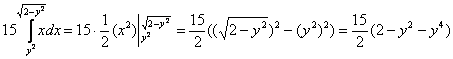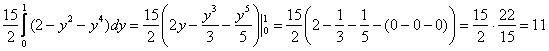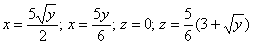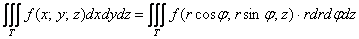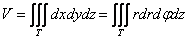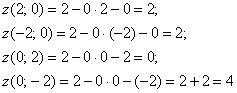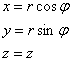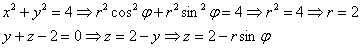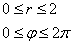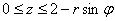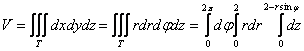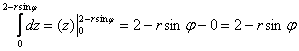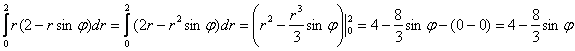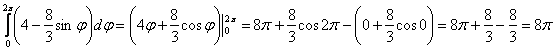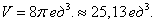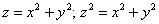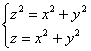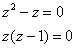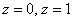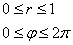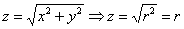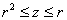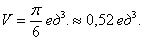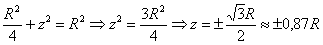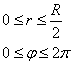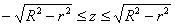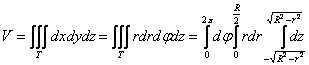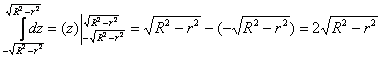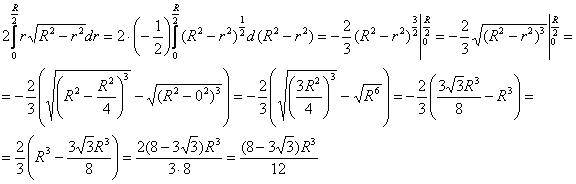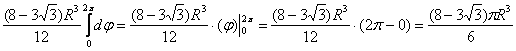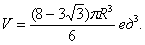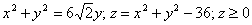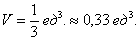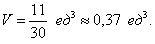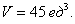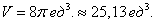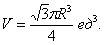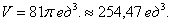Вычисление объёмов
Вычисление объёмов
- Услуги проектирования
- Двойной интеграл
- Вычисление объёмов
Вычисление объёмов
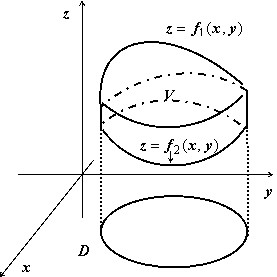
Объём тела, ограниченного сверху и снизу поверхностями $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 1 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $\mathbf < \textit < z >> =\mathbf < \textit < f >> _ < 2 >(\mathbf < \textit < x >> $,$\mathbf < \textit < y >> )$, $(x,y)\in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $\mathbf < \textit < Oz >> $, равен $v=\iint\limits_D < \left[ < f_1 (x,y)-f_2 (x,y) >\right]dxdy > $; эта формула очевидно следует из геометрического смысла двойного интеграла.
Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.
Найти объём тела $V:\left[ < \begin
Решение:
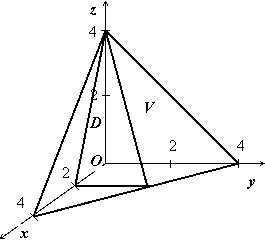
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $\mathbf < \textit < Oxz >> $:
$V:\left[ < \begin
Область $\mathbf < \textit < D >> $ — треугольник, ограниченный прямыми $\mathbf < \textit < x >> $ = 0, $\mathbf < \textit < z >> $ = 0, 2$\mathbf < \textit < x >> +\mathbf < \textit < z >> $ = 4, поэтому
Найти объём области, ограниченной поверхностями $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < R >> ^ < 2 >$,
Решение:
Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $\mathbf < \textit < Oz >> $ < в уравнении нет $\mathbf < \textit < z >> $ в явной форме). Построить в плоскости $\mathbf < \textit < Oxy >> $ кривую шестого порядка, заданную уравнением $(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)^ < 3 >=\mathbf < \textit < R >> ^ < 2 >(\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >)$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей < чётные степени >и точка $\mathbf < \textit < О >> (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(\cos ^4\varphi +\sin ^4\varphi );r^2=R^2((\cos ^2\varphi +\sin ^2\varphi )^2-2\cos ^2\varphi \sin ^2\varphi )=R^2(1-\frac < \sin ^22\varphi > < 2 >)=$
$=R^2(1-\frac < 1-\cos 4\varphi > < 4 >)=R^2\frac < 3+\cos 4\varphi > < 4 >;r=R\frac < \sqrt < 3+\cos 4\varphi >> < 2 >.$ Эту кривую построить уже можно. $r(\varphi )$ максимально, когда $\cos 4\varphi =1\;(\varphi =0,\frac < 2\pi > < 4 >=\frac < \pi > < 2 >,\frac < 4\pi > < 4 >=\pi ,\frac < 6\pi > < 4 >=\frac < 3\pi > < 2 >)$, минимально, когда
$\cos 4\varphi =-1\;(\varphi =\frac < \pi > < 4 >,\frac < 3\pi > < 4 >,\frac < 5\pi > < 4 >,\frac < 7\pi > < 4 >),$ и гладко меняется между этими пределами < точка $\mathbf < \textit < О >> (0,0)$ не принадлежит этой кривой, где мы её потеряли? > .
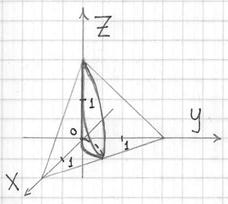
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)
Решение:
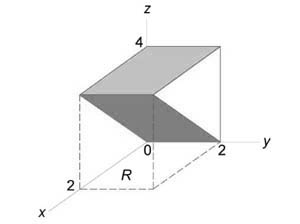
Данное тело показано на рисунке.
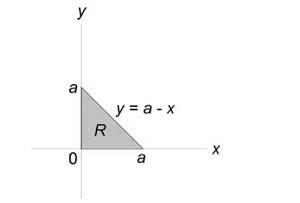
Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ < V = \iint\limits_R < \left[ < \left( < 4 - x >\right) — x >\right]dxdy > > = < \int\limits_0^2 < \left[ < \int\limits_0^2 < \left( < 4 - 2x >\right)dy > >\right]dx > > = < \int\limits_0^2 < \left[ < \left. < \left( < 4y - 2xy >\right) >\right|_ < y = 0 >^2 >\right]dx > > = < \int\limits_0^2 < \left( < 8 - 4x >\right)dx > > = < \left. < \left( < 8x - 2 < x^2 >>\right) >\right|_0^2 > = < 16 - 8 = 8. >$
Описать тело, объем которого определяется интегралом (V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > .)
Решение:
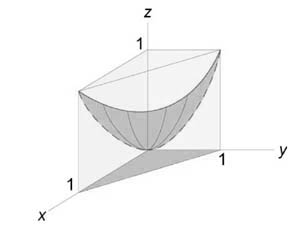
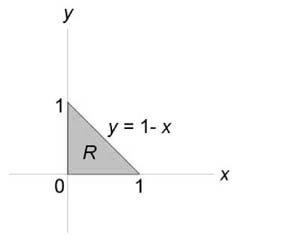
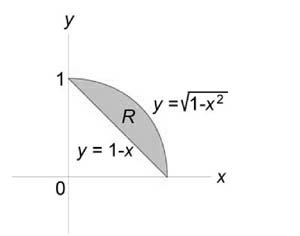
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = < x^2 >+ < y^2 >.) Объем тела равен $ < V = \int\limits_0^1 < dx >\int\limits_0^ < 1 - x > < \left( < < x^2 >+ < y^2 >>\right)dy > > = < \int\limits_0^1 < \left[ < \left. < \left( < < x^2 >y + \frac < < < y^3 >> > < 3 >>\right) >\right|_ < y = 0 >^ < 1 - x >>\right]dx > > = < \int\limits_0^1 < \left[ < < x^2 >\left( < 1 - x >\right) + \frac < < < < \left( < 1 - x >\right) > ^3 > > > < 3 >>\right]dx > > = \\ = < \int\limits_0^1 < \left( < < x^2 >— < x^3 >+ \frac < < 1 - 3x + 3 < x^2 >— < x^3 >> > < 3 >>\right)dx > > = < \int\limits_0^1 < \left( < 2 < x^2 >— \frac < < 4 < x^3 >> > < 3 >— x + \frac < 1 > < 3 >>\right)dx > > = < \left. < \left( < \frac < < 2 < x^3 >> > < 3 >— \frac < 4 > < 3 >\cdot \frac < < < x^4 >> > < 4 >— \frac < < < x^2 >> > < 2 >+ \frac < x > < 3 >>\right) >\right|_0^1 > = < \frac < 2 > < 3 >— \frac < 1 > < 3 >— \frac < 1 > < 2 >+ \frac < 1 > < 3 >= \frac < 1 > < 6 >. > $
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)
Решение:
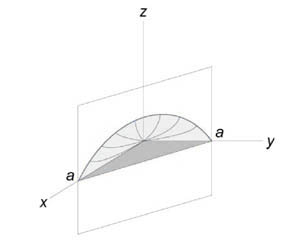
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( < x^2 >+ < y^2 >= 1,) (z = 1 — x.)
Решение:
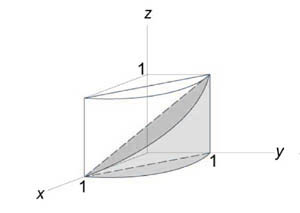
Как видно из рисунков, в области интегрирования (R) при (0 \le x \le 1) значения (y) изменяются от (1 — x) до (\sqrt < 1 - < x^2 >> .)
Вычислим второй интеграл ( < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > ,) используя замену переменной. Полагаем (1 — < x^2 >= w.) Тогда (-2xdx = dw) или (xdx = \large\frac < < - dw >> < 2 >\normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ < < I_2 >= \int\limits_0^1 < x\sqrt < 1 - < x^2 >> dx > > = < \int\limits_1^0 < \sqrt w \left( < - \frac < < dw >> < 2 >>\right) > > = < - \frac < 1 > < 2 >\int\limits_1^0 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < \sqrt w dw >> = < \frac < 1 > < 2 >\int\limits_0^1 < < w^ < \large\frac < 1 > < 2 >\normalsize > > dw > > = < \frac < 1 > < 2 >\left. < \left( < \frac < < 2 < w^ < \large\frac < 3 > < 2 >\normalsize > > > > < 3 >>\right) >\right|_0^1 = \frac < 1 > < 3 >. > $ Наконец, вычислим третий интеграл. $\require < cancel > < < I_3 >= \int\limits_0^1 < \left( < 1 - 2x + < x^2 >>\right)dx > > = < \left. < \left( < x - < x^2 >+ \frac < < < x^3 >> > < 3 >>\right) >\right|_0^1 > = < \cancel < 1 >— \cancel < 1 >+ \frac < 1 > < 3 >= \frac < 1 > < 3 >. > $ Таким образом, объем тела равен $ < V = < I_1 >— < I_2 >— < I_3 >> = < \frac < \pi > < 4 >— \frac < 1 > < 3 >— \frac < 1 > < 3 >= \frac < \pi > < 4 >— \frac < 2 > < 3 >\approx 0,12. > $
Вычислить объем единичного шара.
Решение:
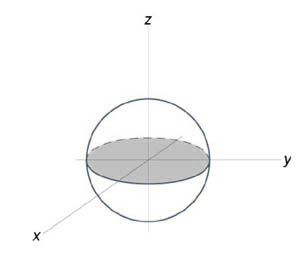
Уравнение сферы радиусом (1) имеет вид ( < x^2 >+ < y^2 >+ < z^2 >= 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = \sqrt < 1 - \left( < < x^2 >+ < y^2 >>\right) > .$ Преобразуя это уравнение в полярные координаты, получаем $z\left( < r,\theta >\right) = \sqrt < 1 - < r^2 >> .$ В полярных координатах область интегрирования (R) описывается множеством (R = \left[< \left( < r,\theta >\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi >\right].) Следовательно, объем верхнего полушара выражается формулой $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = \iint\limits_R < \sqrt < 1 - < r^2 >> rdrd\theta > > = < \int\limits_0^ < 2\pi > < d\theta >\int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > . > $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — < r^2 >= t.) Тогда (-2rdr = dt) или (rdr = — \large\frac < < dt >> < 2 >\normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ < < V_ < \large\frac < 1 > < 2 >\normalsize > > = 2\pi \int\limits_0^1 < \sqrt < 1 - < r^2 >> rdr > > = < 2\pi \int\limits_1^0 < \sqrt t \left( < - \frac < < dt >> < 2 >>\right) > > = < - \pi \int\limits_1^0 < \sqrt t dt >> = < \pi \int\limits_0^1 < < t^ < \large\frac < 1 > < 2 >\normalsize > > dt > > = < \pi \left. < \left( < \frac < < < t^ < \large\frac < 3 > < 2 >\normalsize > > > > < < \frac < 3 > < 2 >> > >\right) >\right|_0^1 > = < \frac < < 2\pi >> < 3 >. > $ Таким образом, объем единичного шара равен $V = 2 < V_ < \large\frac < 1 > < 2 >\normalsize > > = \frac < < 4\pi >> < 3 >.$
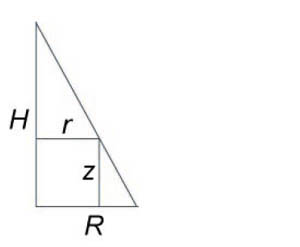
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).
Решение:
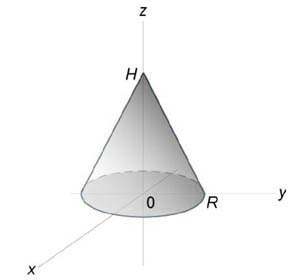
Далее:
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Вычисление объёмов
Теорема об аналоге СДНФ в Pk
Свойства тройного интеграла
Равносильные формулы алгебры высказываний
Дифференциальные характеристики векторного поля
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Критерий полноты <формулировка>. Лемма о несамодвойственной функции
Лемма о построении множества $[F]_
Булевы функции от $n$ переменных
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Выражение площади плоской области через криволинейный интеграл
Определение двойного интеграла
Соленоидальное векторное поле
Огравление $\Rightarrow $
Тройные интегралы. Вычисление объема тела.
Тройной интеграл в цилиндрических координатах
Три дня в деканате покойник лежал, в штаны Пифагора одетый,
В руках Фихтенгольца он томик держал, что сжил его с белого света,
К ногам привязали тройной интеграл, и в матрицу труп обернули,
А вместо молитвы какой-то нахал прочёл теорему Бернулли.
Тройные интегралы – это то, чего уже можно не бояться =) Ибо если Вы читаете сей текст, то, скорее всего, неплохо разобрались с теорией и практикой «обычных» интегралов, а также двойными интегралами. А там, где двойной, неподалёку и тройной:
И в самом деле, чего тут опасаться? Интегралом меньше, интегралом больше….
Разбираемся в записи:
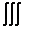
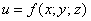
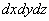
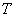
Особо остановимся на области интегрирования. Если в двойном интеграле она представляет собой плоскую фигуру, то здесь – пространственное тело, которое, как известно, ограничено множеством поверхностей. Таким образом, помимо вышеуказанного вы должны ориентироваться в основных поверхностях пространства и уметь выполнять простейшие трёхмерные чертежи.
Некоторые приуныли, понимаю…. Увы, статью нельзя озаглавить «тройные интегралы для чайников», и кое-что знать/уметь нужно. Но ничего страшного – весь материал изложен в предельно доступной форме и осваивается в кратчайшие сроки!
Что значит вычислить тройной интеграл и что это вообще такое?
Вычислить тройной интеграл – это значит найти ЧИСЛО:
В простейшем случае, когда 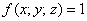
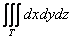
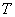
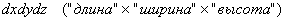
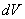
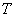
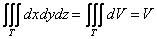
Кроме того, у тройного интеграла есть важные физические приложения. Но об этом позже – во 2-й части урока, посвящённой вычислениям произвольных тройных интегралов, у которых функция 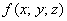
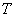
Как решить тройной интеграл?
Ответ логично вытекает из предыдущего пункта. Необходимо определить порядок обхода тела и перейти к повторным интегралам. После чего последовательно расправиться с тремя одиночными интегралами.
Как видите, вся кухня очень и очень напоминает двойные интегралы, с тем отличием, что сейчас у нас добавилась дополнительная размерность (грубо говоря, высота). И, наверное, многие из вас уже догадались, как решаются тройные интегралы.
Развеем оставшиеся сомнения:
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
Пожалуйста, перепишите столбиком на бумагу:
И ответьте на следующие вопросы. Знаете ли Вы, какие поверхности задают эти уравнения? Понятен ли Вам неформальный смысл этих уравнений? Представляете ли Вы, как данные поверхности расположены в пространстве?
Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте урок Основные поверхности пространства, иначе дальше будет не продвинуться!
Решение: используем формулу 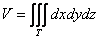
Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертёжи.
По условию тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий:
Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость 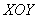
Коль скоро проецирование проводится вдоль оси 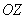
– уравнение 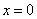
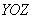
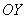
– уравнение 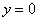
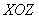
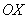
– уравнение 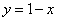
Скорее всего, искомая проекция представляет собой следующий треугольник: 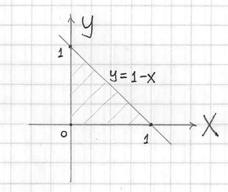
Возможно, не все до конца поняли, о чём речь. Представьте, что из экрана монитора выходит ось 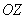
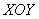
Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего», «вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в начале координат радиусом мЕньшим единицы, например, сфера 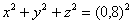
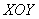
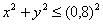
На втором этапе выясняем, чем тело ограничено сверху, чем снизу и выполняем пространственный чертёж. Возвращаемся к условию задачи и смотрим, какие поверхности остались. Уравнение 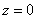
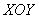
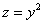
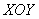
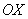
Кстати, здесь обнаружилась избыточность условия – в него было не обязательно включать уравнение плоскости 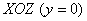
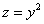
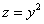
Аккуратно изобразим фрагмент параболического цилиндра: 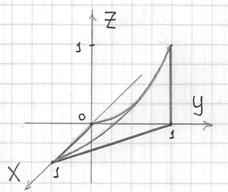
После выполнения чертежей с порядком обхода тела никаких проблем!
Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ ориентироваться по двумерному чертежу). Это делается АБСОЛЮТНО ТАК ЖЕ, как и в двойных интегралах! Вспоминаем лазерную указку и сканирование плоской области. Выберем «традиционный» 1-й способ обхода:
Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем пациента. Лучи входят в тело через плоскость 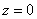
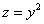
Перейдём к повторным интегралам:
С интегралами опять рекомендую разбираться по отдельности:
1) Начать следует с «зетового» интеграла. Используем формулу Ньютона-Лейбница:
Подставим результат в «игрековый» интеграл:
Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле 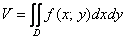
2)
3)
Обратите внимание на рациональную технику решения 3-го интеграла.
Ответ:
Вычисления всегда можно записать и «одной строкой»: 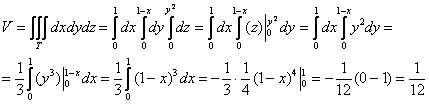
Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов допустить ошибку.
Ответим на важный вопрос:
Нужно ли делать чертёжи, если условие задачи не требует их выполнения?
Можно пойти четырьмя путями:
1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа, не ленитесь, делайте оба чертежа. Рекомендую в первую очередь.
2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот способ я бы советовал только людям с хорошим уровнем подготовки.
3) Изобразить только проекцию. Тоже неплохо, но тогда обязательны дополнительные письменные комментарии, чем ограничена область с различных сторон. К сожалению, третий вариант зачастую бывает вынужденным – когда тело слишком велико либо его построение сопряжено с иными трудностями. И такие примеры мы тоже рассмотрим.
4) Обойтись вообще без чертежей. В этом случае нужно представлять тело мысленно и закомментировать его форму/расположение письменно. Подходит для совсем простых тел либо задач, где выполнение обоих чертежей затруднительно. Но всё же лучше сделать хотя бы схематический рисунок, поскольку «голое» решение могут и забраковать.
Следующее тело для самостоятельного дела:
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество неравенств 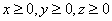
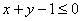
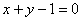
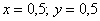
Примерный образец оформления задачи в конце урока.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.
Решение: формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая.
Придерживаемся отработанной ранее тактики – сначала разберёмся с поверхностями, которые параллельны оси аппликат. Уравнения таких поверхностей не содержат в явном виде переменную «зет»:
– уравнение 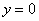
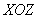
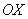
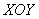
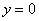
– уравнение 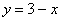
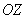
Но две прямые 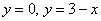
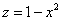
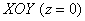
Подставим 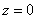
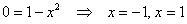
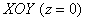
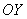
Изобразим проекцию тела на плоскость 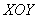
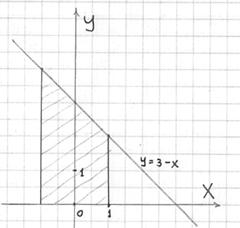
Ещё раз призываю! – если остаётся какое-то недопонимание по выполнению чертежей и/или объяснениям, обращайтесь к справочной статье Основные поверхности пространства и в тяжёлом случае – к урокам Уравнение прямой на плоскости, Уравнение плоскости.
Искомое тело ограниченно плоскостью 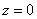
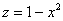
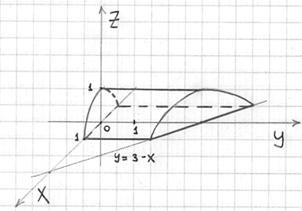
Составим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования, напоминаю, удобнее выяснять по двумерному чертежу:
Таким образом:
1)
2)
При интегрировании по «игрек» – «икс» считается константой, поэтому константу 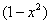
3)
Ответ:
Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом, поскольку с большой вероятностью возникнет иллюзия объёма, о которой я рассказал ещё на уроке Объем тела вращения. Так, оценивая тело рассмотренной задачи, лично мне показалось, что в нём гораздо больше 4 «кубиков».
Следующий пример для самостоятельного решения:
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость 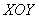
Примерный образец оформления задачи в конце урока.
Не редкость, когда выполнение трёхмерного чертежа затруднено:
С помощью тройного интеграла найти объём тела, заданного ограничивающими его поверхностями
Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если выбрать 1-й способ, то фигуру придётся разделить на 2 части, что неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим 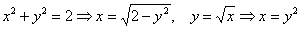
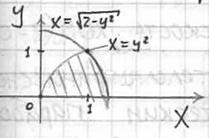
Прошу прощения за качество некоторых картинок, я их вырезаю прямо из собственных рукописей.
Выбираем более выгодный порядок обхода фигуры:
Теперь дело за телом. Снизу оно ограничено плоскостью 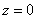
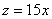
Но есть и третий, исконно русский метод решения проблемы – забить =) А вместо трёхмерного чертежа обойтись словесным описанием: «Данное тело ограничено цилиндрами 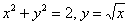
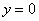
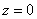
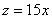
«Вертикальные» пределы интегрирования, очевидно, таковы:
Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом:
1)
2)
3)
Ответ:
Как вы заметили, предлагаемые в задачах тела не дороже сотни баксов часто ограничены плоскостью 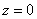
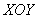
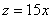
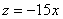
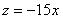
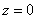
Легко убедиться, что получится тот же самый результат: 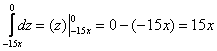
(помним, что тело нужно обходить строго снизу вверх!)
Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше плоскости 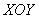
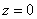
Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения:
С помощью тройного интеграла найти объём тела, ограниченного поверхностями
Краткое решение и ответ в конце урока.
Переходим ко второму параграфу с не менее популярными материалами:
Тройной интеграл в цилиндрических координатах
Цилиндрические координаты – это, по сути, полярные координаты в пространстве.
В цилиндрической системе координат положение точки 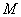
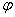
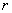
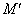
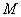
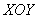
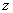
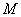
Переход от трёхмерной декартовой системы к цилиндрической системе координат осуществляется по следующим формулам:
Применительно к нашей теме преобразование выглядит следующим образом:
И, соответственно, в упрощённом случае, который мы рассматриваем в этой статье:
Главное, не забывать про дополнительный множитель «эр» и правильно расставлять полярные пределы интегрирования при обходе проекции:
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями 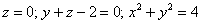
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности 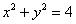
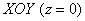
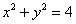
Плоскости 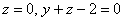
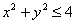
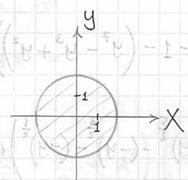
На очереди трёхмерный чертёж. Основная трудность состоит в построении плоскости 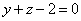
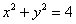
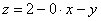
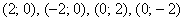
Отмечаем найдённые точки на чертеже и аккуратно (а не так, как я =)) соединяем их линией: 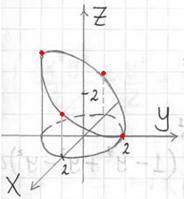
Проекция тела на плоскость 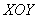
Найдём уравнения поверхностей в цилиндрических координатах:
Теперь следует выяснить порядок обхода тела.
Сначала разберёмся с проекцией. Как определить её порядок обхода? ТОЧНО ТАК ЖЕ, как и при вычислении двойных интегралов в полярных координатах. Здесь он элементарен:
«Вертикальные» пределы интегрирования тоже очевидны – входим в тело через плоскость 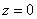
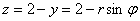
Перейдём к повторным интегралам:
При этом множитель «эр» сразу ставим в «свой» интеграл.
Веник как обычно легче сломать по прутикам:
1)
Сносим результат в следующий интеграл:
2)
А тут не забываем, что «фи» считается константой. Но это до поры до времени:
3)
Ответ:
Похожее задание для самостоятельного решения:
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями 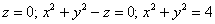
Примерный образец чистового оформления в конце урока.
Обратите внимание, что в условиях задач ни слова не сказано о переходе к цилиндрической системе координат, и несведущий человек будет бодаться с трудными интегралами в декартовых координатах. …А может и не будет – ведь есть третий, исконно русский способ решения проблем =)
Всё только начинается! …в хорошем смысле: =)
С помощью тройного интеграла найти объем тела, ограниченного поверхностями
Скромно и со вкусом.
Решение: данное тело ограничено конической поверхностью 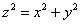
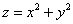
Сначала найдём линии, по которым пересекаются поверхности. Составим и решим следующую систему:
Из 1-го уравнения почленно вычтем второе:
В результате получено два корня:
Подставим найденное значение 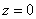
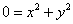
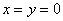
Таким образом, корню 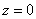
Теперь подставим второй корень 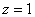
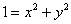
Каков геометрический смысл полученного результата? «На высоте» 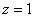
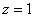
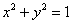
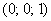
При этом «чаша» параболоида вмещает в себя «воронку» конуса, поэтому образующие конической поверхности следует прочертить пунктиром (за исключением отрезка дальней от нас образующей, который виден с данного ракурса): 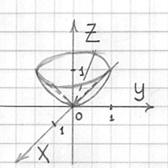
Проекцией тела на плоскость 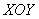
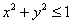
При переходе к цилиндрическим координатам по стандартным формулам неравенство запишется в простейшем виде 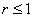
Найдём уравнения поверхностей в цилиндрической системе координат: 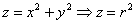
Так как в задаче рассматривается верхняя часть конуса, то из уравнения 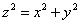
«Сканируем тело» снизу вверх. Лучи света входят в него через эллиптический параболоид 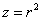
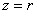
Остальное дело техники:
Ответ:
Не редкость, когда тело задаётся не ограничивающими его поверхностями, а множеством неравенств:
С помощью тройного интеграла вычислить объём заданного тела: 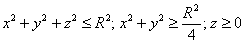
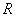
Геометрический смысл пространственных неравенств я достаточно подробно разъяснил в той же справочной статье – Основные поверхности пространства и их построение.
Данная задача хоть и содержит параметр, но допускает выполнение точного чертежа, отражающего принципиальный вид тела. Подумайте, как выполнить построение. Краткое решение и ответ – в конце урока.
…ну что, ещё парочку заданий? Думал закончить урок, но прямо так и чувствую, что вы хотите ещё =)
С помощью тройного интеграла вычислить объём заданного тела: 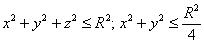
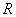
Решение: неравенство 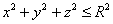
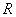
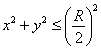
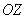
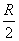
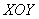
Принимая 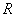
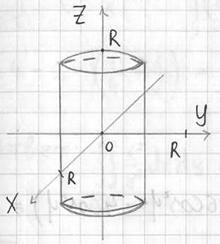
Точнее, его следует назвать рисунком, поскольку пропорции по оси 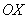
Обратите внимание, что здесь не обязательно выяснять высоту, на которой цилиндр высекает из шара «шапки» – если взять в руки циркуль и наметить им окружность с центром в начале координат радиуса 2 см, то точки пересечения с цилиндром получатся сами собой.
Кстати, как найти эту высоту аналитически? Нужно подставить сумму квадратов 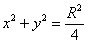
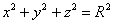
Но вернёмся к теме. Проекция данного тела на плоскость 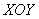
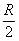
По формулам перехода 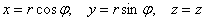
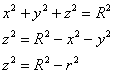
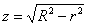
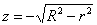
Лучи «лазера» входят в тело через нижнюю «шапку» и выходят через верхнюю, таким образом:
Можно сослаться на симметрию и вычислить объём половины тела, но, как ни странно, это только заморочит решение – гораздо проще провести формальные вычисления.
Расписываем и щёлкаем повторные интегралы:
1)
Вот так – и никаких комментов о симметрии. Сносим результат в следующий интеграл:
2)
Здесь в целях сократить решение я подвёл функцию под знак дифференциала, но «чайникам» всё же рекомендую «классический» путь замены переменной.
Сносим полученную константу в последний интеграл, а точнее, сразу выносим её за его пределы:
3)
Ответ:
Косвенным признаком правильности вычислений является тот факт, что параметр вошёл в ответ в кубе. Ну и ещё на всякий пожарный, проверим, не получился ли случаем результат отрицательным: 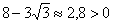
Заключительное задание для самостоятельного решения:
С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями
Особенность этого примера состоит в том, что здесь затруднено построение трёхмерного чертежа (уже знакомый из предыдущего параграфа мотив) и в этой связи тело придётся представить мысленно. Да и проекция, к слову, тоже не сахар.
В данную статью я включил не самые сложные примеры, и желающие могут закачать дополнительные задачи с готовыми решениями, в частности, интересны и поучительны примеры, где тело приходится разделять на 2 части.
Ну а сейчас я предлагаю сделать передышку и ознакомиться с заключительной частью урока – Как вычислить произвольный тройной интеграл?
Решения и ответы:
Пример 2: Решение: изобразим данное тело на чертеже. 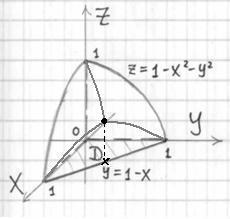
Примечание: при 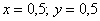
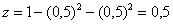
Порядок обхода тела: 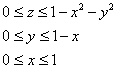
Объём тела вычислим с помощью тройного интеграла: 
Ответ:
Пример 4: Решение: изобразим проекцию данного тела на плоскость 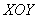
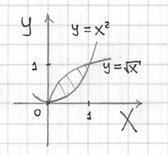
Данное тело ограничено параболическими цилиндрами сбоку, плоскостью 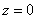
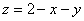
Выберем следующий порядок обхода тела: 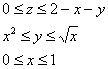
Таким образом: 
Ответ:
Пример 6: Решение: изобразим проекцию данного тела на плоскость 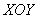
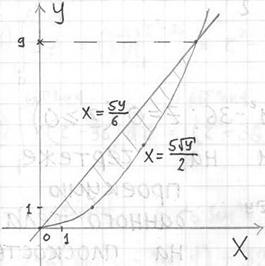
Данное тело ограничено параболическим цилиндром 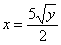
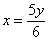
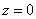
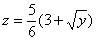
Примечание: обратите внимание, что 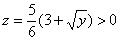
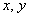
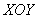
Выберем следующий порядок обхода тела: 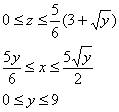
Вычислим объём тела: 
Ответ:
Пример 8: Решение: данное тело ограничено плоскостью 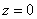
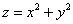
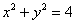
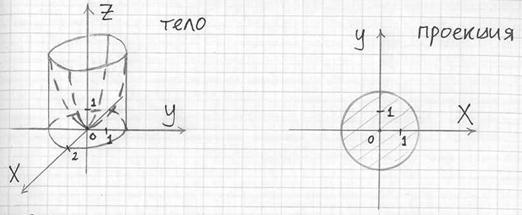
Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат: 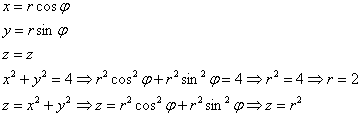
Порядок обхода тела: 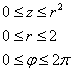
Таким образом: 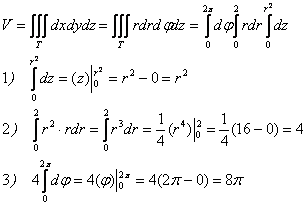
Ответ:
Пример 10: Решение: данное тело ограничено плоскостью 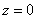
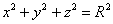
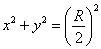
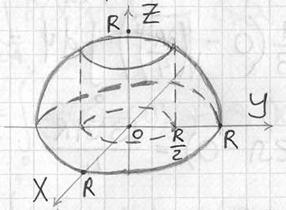
Проекция тела на плоскость 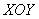
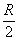
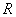
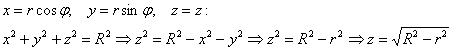
Порядок обхода тела: 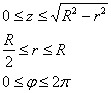
Таким образом: 
Ответ:
Пример 12: Решение: изобразим проекцию данного тела на плоскость 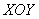
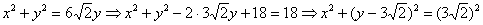
Проекцией цилиндра 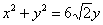
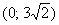
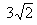
Найдём линию пересечения эллиптического параболоида с плоскостью 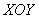
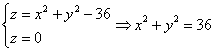
Выполним чертёж: 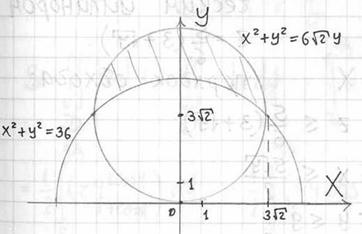
Искомое тело ограничено плоскостью 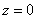
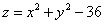
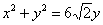
Объём тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат: 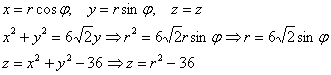
Порядок обхода тела: 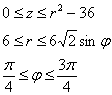
Таким образом:
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

Как найти объем тела заданного уравнениями
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
http://mathprofi.net/troinye_integraly.html
http://reshka.feniks.help/vysshaya-matematika/integraly/vychislit-obem-tela-ogranichennogo-poverhnostjami