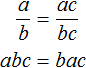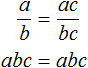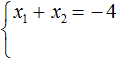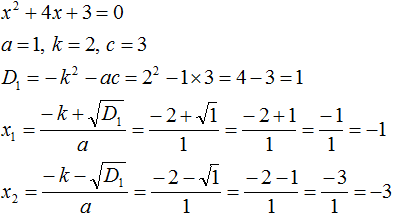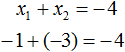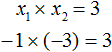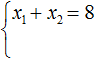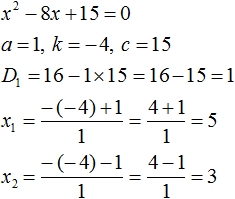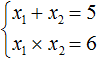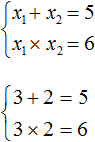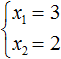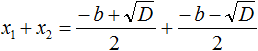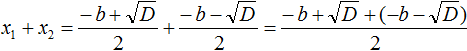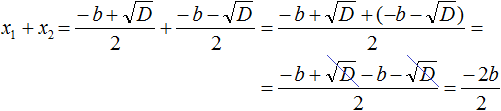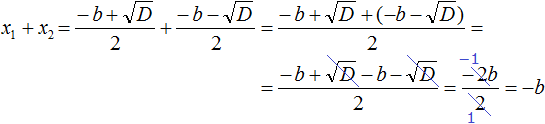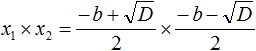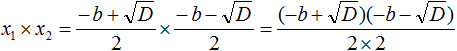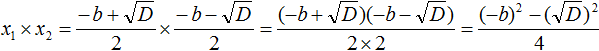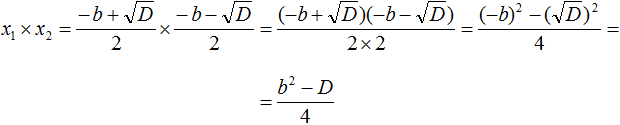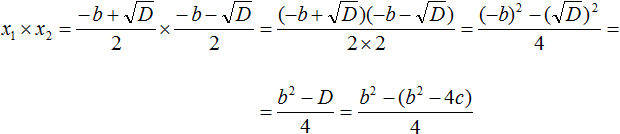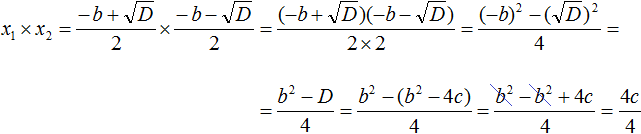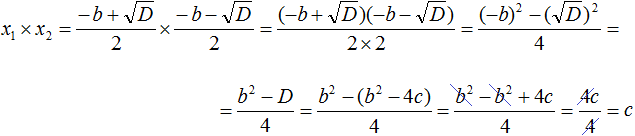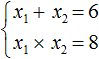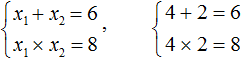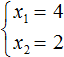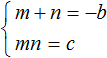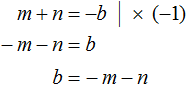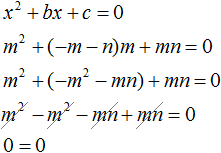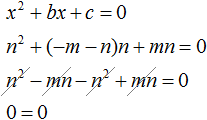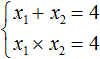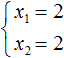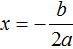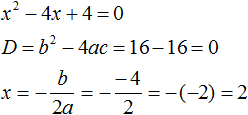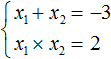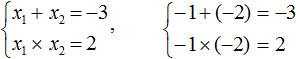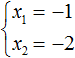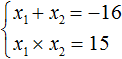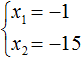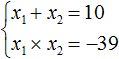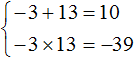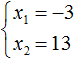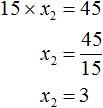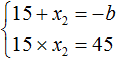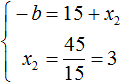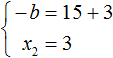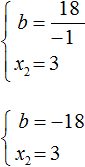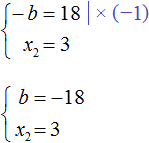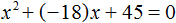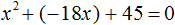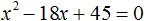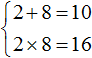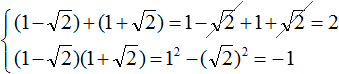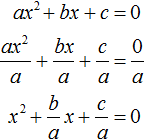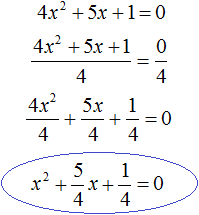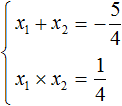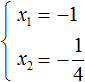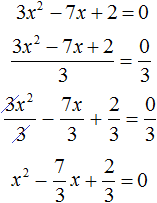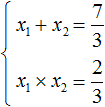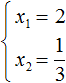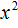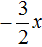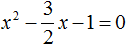Как найти сумму целых корней уравнения

Как найти сумму целых корней уравнения

Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.

Решите уравнение: `x^3 +4x^2 — 2x-3=0`.

Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:

`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`

Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.

Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.

Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что

`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.

Умножим обе части на `q^n`, получаем:

`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.

Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:

Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.

Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.

Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.

а) `x^4+4x^3-102x^2-644x-539=0`; (15)

б) `6x^4-35x^3+28x^2+51x+10=0`. (16)

а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:

Поэтому `p` может принимать значения:

Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:

Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:

1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.

2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.

б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:

Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем

Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:

Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.

К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.

Разложите на множители:

а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`

Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:

в) Вынесем `x^2` за скобки и сгруппируем:

Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:

В итоге получаем:

Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).

г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению

Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.

Прибегнем к методу неопределённых коэффициентов. Пусть

Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:

Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:

Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.

Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:

2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:

Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.

Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому

Далее каждый из квадратных трёхчленов можно разложить на множители.

Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.

Что такое сумма корней уравнения. Как найти сумму корней уравнения

Между корнями и коэффициентами квадратного уравнения , помимо формул корней, существуют другие полезные соотношения, которые задаются теоремой Виета . В этой статье мы дадим формулировку и доказательство теоремы Виета для квадратного уравнения. Дальше рассмотрим теорему, обратную теореме Виета. После этого разберем решения наиболее характерных примеров. Наконец, запишем формулы Виета, задающие связь между действительными корнями алгебраического уравнения степени n и его коэффициентами.

Навигация по странице.

Теорема Виета, формулировка, доказательство

Из формул корней квадратного уравнения a·x 2 +b·x+c=0 вида , где D=b 2 −4·a·c , вытекают соотношения x 1 +x 2 =−b/a , x 1 ·x 2 =c/a . Эти результаты утверждаются теоремой Виета :

Если x 1 и x 2 – корни квадратного уравнения a·x 2 +b·x+c=0 , то сумма корней равна отношению коэффициентов b и a , взятому с противоположным знаком, а произведение корней равно отношению коэффициентов c и a , то есть, .

Доказательство теоремы Виета проведем по следующей схеме: составим сумму и произведение корней квадратного уравнения, используя известные формулы корней, после этого преобразуем полученные выражения, и убедимся, что они равны −b/a и c/a соответственно.

Начнем с суммы корней, составляем ее . Теперь приводим дроби к общему знаменателю, имеем . В числителе полученной дроби , после чего : . Наконец, после на 2 , получаем . Этим доказано первое соотношение теоремы Виета для суммы корней квадратного уравнения. Переходим ко второму.

Составляем произведение корней квадратного уравнения: . Согласно правилу умножения дробей, последнее произведение можно записать как . Теперь выполняем умножение скобки на скобку в числителе, но быстрее свернуть это произведение по формуле разности квадратов , так . Дальше, вспомнив , выполняем следующий переход . А так как дискриминанту квадратного уравнения отвечает формула D=b 2 −4·a·c , то в последнюю дробь вместо D можно подставить b 2 −4·a·c , получаем . После раскрытия скобок и приведения подобных слагаемых приходим к дроби , а ее сокращение на 4·a дает . Этим доказано второе соотношение теоремы Виета для произведения корней.

Если опустить пояснения, то доказательство теоремы Виета примет лаконичный вид:
,
.

Остается лишь заметить, что при равном нулю дискриминанте квадратное уравнение имеет один корень. Однако, если считать, что уравнение в этом случае имеет два одинаковых корня, то равенства из теоремы Виета также имеют место. Действительно, при D=0 корень квадратного уравнения равен , тогда и , а так как D=0 , то есть, b 2 −4·a·c=0 , откуда b 2 =4·a·c , то .

На практике наиболее часто теорема Виета используется применительно к приведенному квадратному уравнению (со старшим коэффициентом a , равным 1 ) вида x 2 +p·x+q=0 . Иногда ее и формулируют для квадратных уравнений именно такого вида, что не ограничивает общности, так как любое квадратное уравнение можно заменить равносильным уравнением , выполнив деление его обеих частей на отличное от нуля число a . Приведем соответствующую формулировку теоремы Виета:

Сумма корней приведенного квадратного уравнения x 2 +p·x+q=0 равна коэффициенту при x , взятому с противоположным знаком, а произведение корней – свободному члену, то есть, x 1 +x 2 =−p , x 1 ·x 2 =q .

Теорема, обратная теореме Виета

Вторая формулировка теоремы Виета, приведенная в предыдущем пункте, указывает, что если x 1 и x 2 корни приведенного квадратного уравнения x 2 +p·x+q=0 , то справедливы соотношения x 1 +x 2 =−p , x 1 ·x 2 =q . С другой стороны, из записанных соотношений x 1 +x 2 =−p , x 1 ·x 2 =q следует, что x 1 и x 2 являются корнями квадратного уравнения x 2 +p·x+q=0 . Иными словами, справедливо утверждение, обратное теореме Виета. Сформулируем его в виде теоремы, и докажем ее.

Если числа x 1 и x 2 таковы, что x 1 +x 2 =−p и x 1 ·x 2 =q , то x 1 и x 2 являются корнями приведенного квадратного уравнения x 2 +p·x+q=0 .

После замены в уравнении x 2 +p·x+q=0 коэффициентов p и q их выражения через x 1 и x 2 , оно преобразуется в равносильное уравнение .

Подставим в полученное уравнение вместо x число x 1 , имеем равенство x 1 2 −(x 1 +x 2)·x 1 +x 1 ·x 2 =0 , которое при любых x 1 и x 2 представляет собой верное числовое равенство 0=0 , так как x 1 2 −(x 1 +x 2)·x 1 +x 1 ·x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0 . Следовательно, x 1 – корень уравнения x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0 , а значит, x 1 – корень и равносильного ему уравнения x 2 +p·x+q=0 .

Если же в уравнение x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0 подставить вместо x число x 2 , то получим равенство x 2 2 −(x 1 +x 2)·x 2 +x 1 ·x 2 =0 . Это верное равенство, так как x 2 2 −(x 1 +x 2)·x 2 +x 1 ·x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0 . Следовательно, x 2 тоже является корнем уравнения x 2 −(x 1 +x 2)·x+x 1 ·x 2 =0 , а значит, и уравнения x 2 +p·x+q=0 .

На этом завершено доказательство теоремы, обратной теореме Виета.

Примеры использования теоремы Виета

Пришло время поговорить о практическом применении теоремы Виета и обратной ей теоремы. В этом пункте мы разберем решения нескольких наиболее характерных примеров.

Начнем с применения теоремы, обратной теореме Виета. Ее удобно применять для проверки, являются ли данные два числа корнями заданного квадратного уравнения. При этом вычисляется их сумма и разность, после чего проверяется справедливость соотношений . Если выполняются оба этих соотношения, то в силу теоремы, обратной теореме Виета, делается вывод, что данные числа являются корнями уравнения. Если же хотя бы одно из соотношений не выполняется, то данные числа не являются корнями квадратного уравнения. Такой подход можно использовать при решении квадратных уравнений для проверки найденных корней.

Какая из пар чисел 1) x 1 =−5 , x 2 =3 , или 2) , или 3) является парой корней квадратного уравнения 4·x 2 −16·x+9=0 ?

Коэффициентами заданного квадратного уравнения 4·x 2 −16·x+9=0 являются a=4 , b=−16 , c=9 . Согласно теореме Виета сумма корней квадратного уравнения должна быть равна −b/a , то есть, 16/4=4 , а произведение корней должно быть равно c/a , то есть, 9/4 .

Теперь вычислим сумму и произведение чисел в каждой из трех заданных пар, и сравним их с только что полученными значениями.

В первом случае имеем x 1 +x 2 =−5+3=−2 . Полученное значение отлично от 4 , поэтому дальнейшую проверку можно не осуществлять, а по теореме, обратной теореме Виета, сразу сделать вывод, что первая пара чисел не является парой корней заданного квадратного уравнения.

Переходим ко второму случаю. Здесь , то есть, первое условие выполнено. Проверяем второе условие: , полученное значение отлично от 9/4 . Следовательно, и вторая пара чисел не является парой корней квадратного уравнения.

Остался последний случай. Здесь и . Оба условия выполнены, поэтому эти числа x 1 и x 2 являются корнями заданного квадратного уравнения.

Теорему, обратную теореме Виета, на практике можно использовать для подбора корней квадратного уравнения. Обычно подбирают целые корни приведенных квадратных уравнений с целыми коэффициентами, так как в других случаях это сделать достаточно сложно. При этом пользуются тем фактом, что если сумма двух чисел равна второму коэффициенту квадратного уравнения, взятому со знаком минус, а произведение этих чисел равно свободному члену, то эти числа являются корнями данного квадратного уравнения. Разберемся с этим на примере.

Возьмем квадратное уравнение x 2 −5·x+6=0 . Чтобы числа x 1 и x 2 были корнями этого уравнения, должны выполняться два равенства x 1 +x 2 =5 и x 1 ·x 2 =6 . Остается подобрать такие числа. В данном случае это сделать достаточно просто: такими числами являются 2 и 3 , так как 2+3=5 и 2·3=6 . Таким образом, 2 и 3 – корни данного квадратного уравнения.

Теорему, обратную теореме Виета, особенно удобно применять для нахождения второго корня приведенного квадратного уравнения, когда уже известен или очевиден один из корней. В этом случае второй корень находится из любого из соотношений .

Для примера возьмем квадратное уравнение 512·x 2 −509·x−3=0 . Здесь легко заметить, что единица является корнем уравнения, так как сумма коэффициентов этого квадратного уравнения равна нулю. Итак, x 1 =1 . Второй корень x 2 можно найти, например, из соотношения x 1 ·x 2 =c/a . Имеем 1·x 2 =−3/512 , откуда x 2 =−3/512 . Так мы определили оба корня квадратного уравнения: 1 и −3/512 .

Понятно, что подбор корней целесообразен лишь в самых простых случаях. В остальных случаях для поиска корней можно применить формулы корней квадратного уравнения через дискриминант.

Еще одно практическое применение теоремы, обратной теореме Виета, состоит в составлении квадратных уравнений по заданным корням x 1 и x 2 . Для этого достаточно вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.

Напишите квадратное уравнение, корнями которого являются числа −11 и 23 .

Обозначим x 1 =−11 и x 2 =23 . Вычисляем сумму и произведение данных чисел: x 1 +x 2 =12 и x 1 ·x 2 =−253 . Следовательно, указанные числа являются корнями приведенного квадратного уравнения со вторым коэффициентом −12 и свободным членом −253 . То есть, x 2 −12·x−253=0 – искомое уравнение.

Теорема Виета очень часто используется при решении заданий, связанных со знаками корней квадратных уравнений. Как же связана теорема Виета со знаками корней приведенного квадратного уравнения x 2 +p·x+q=0 ? Приведем два соответствующих утверждения:

• Если свободный член q – положительное число и если квадратное уравнение имеет действительные корни, то либо они оба положительные, либо оба отрицательные.
• Если же свободный член q – отрицательное число и если квадратное уравнение имеет действительные корни, то их знаки различны, другими словами, один корень положительный, а другой — отрицательный.

Эти утверждения вытекают из формулы x 1 ·x 2 =q , а также правил умножения положительных, отрицательных чисел и чисел с разными знаками. Рассмотрим примеры их применения.

R он положителен. По формуле дискриминанта находим D=(r+2) 2 −4·1·(r−1)= r 2 +4·r+4−4·r+4=r 2 +8 , значение выражения r 2 +8 положительно при любых действительных r , таким образом, D>0 при любых действительных r . Следовательно, исходное квадратное уравнение имеет два корня при любых действительных значениях параметра r .

Теперь выясним, когда корни имеют разные знаки. Если знаки корней различны, то их произведение отрицательно, а по теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену. Следовательно, нас интересуют те значения r , при которых свободный член r−1 отрицателен. Таким образом, чтобы найти интересующие нас значения r , надо решить линейное неравенство r−1 Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.

Определение суммы корней уравнения — один из нужных шагов при решении квадратных уравнений (уравнений вида ax² + bx + c = 0, где показатели a, b и c — произвольные числа, причем a ? 0) с поддержкой теоремы Виета.

Инструкция

1. Запишите квадратное уравнение в виде ax² + bx + c = 0Пример:Начальное уравнение: 12 + x²= 8xПравильно записанное уравнение: x² — 8x + 12 = 0

2. Примените теорему Виета, согласно которой, сумма корней уравнения будет равна числу «b», взятому с обратным знаком, а их произведение — числу «c».Пример:В рассматриваемом уравнении b=-8, c=12, соответственно:x1+x2=8×1∗x2=12

3. Узнайте, правильными либо негативными числами являются корни уравнений. Если и произведение и сумма корней — позитивные числа, весь из корней — правильное число. Если произведение корней — правильное, а сумма корней – негативное число, то оба корня – негативные. Если произведение корней – негативное, то корни один корень имеет знак «+», а иной знак «-» В таком случае нужно воспользоваться дополнительным правилом: «Если сумма корней – позитивное число, больший по модулю корень тоже позитивный, а если сумма корней — негативное число — больший по модулю корень — негативный».Пример:В рассматриваемом уравнении и сумма, и произведение — правильные числа: 8 и 12, значит оба корня — позитивные числа.

4. Решите полученную систему уравнений путем подбора корней. Комфортней будет начать подбор с множителей, а после этого, для проверки, подставить всякую пару множителей во второе уравнение и проверить, соответствует ли сумма данных корней решению.Пример:x1∗x2=12 Подходящими парами корней будут соответственно: 12 и 1, 6 и 2, 4 и 3Проверьте полученные пары с поддержкой уравнения x1+x2=8. Пары 12 + 1 ≠ 86 + 2 = 84 + 3 ≠ 8Соответственно корнями уравнения являются числа 6 и 8.

Уравнением называют равенство вида f(x,y,…)=g(x,y. ), где f и g функции одной либо нескольких переменных. Обнаружить корень уравнения — значит обнаружить такой комплект доводов, при котором это равенство выполняется.

• Знания по математическому обзору.

Инструкция

1. Возможен, у вас имеется уравнение вида: x+2=x/5. Для начала перенесём все компоненты этого равенства из правой части в левую, поменяв при этом знак у компонента на противоположный. В правой части этого уравнения останется нуль, то есть, получим следующее: x+2-x/5 = 0.

2. Приведём сходственные слагаемые. Получим следующее: 4х/5 + 2 = 0.

3. Дальше из полученного приведённого уравнения найдём неведомое слагаемое, в данном случае это х. Полученное значение неведомой переменной и будет решением начального уравнения. В данном случае получим следующее: x = -2,5.

Обратите внимание!
В итоге решения могу возникать лишние корни. Они не будут являться решением начального уравнения, даже если вы всё положительно решили. Непременно проверяйте все полученные решения.

Полезный совет
Полученные значения незнакомой неизменно проверяйте. Это дозволено примитивно сделать, подставив полученное значение в начальное уравнение. Если равенство правильно, то решение верное.

Теорема Виета устанавливает прямую связь между корнями (х1 и х2) и показателями (b и c, d) уравнения типа bx2+cx+d=0. C подмогой этой теоремы дозволено, не определяя значения корней, посчитать их сумму, дерзко говоря, в уме. В этом нет ничего трудного, основное — знать некоторые правила.

Инструкция

1. Приведите к стандартному виду исследуемое квадратное уравнение, дабы все показатели степени шли по порядку убывания, то есть вначале наивысшая степень – х2, а в конце нулевая степень – х0. Уравнение примет вид: b*x2 + c*x1 + d*х0 = b*x2 + c*x + d = 0.

2. Проверьте неотрицательность дискриминанта. Это проверка нужна для того, дабы удостовериться, что корни у уравнения есть. D (дискриминант) принимает вид:D = c2 – 4*b*d. Тут есть несколько вариантов. D – дискриминант – правильный, что обозначает, что у уравнения есть два корня. D – равен нулю, из этого следует, что корень есть, но он двойственный, то есть х1=х2. D – негативный, для курса школьной алгебры это условие обозначает, что корней нет, для высшей математики – корни есть, но они комплексные.

3. Определите сумму корней уравнения. При помощи теоремы Виета это сделать легко: b*x2+c*x+d = 0. Сумма корней уравнения прямо пропорциональна «–c» и обратно пропорциональна показателю «b». А именно, x1+x2 = -c/b. Определите произведение корней по формулировке – произведение корней уравнения прямо пропорционально «d» и обратно пропорционально показателю «b»: х1*х2 = d/b.

Обратите внимание!
Если вы получили негативный дискриминант, это не значит, что корней нет. Это значит, что корнями уравнения являются так называемые комплексные корни. Теорема Виета применима и в этом случае, но ее вид будет немножко изменен: [-c+(-i)*(-c2 + 4*b*d)0.5]/ = x1,2

Полезный совет
Если вы столкнулись не с квадратным уравнением, а с кубическим либо уравнением степени n: b0*xn + b1*xn-1 +…..+ bn = 0, то для вычисления суммы либо произведения корней уравнения вы верно так же можете воспользоваться теоремой Виета:1. –b1/b0 = x1 + x2 + x3 +….+ xn,2. b2/b0 = x1*x2+….+xn-1*xn,3. (-1)n * (bn/b0) = x1*x2*x3*….*xn.

Если при подстановке числа в уравнение получается правильное равенство, такое число называют корнем. Корни могут быть правильными, негативными и нулевыми. Среди каждого множества корней уравнения выделяют максимальные и минимальные.

Инструкция

1. Обнаружьте все корни уравнения, среди них выберите негативный, если таковой имеется. Пускай, скажем, дано квадратное уравнение 2x?-3x+1=0. Примените формулу поиска корней квадратного уравнения: x(1,2)=/2=/2=/2, тогда x1=2, x2=1. Несложно подметить, что негативных среди них нет.

2. Обнаружить корни квадратного уравнения дозволено также при помощи теоремы Виета. Согласно этой теореме x1+x1=-b, x1?x2=c, где b и c – соответственно показатели уравнения x?+bx+c=0. Применяя эту теорему, дозволено не вычислять дискриминант b?-4ac, что в некоторых случаях может значительно упростить задачу.

3. Если в квадратном уравнении показатель при x четный, дозволено использовать не основную, а сокращенную формулу для поиска корней. Если основная формула выглядит как x(1,2)=[-b±?(b?-4ac)]/2a, то в сокращенном виде она записывается так: x(1,2)=[-b/2±?(b?/4-ac)]/a. Если в квадратном уравнении нет свободного члена, довольно легко перенести x за скобки. А изредка левая часть складывается в полный квадрат: x?+2x+1=(x+1)?.

4. Существуют виды уравнений, которые дают не одно число, а целое уйма решений. Скажем, тригонометрические уравнения. Так, результатом к уравнению 2sin?(2x)+5sin(2x)-3=0 будет x=?/4+?k, где k – целое число. То есть, при подстановке всякого целого значения параметра k довод x будет удовлетворять заданному уравнению.

5. В тригонометрических задачах может понадобиться обнаружить все негативные корни либо наивысший из негативных. В решении таких задач используются логические рассуждения либо способ математической индукции. Подставьте несколько целых значений для k в выражение x=?/4+?k и пронаблюдайте, как ведет себя довод. К слову, наибольшим негативным корнем в предыдущем уравнении будет x=-3?/4 при k=1.

Обратите внимание!
В данном примере был рассмотрен вариант квадратного уравнения, в котором a=1. Для того дабы тем же методом решить полное квадратное уравнение, где a&ne 1, нужно составить вспомогательное уравнение, приведя «a» к единице.

Полезный совет
Используйте данный метод решения уравнений для того, дабы стремительно обнаружить корни. Также он поможет в случае, если вам нужно решить уравнение в уме, не прибегая к записям.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену.

(Напомним: приведенное квадратное уравнение – это уравнение, где первый коэффициент равен 1).

Пусть квадратное уравнение ax 2 + bx + c = 0 имеет корни х 1 и х 2 . Тогда по теореме Виета:

Приведенное уравнение x 2 – 7x + 10 = 0 имеет корни 2 и 5.

Сумма корней равна 7, а произведение равно 10.

А в нашем уравнении второй коэффициент равен -7, а свободный член 10.

Таким образом, сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней – свободному члену.

Довольно часто встречаются квадратные уравнения, которые можно легко вычислить с помощью теоремы Виета – больше того, с ее помощью их вычислять проще. В этом легко убедиться как на предыдущем примере, так и на следующем.

Пример 2 . Решить квадратное уравнение х 2 – 2х – 24 = 0.

Применяем теорему Виета и записываем два тождества:

Подбираем такие множители для –24, чтобы их сумма была равна 2. После недолгих размышлений находим: 6 и –4. Проверим:

Как вы заметили, на практике суть теоремы Виета заключается в том, чтобы в приведенном квадратном уравнении свободный член разложить на такие множители, сумма которых равна второму коэффициенту с противопложным знаком. Эти множители и будут корнями.

Значит, корнями нашего квадратного уравнения являются 6 и –4.

Ответ: х 1 = 6, х 2 = –4.

Пример 3 . Решим квадратное уравнение 3х 2 + 2х – 5 = 0.

Здесь мы имеем дело не с приведенным квадратным уравнением. Но и такие уравнения тоже можно решать с помощью теоремы Виета, если их коэффициенты уравновешены – например, если сумма первого и третьего коэффициентов равна второму с обратным знаком.

Коэффициенты уравнения уравновешены: сумма первого и третьего членов равны второму с противоположным знаком:

В соответствии с теоремой Виета

х 1 + х 2 = –2/3
х 1 · х 2 = –5/3.

Нам надо найти такие два числа, сумма которых равна –2/3, а произведение –5/3. Эти числа и будут корнями уравнения.

Первое число угадывается сразу: это 1. Ведь при х = 1 уравнение превращается в простейшее сложение-вычитание:
3 + 2 – 5 = 0. Как найти второй корень?
Представим 1 в виде 3/3, чтобы все числа имели одинаковый знаменатель: так проще. И сразу напрашиваются дальнейшие действия. Если х 1 = 3/3, то:

Решаем простое уравнение:

Ответ: х 1 = 1; х 2 = –5/3

Пример 4 : Решить квадратное уравнение 7x 2 – 6x – 1 = 0.

Один корень обнаруживается сразу – он прямо в глаза бросается: х 1 = 1 (потому что получается простая арифметика: 7 – 6 – 1 = 0).

Коэффициенты уравнения уравновешены: сумма первого и третьего равны второму с обратным знаком:
7 + (– 1) = 6.

В соответствии с теоремой Виета составляем два тождества (хотя в данном случае достаточно одного из них):

Подставляем значение х 1 в любое из этих двух выражений и находим х 2:

Ответ : х 1 = 1; х 2 = –1/7

Дискриминант приведенного квадратного уравнения.

Дискриминант приведенного квадратного уравнения можно вычислять как общей формуле, так и по упрощенной:

При D = 0 корни приведенного уравнения можно вычислять по формуле:

Теорема Виета

Что называют теоремой?

Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.

Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.

Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.

Например, теоремой можно назвать следующее утверждение:

«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».

А затем привести такое доказательство:

Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с . Тогда полýчится дробь . Докáжем, что дроби и равны. То есть докажем, что равенство является верным.

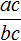
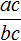
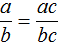
Для доказательства этого равенства воспользуемся основным свойством пропорции:

От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:

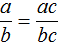
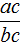
Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.

Теорема Виета

Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:

Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.

То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x₁ и x₂ , то справедливы следующие два равенства:

Знак системы (фигурная скобка) говорит о том, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .

Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:

А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:

Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:

Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x₁ + x₂ к этому коэффициенту, то получается верное равенство:

А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:

Значит выражение 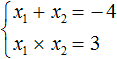является справедливым.

Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:

А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:

Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:

Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.

А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .

Значит выражение 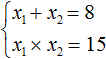является справедливым.

Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.

Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:

Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:

А значит записывать выражение 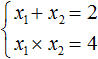не имеет смысла.

Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.

Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x₁ × x₂ = 6 будет выполняться только в двух случаях: если значения x₁ и x₂ положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x₁ + x₂ = 5 , поскольку его правая часть равна положительному числу. А значения x₁ и x₂ должны удовлетворять как равенству x₁ + x₂ = 5 , так и равенству x₁ × x₂ = 6.

Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x₁ + x₂ = 5 так и равенству x₁ × x₂ = 6 . Очевидно, что таковыми являются корни 3 и 2

Доказательство теоремы Виета

Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Вспомним формулы корней квадратного уравнения:

Найдём сумму корней x₁ и x₂ . Для этого подставим в выражение x₁ + x₂ вместо x₁ и x₂ соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2

Запишем правую часть в виде дроби с одним знаменателем:

Раскроем скобки в числителе и приведём подобные члены:

Сократим дробь 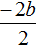на 2 , тогда получим −b

Теперь аналогично докажем, что произведение x₁ × x₂ равно свободному члену c .

Подставим вместо x₁ и x₂ соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:

Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:

В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится 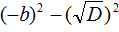А знаменатель будет равен 4

Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение 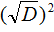станет равно просто D

Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c

В получившемся выражении раскроем скобки в числителе и приведём подобные члены:

Сократим получившуюся дробь на 4

Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x₁ + x₂ = −b ), а произведение корней равно свободному члену ( x₁ × x₂ = c ). Теорема доказана.

Теорема, обратная теореме Виета

Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x₁ и x₂ равно свободному члену уравнения x 2 + bx + c = 0, то числа x₁ и x₂ являются корнями уравнения x 2 + bx + c = 0.

Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.

Так, доказывая теорему Виета мы пришли к заключению, что сумма x₁ и x₂ равна −b , а произведение x₁ и x₂ равно c . В обратной же теореме это заключение служит утверждением.

Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:

А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .

Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.

В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.

Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8

Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x₁ + x₂ = 6 , так и равенству x₁ × x₂ = 8

Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x₁ × x₂ = 8 нужно найти такие x₁ и x₂ , произведение которых равно 8.

Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.

4 × 2 = 8
1 × 8 = 8

Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли не только равенству x₁ × x₂ = 8 , но и равенству x₁ + x₂ = 6 .

Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x₁ × x₂ = 8 , но не удовлетворяют равенству x₁ + x₂ = 6 .

Зато значения 4 и 2 подходят как равенству x₁ × x₂ = 8 , так и равенству x₁ + x₂ = 6 , поскольку эти значения удовлетворяют обоим равенствам:

Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .

Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x₁ и x₂ обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:

Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0

Для начала запишем, что сумма m и n равна −b , а произведение mn равно c

Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .

Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1

Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b

Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .

Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .

Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.

Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .

Примеры решения уравнений по теореме, обратной теореме Виета

Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.

Запишем сумму корней x₁ и x₂ и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x₁ и x₂ и приравняем его к свободному члену :

В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4

Значение x₁ совпадает с x₂ . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле

Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x₁ и x₂ совпадают.

Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Теперь подберём значения x₁ и x₂ . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x₁ + x₂ равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.

Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.

Если подберём корни с разными знаками, то не будет выполняться равенство x₁ × x₂ = 2 .

Если подберем положительные корни, то будет выполняться равенство x₁ × x₂ = 2 , но не будет выполняться равенство x₁ + x₂ = −3 .

Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.

Тогда равенствам будут удовлетворять числа −1 и −2 .

Итак, корнями являются числа −1 и −2

Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.

Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.

Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15

Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.

Запишем сумму и произведение корней данного уравнения:

Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10

Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13

Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .

По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45

При этом один из корней уже известен — это корень 15 .

Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3

Этот второй корень также можно было бы получить, выразив из равенства 15 × x₂ = 45 переменную x₂

Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:

По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:

Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:

Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45

Из этой системы следует найти x₂ и b . Выразим эти параметры:

Из этой системы мы видим, что x₂ равно 3. Подставим его в первое равенство:

Теперь из первого равенства мы видим, что −b равно 18

Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18

Этот же результат можно получить если в выражении 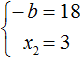умножить первое равенство на −1

Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b

Выполним умножение −18 на x . Получим −18x

Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .

В этом задании корни уже известны. То есть x₁ = 2 , x₂ = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .

Запишем сумму и произведение корней:

По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .

Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .

Значит b = −10 , c = 16 . Отсюда:

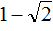
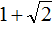
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа и .

Запишем сумму и произведение корней:

Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:

Когда квадратное уравнение неприведённое

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.

Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .

Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a

Получилось уравнение 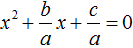, которое является приведённым. В нём второй коэффициент равен , а свободный член равен . Тогда сумма и произведение корней будут выглядеть так:

Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4

Получили приведённое квадратное уравнение. В нём второй коэффициент равен , а свободный член . Тогда по теореме Виета имеем:

Отсюда методом подбора находим корни −1 и

Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.

Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0

Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.

Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2

Получили уравнение 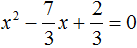. Запишем сумму и произведение корней этого уравнения:

Отсюда методом подбора находим корни 2 и

Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0

Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2

Далее если −3x разделить на 2 , то полýчится 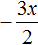. Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде

Далее если −2 разделить на 2 , то полýчится −1

Прирáвниваем получившееся выражение к нулю:

Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:

Отсюда методом подбора находим корни 2 и