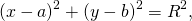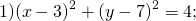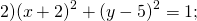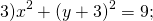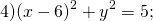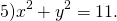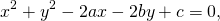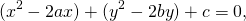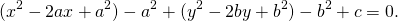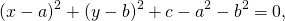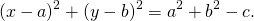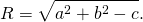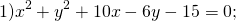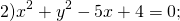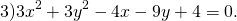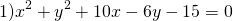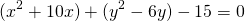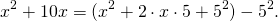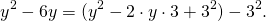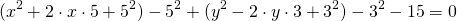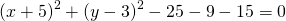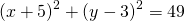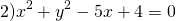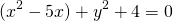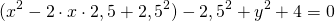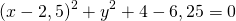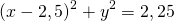Как найти точку на окружности по уравнению

Как найти точки на окружности заданной уравнением

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Как найти координаты окружности по уравнению

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут — Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

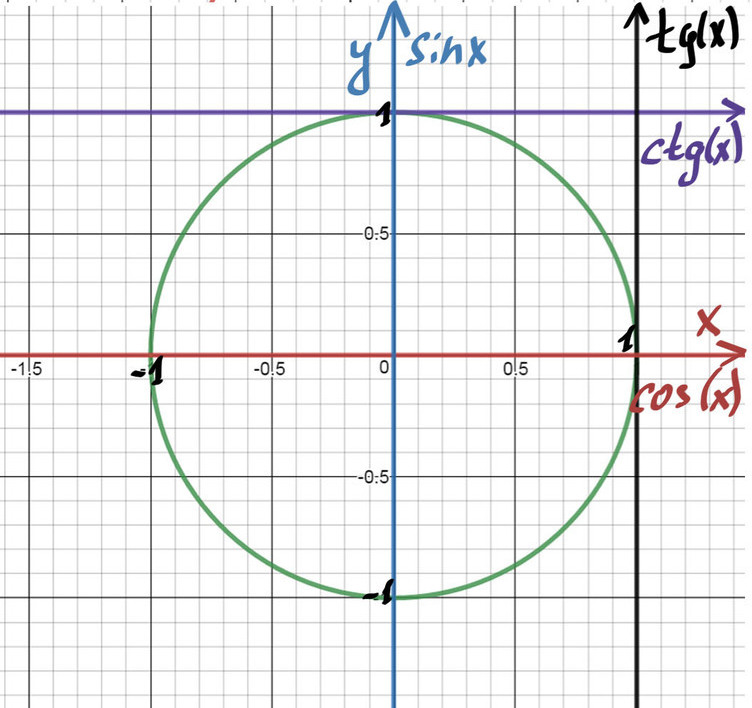
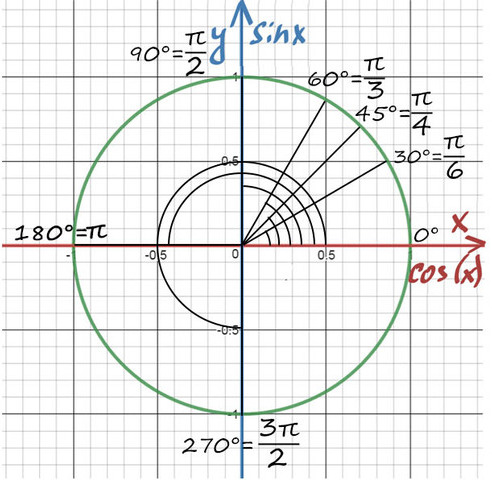
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

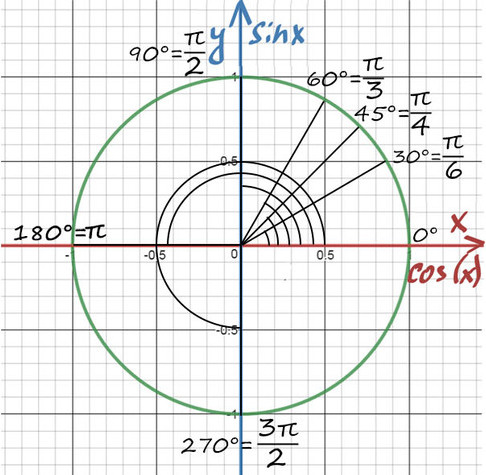
А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

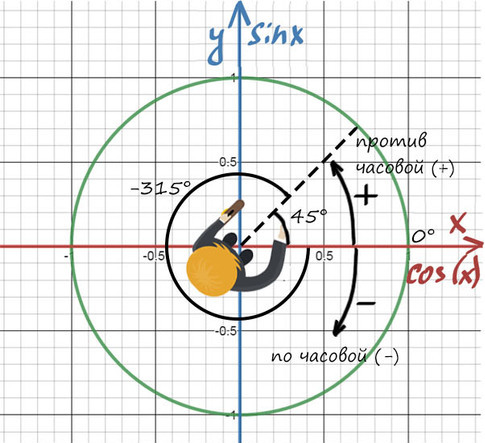
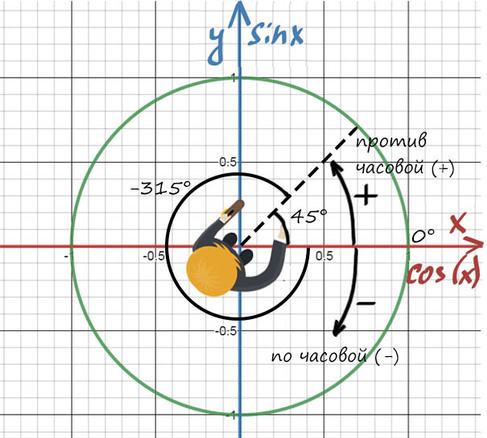
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

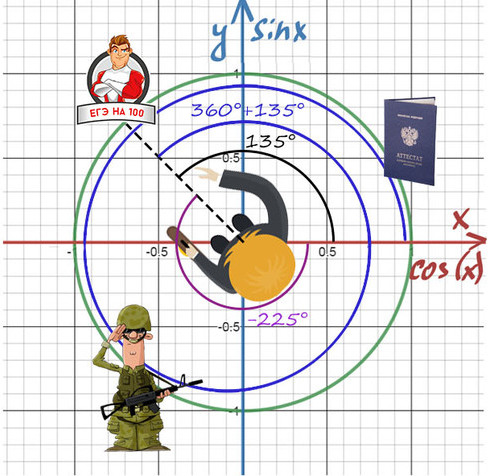
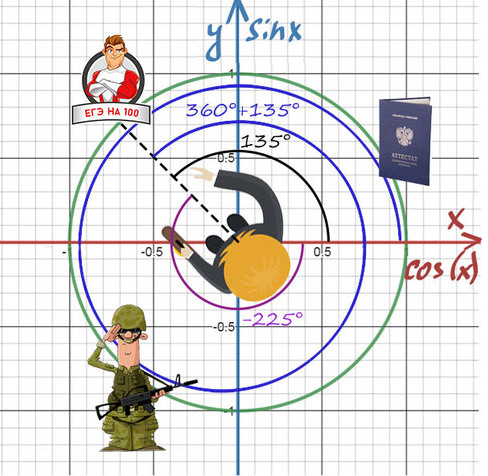
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

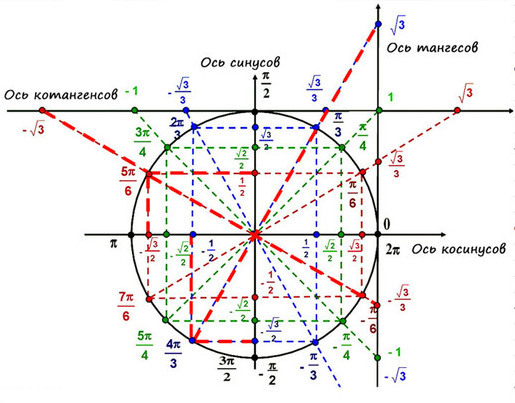
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

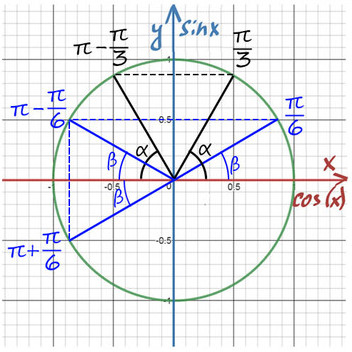
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

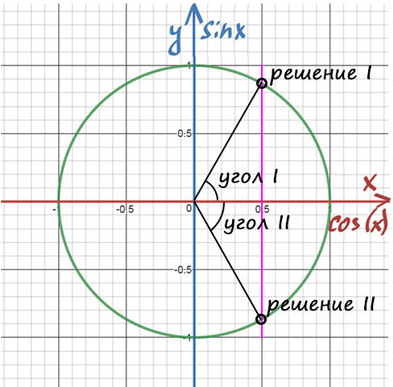
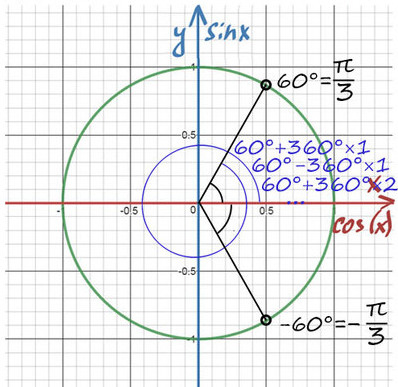
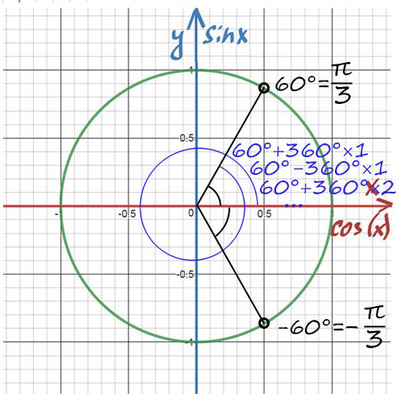
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

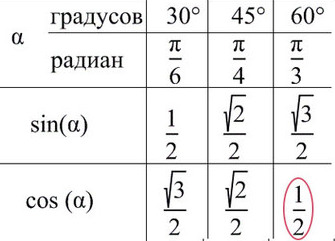
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

Или запомнить такой прием:

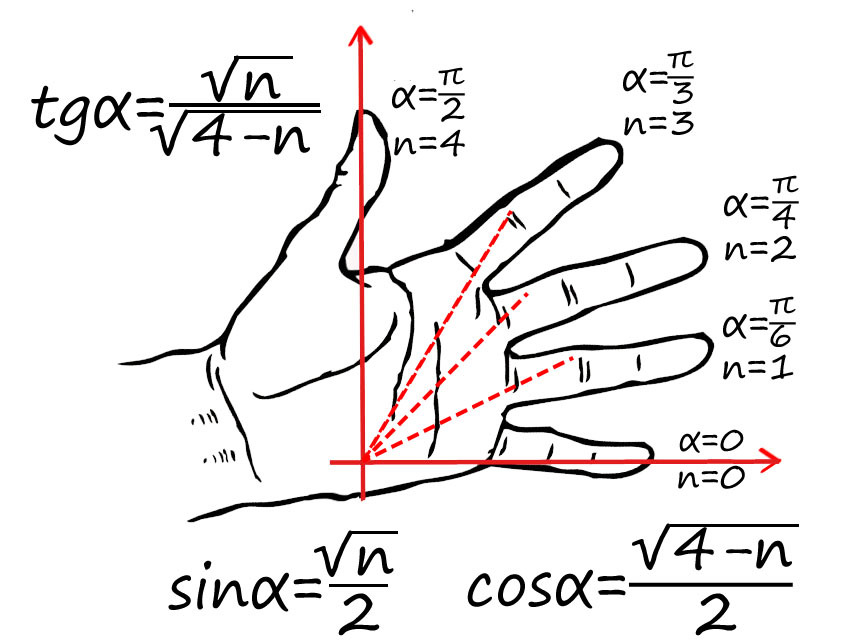
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

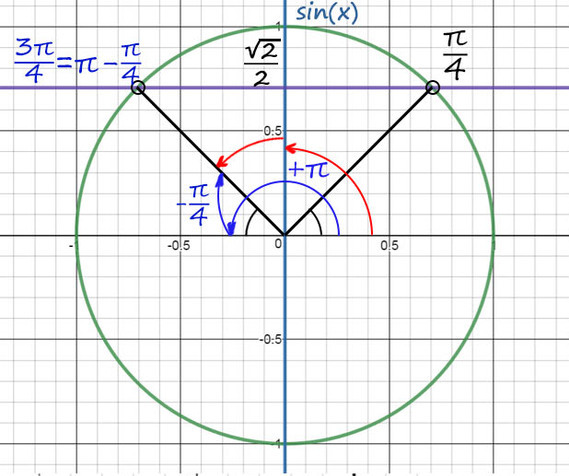
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

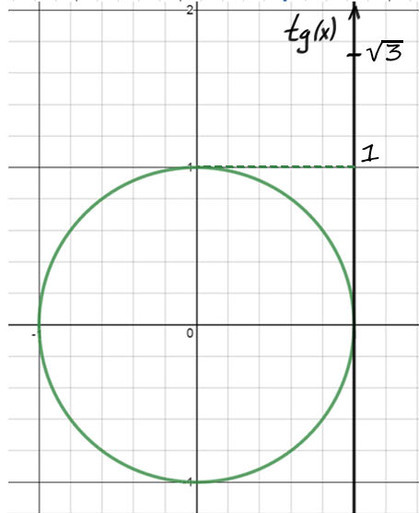
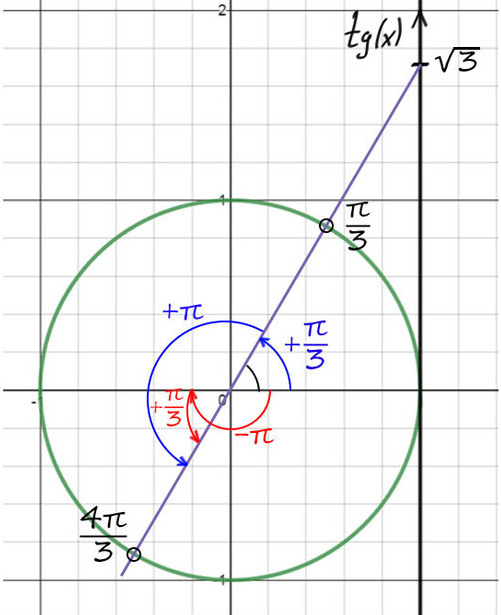
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

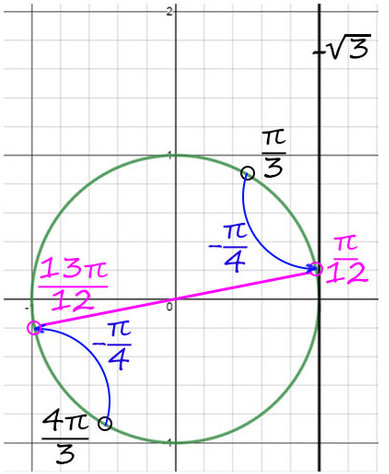
4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

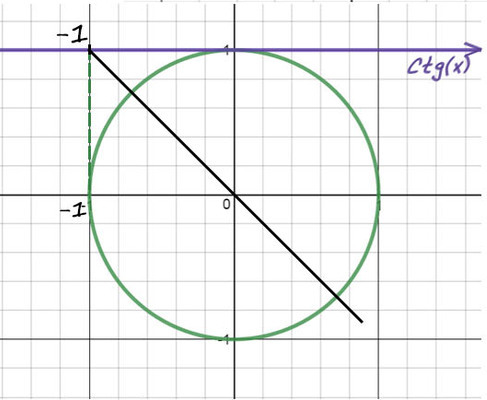
Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

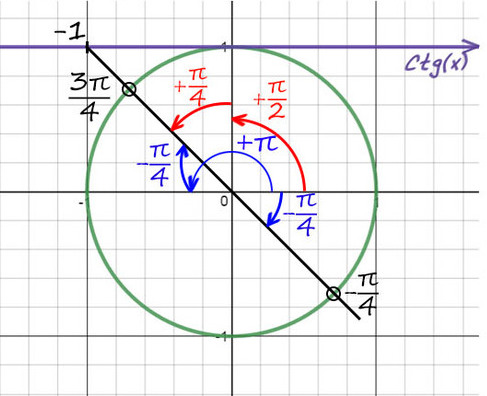
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
Точки пересечения с окружностью и будут являться корнями уравнения.
Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

Уравнение окружности.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

источники:

http://www.profmeter.com.ua/communication/learning/course/course7/chapter0552/?LESSON_PATH=456.552

http://planetcalc.ru/9507/