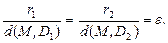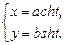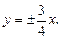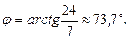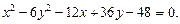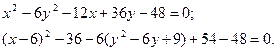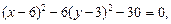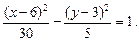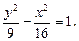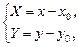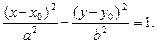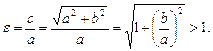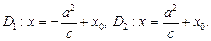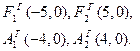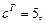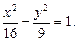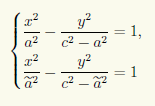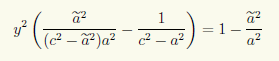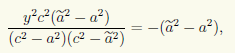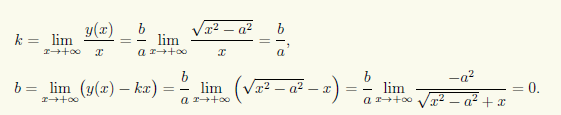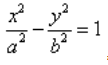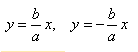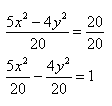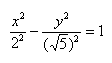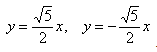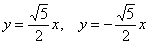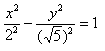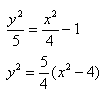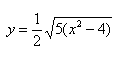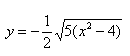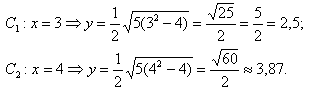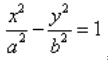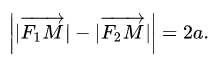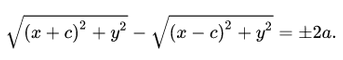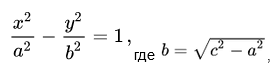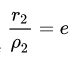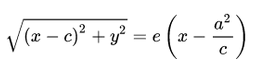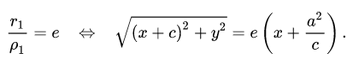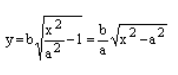Гипербола: формулы, примеры решения задач
Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Как найти центр гиперболы по уравнению
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac ), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac ) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac -1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color >) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: База знаний, Уроки Tag: Гипербола Leave a comment
Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
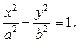
где 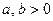
Параметры гиперболы:
Точки F1(–c, 0), F2(c, 0), где 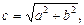
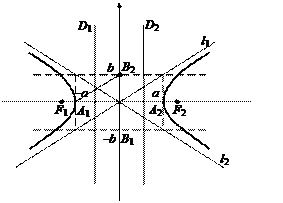 |
Величина 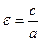
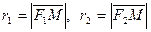
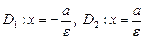
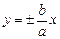
Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством
Говорят, что уравнение
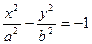
задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде
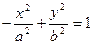
В таком случае ось 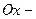
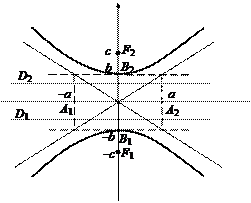 |
Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).
Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:
Пример 1. Привести уравнение гиперболы
к каноническому виду, найти еепараметры, изобразить гиперболу.
Решение. Разделим левую и правую части заданного уравнения на 144: 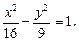
Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А1А2 = 2а = 8 и В1В2 = 2b = 6 соответственно. Через полученные точки А1(–4, 0), А2(4, 0), В1(0, –3), В2(0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу
 |
Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой


откуда получаем
Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой
Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:
которое делением на 30 приводится к виду
Это уравнение гиперболы, центр которой лежит в точке 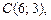
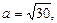
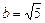
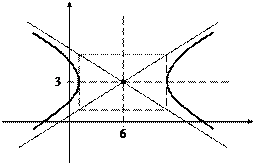 |
Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы 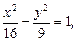
Решение.Уравнение гиперболы, сопряженной данной, –
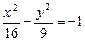
Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния 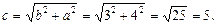
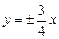
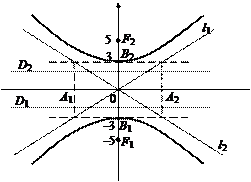 |
Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.
Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.
Решение. Искомое уравнение можно рассматривать как уравнение гиперболы 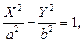
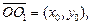
получим уравнение гиперболы
Определим параметры. Центр гиперболы определяет точка O¢(x0; y0), а значит, действительная ось задается уравнением x = x0,а мнимая – уравнением y = y0. Ее вершинами являются точки 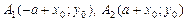
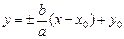
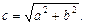
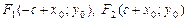
Директрисы D1 и D2 задаются уравнениями
Пример 5.Написать уравнение гиперболы, имеющей вершины в фокусах эллипса 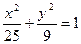
Решение.Уравнение 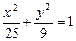
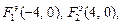
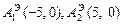
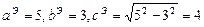
Тогда для искомой гиперболы известно, что
Значит, основные параметры гиперболы есть:
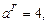
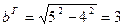
Используя данную информацию, приходим к уравнению гиперболы
Задания для самостоятельного решения
Дата добавления: 2014-12-16 ; Просмотров: 6979 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Определение 7.2. Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой.
Замечание 7.2. Говоря о разности расстояний, подразумевают, что из большего расстояния вычитается меньшее. Это значит, что на самом деле для гиперболы постоянным является модуль разности расстояний от любой ее точки до двух фиксированных точек. #
Определение гиперболы аналогично определению эллипса. Различие между ними лишь в том, что для гиперболы постоянна разность расстояний до фиксированных точек, а для эллипса — сумма тех же расстояний. Поэтому естественно, что у этих кривых много общего как в свойствах, так и в используемой терминологии.
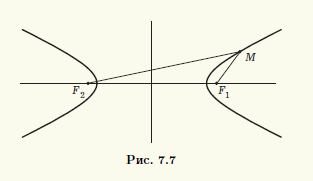
Фиксированные точки в определении гиперболы (обозначим их F1 и F2) называют фокусами гиперболы. Расстояние между ними (обозначим его 2с) называют фокальным расстоянием, а отрезки F1M и F2M, соединяющие произвольную точку M на гиперболе с ее фокусами, — фокальными радиусами.
Вид гиперболы полностью определяется фокальным расстоянием |F1F2| = 2с и значением постоянной величины 2а, равной разности фокальных радиусов, а ее положение на плоскости — положением фокусов F1 и F2.
Из определения гиперболы следует, что она, как и эллипс, симметрична относительно прямой, проходящей через фокусы, а также относительно прямой, которая делит отрезок F1F2 пополам и перпендикулярна ему (рис. 7.7). Первую из этих осей симметрии называют действительной осью гиперболы, а вторую — ее мнимой осью. Постоянную величину а, участвующую в определении гиперболы, называют действительной полуосью гиперболы.
Середина отрезка F1F2, соединяющего фокусы гиперболы, лежит на пересечении ее осей симметрии и поэтому является центром симметрии гиперболы, который называют просто центром гиперболы.
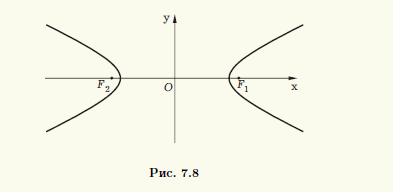
Для гиперболы действительная ось 2а должна быть не больше, чем фокальное расстояние 2с, так как для треугольника F1MF2 (см. рис. 7.7) справедливо неравенство ||F1M| — |F2M| | ≤ |F1F2|. Равенство а = с выполнено только для тех точек M, которые лежат на действительной оси симметрии гиперболы вне интервала F1F2. Отбрасывая этот вырожденный случай, далее будем предполагать, что а 2а. Согласно замечанию 7.2, гипербола состоит из тех точек M(х; у), для которых | |F1M| — — |F2M| | = 2а. Выберем прямоугольную систему координат Oxy так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс (рис. 7.8). Такую систему координат для рассматриваемой гиперболы называют канонической, а соответствующие переменные — каноническими.
В канонической системе координат фокусы гиперболы имеют координаты F1(c; 0) и F2(—с; 0). Используя формулу расстояния между двумя точками, запишем условие ||F1M| — |F2M|| = 2а в координатах |√((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 )| = 2а, где (x; у) — координаты точки M. Чтобы упростить это уравнение, избавимся от знака модуля: √((х — с) 2 + у 2 ) — √((х + с) 2 + у 2 ) = ±2а, перенесем второй радикал в правую часть и возведем в квадрат: (х — с) 2 + у 2 = (х + с) 2 + у 2 ± 4а √((х + с) 2 + у 2 ) + 4а 2 . После упрощения получим —εх — а = ±√((х + с) 2 + у 2 ), или
√((х + с) 2 + у 2 ) = |εх + а| (7.7)
где ε = с/а. Возведем в квадрат вторично и снова приведем подобные члены: (ε 2 — 1)х 2 — у 2 = с 2 — а 2 , или, учитывая равенство ε = с/а и полагая b 2 = c 2 — a 2 ,
x 2 /a 2 — y 2 /b 2 = 1 (7.8)
Величину b > 0 называют мнимой полуосью гиперболы.
Итак, мы установили, что любая точка на гиперболе с фокусами F1(с;0) и F2(—с; 0) и действительной полуосью а удовлетворяет уравнению (7.8). Но надо также показать, что координаты точек вне гиперболы этому уравнению не удовлетворяют. Для этого мы рассмотрим семейство всех гипербол с данными фокусами F1 и F2. У этого семейства гипербол оси симметрии являются общими. Из геометрических соображений ясно, что каждая точка плоскости (кроме точек, лежащих на действительной оси симметрии вне интервала F1F2, и точек, лежащих на мнимой оси симметрии) принадлежит некоторой гиперболе семейства, причем только одной, так как разность расстояний от точки до фокусов F1 и F2 меняется от гиперболы к гиперболе. Пусть координаты точки M(х; у) удовлетворяют уравнению (7.8), а сама точка принадлежит гиперболе семейства с некоторым значением ã действительной полуоси. Тогда, как мы доказали, ее координаты удовлетворяют уравнению 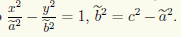
имеет хотя бы одно решение. Непосредственной проверкой убеждаемся, что при ã ≠ а это невозможно. Действительно, исключив, например, x из первого уравнения:
после преобразований получаем уравнение
которое при ã ≠ а не имеет решений, так как 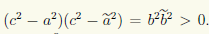
Вид гиперболы. По своему виду гипербола (7.8) заметно отличается от эллипса. Учитывая наличие двух осей симметрии у гиперболы, достаточно построить ту ее часть, которая находится в первой четверти канонической системы координат. В первой четверти, т.е. при x ≥ 0, у ≥ 0, каноническое уравнение гиперболы однозначно разрешается относительно у:
у = b/a √(x 2 — а 2 ). (7.9)
Исследование этой функции y(x) дает следующие результаты.
Область определения функции — ив этой области определения она непрерывна как сложная функция, причем в точке x = а она непрерывна справа. Единственным нулем функции является точка x = а.
Найдем производную функции y(x): y'(x) = bx/a√(x 2 — а 2 ). Отсюда заключаем, что при x > а функция монотонно возрастает. Кроме того, 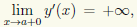
Указанная функция имеет наклонную асимптоту, это вытекает из существования двух пределов:
Наклонная асимптота описывается уравнением y = (b/a)x.
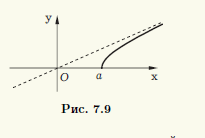
Проведенное исследование функции (7.9) позволяет построить ее график (рис. 7.9), который совпадает с частью гиперболы (7.8), содержащейся в первой четверти.
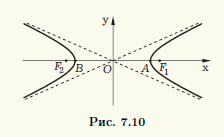
Так как гипербола симметрична относительно своих осей, вся кривая имеет вид, изображенный на рис. 7.10. Гипербола состоит из двух симметричных ветвей, расположенных по разные
стороны от ее мнимой оси симметрии. Эти ветви не ограничены с обеих сторон, причем прямые у = ±(b/a)x являются одновременно асимптотами и правой и левой ветвей гиперболы.
Оси симметрии гиперболы различаются тем, что действительная пересекает гиперболу, а мнимая, будучи геометрическим местом точек, равноудаленных от фокусов, — не пересекает (поэтому ее и называют мнимой). Две точки пересечения действительной оси симметрии с гиперболой называют вершинами гиперболы (точки A(a; 0) и B(—a; 0) на рис. 7.10).
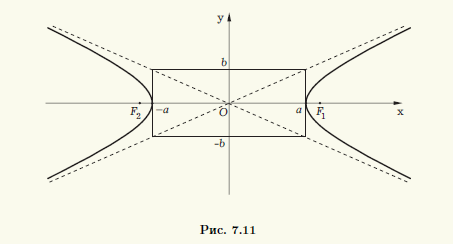
Построение гиперболы по ее действительной (2a) и мнимой (2b) осям следует начинать с прямоугольника с центром в начале координат и сторонами 2a и 2b, параллельными, соответ-ственно, действительной и мнимой осям симметрии гиперболы (рис. 7.11). Асимптоты гиперболы являются продолжениями диагоналей этого прямоугольника, а вершины гиперболы — точками пересечения сторон прямоугольника с действительной осью симметрии. Отметим, что прямоугольник и его положение на плоскости однозначно определяют форму и положение гиперболы. Отношение b/a сторон прямоугольника определяет степень сжатости гиперболы, но вместо этого параметра обычно используют эксцентриситет гиперболы. Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε. Для гиперболы, описываемой уравнением (7.8), ε = c/a. Отметим, что если эксцентриситет эллипса может принимать значения из полуинтервала [0,1) (значение 0 соответствует предельному варианту эллипса — окружности), то эксцентриситет гиперболы всегда попадает в интервал (1, + ∞).
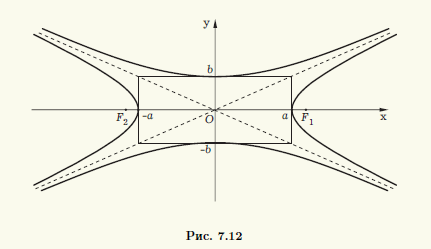
Построим прямоугольник с центром в начале системы координат Oxy и сторонами 2a, 2b, параллельными осям абсцисс и ординат соответственно. Проведем прямые y = (b/a)x и y = — (b/a)x, на которых лежат диагонали прямоугольника. Существует две гиперболы, соответствующие построенному прямоугольнику (рис. 7.12). Первая из них описывается каноническим уравнением (7.8), а вторая — уравнением
x 2 /a 2 — y 2 /b 2 = -1. (7.10)
Вторую гиперболу называют сопряженной по отношению к первой, а уравнение (7.10) — каноническим уравнением сопряженной гиперболы. Действительная и мнимая оси первой гиперболы являются соответственно мнимой и действительной осями сопряженной гиперболы, а асимптоты у них общие.
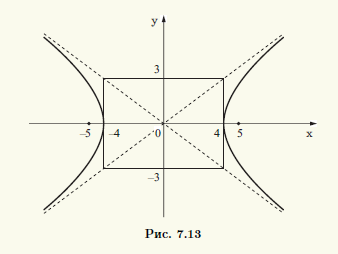
Пример 7.2. Найдем каноническое уравнение гиперболы по ее действительной полуоси a = 4 и фокальному расстоянию 2с = 10. Построим гиперболу и определим координаты ее вершин, фокусов и уравнения асимптот.
Так как действительная полуось a гиперболы известна, то, чтобы найти каноническое уравнение гиперболы, достаточно определить мнимую полуось b. Поскольку с = 5, b = √(с 2 — а 2 ), то b = √(5 2 — 4 2 ) = 3. Итак, искомое уравнение имеет вид x 2 /4 2 — y 2 /3 2 = 1. Построим прямоугольник,соответствующий заданной гиперболе (рис. 7.13). Продолжим его диагонали до асимптот ги-перболы и построим саму гиперболу. Уравнениями асимптот являются у = ±3x/4, вершины находятся в точках (±4; 0), а фокусы совпадают с точками (±5; 0).
Геометрические свойства. Геометрические свойства гиперболы во многом повторяют свойства эллипса. Вернемся к формуле (7.7). Она эквивалентна каноническому уравнению гиперболы и дает выражение для длины фокального радиуса F2M ее точки M(х; у):
|F2M| = √((х + с) 2 + у 2 ) = ±(εх + a) (7.11)
где знак плюс соответствует правой ветви гиперболы, а знак минус — левой.
Аналогично можно получить формулу для длины другого фокального радиуса, если при выводе канонического уравнения гиперболы перед первым возведением в квадрат в правую часть равенства перенести не второй, а первый квадратный радикал. При этом вместо (7.7) получим εх — a = ±√((х — с) 2 + у 2 ) , откуда
|F1M| = √((х — с) 2 + у 2 ) = ±(εх — a) (7.12)
где, как и в (7.11), знак плюс соответствует правой ветви гиперболы, а знак минус — левой. Каждое из уравнений (7.11), (7.12) является уравнением гиперболы.
Гипербола не проходит через свои фокусы (при 0 2 /c = (c 2 — a 2 )/c = b 2 /c
Гипербола также имеет и оптическое свойство, аналогичное оптическому свойству эллипса. Оно состоит в том, что лучи, вышедшие из одного фокуса, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса (рис. 7.15).
Что такое гипербола
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
- Две симметричные ветви.
- Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.
Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
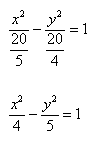
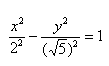
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.
Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.
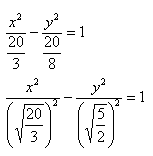
- Произведем сокращение при помощи трехэтажной дроби:
- Воспользуемся каноническим уравнением
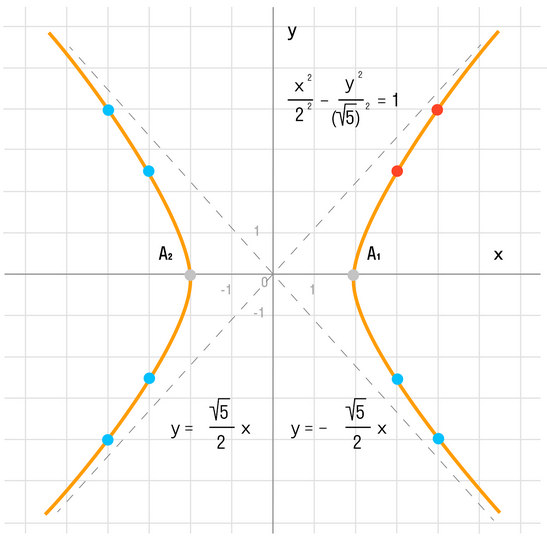
- Найдем асимптоты гиперболы. Вот так:
Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты. - Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).
- Найдем асимптоты гиперболы. Вот так:
Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
Найдем дополнительные точки — хватит двух-трех.
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
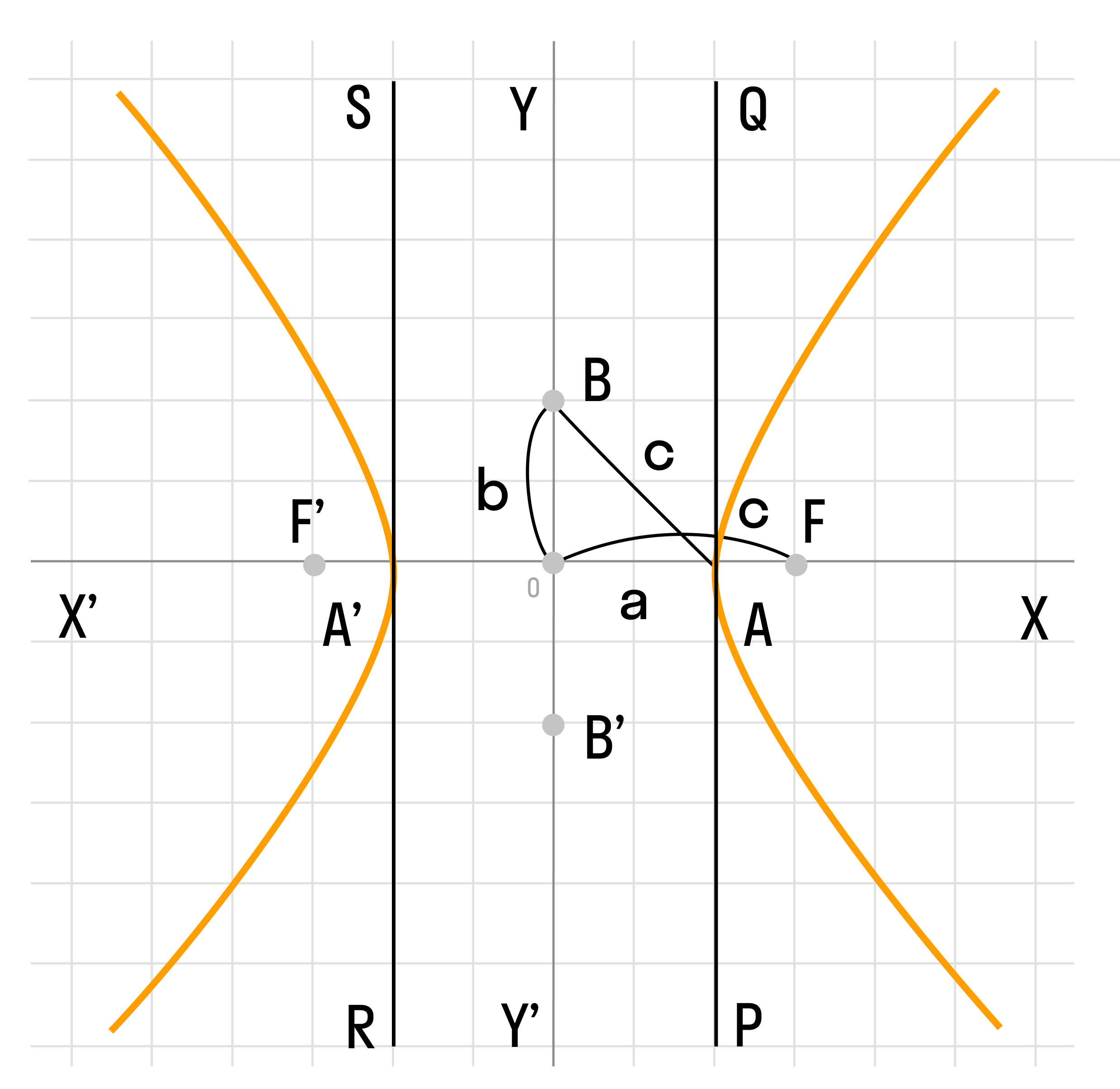
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
- пусть центр O гиперболы будет началом системы координат;
- прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
- прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Так как b^2 = c^2 — a^2, то величина b изменится.
При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2
Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.
http://hd01.ru/info/kak-najti-centr-giperboly-po-uravneniju/
http://skysmart.ru/articles/mathematic/chto-takoe-giperbola