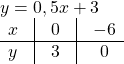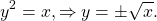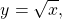Как найти уравнение функции обратной к данной

Взаимно обратные функции, основные определения, свойства, графики

Понятие обратной функции

Допустим, что у нас есть некая функция y = f ( x ) , которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x ∈ a ; b ; область ее значений y ∈ c ; d , а на интервале c ; d при этом у нас будет определена функция x = g ( y ) с областью значений a ; b . Вторая функция также будет непрерывной и строго монотонной. По отношению к y = f ( x ) она будет обратной функцией. То есть мы можем говорить об обратной функции x = g ( y ) тогда, когда y = f ( x ) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g , будут взаимно обратными.

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y = f ( x ) , которые записываются как раз с помощью этих выражений.

Нахождение взаимно обратных функций

Допустим, нам нужно найти решение уравнения cos ( x ) = 1 3 . Его решениями будут все точки: x = ± a rс c o s 1 3 + 2 π · k , k ∈ Z

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным.

Условие: какая функция будет обратной для y = 3 x + 2 ?

Решение

Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x , то есть выразив x через y .

Мы получим x = 1 3 y — 2 3 . Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:

Ответ: функция y = 1 3 x — 2 3 будет обратной для y = 3 x + 2 .

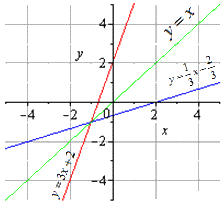
Обе взаимно обратные функции можно отобразить на графике следующим образом:

Мы видим симметричность обоих графиков относительно y = x . Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Условие: определите, какая функция будет обратной для y = 2 x .

Решение

Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0 ; + ∞ . Теперь нам нужно выразить x через y , то есть решить указанное уравнение через x . Мы получаем x = log 2 y . Переставим переменные и получим y = log 2 x .

В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

Ответ: y = log 2 x .

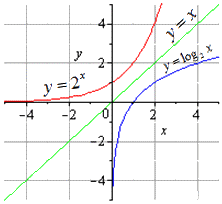
На графике обе функции будут выглядеть так:

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства функций y = f ( x ) и x = g ( y ) , являющихся взаимно обратными.

1. Первое свойство мы уже вывели ранее: y = f ( g ( y ) ) и x = g ( f ( x ) ) .
2. Второе свойство вытекает из первого: область определения y = f ( x ) будет совпадать с областью значений обратной функции x = g ( y ) , и наоборот.
3. Графики функций, являющихся обратными, будут симметричными относительно y = x .
4. Если y = f ( x ) является возрастающей, то и x = g ( y ) будет возрастать, а если y = f ( x ) убывает, то убывает и x = g ( y ) .

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать. Допустим, что у нас есть две взаимно обратные функции y = f ( x ) = a x и x = g ( y ) = log a y . Согласно первому свойству, y = f ( g ( y ) ) = a log a y . Данное равенство будет верным только в случае положительных значений y , а для отрицательных логарифм не определен, поэтому не спешите записывать, что a log a y = y . Обязательно проверьте и добавьте, что это верно только при положительном y .

А вот равенство x = f ( g ( x ) ) = log a a x = x будет верным при любых действительных значениях x .

Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, a r c sin sin 7 π 3 ≠ 7 π 3 , потому что область значений арксинуса — π 2 ; π 2 и 7 π 3 в нее не входит. Верной будет запись

a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3

А вот sin a r c sin 1 3 = 1 3 – верное равенство, т.е. sin ( a r c sin x ) = x при x ∈ — 1 ; 1 и a r c sin ( sin x ) = x при x ∈ — π 2 ; π 2 . Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

• Основные взаимно обратные функции: степенные

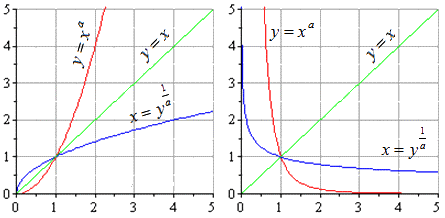
Если у нас есть степенная функция y = x a , то при x > 0 степенная функция x = y 1 a также будет обратной ей. Заменим буквы и получим соответственно y = x a и x = y 1 a .

На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

• Основные взаимно обратные функции: показательные и логарифмические

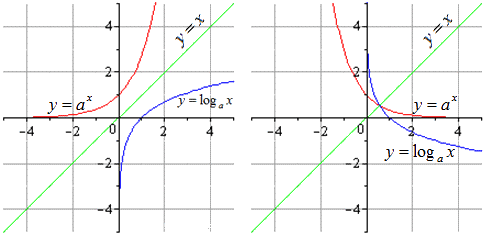
Возьмем a,которое будет положительным числом, не равным 1 .

Графики для функций с a > 1 и a 1 будут выглядеть так:

• Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

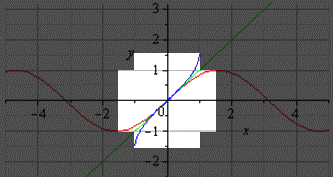
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

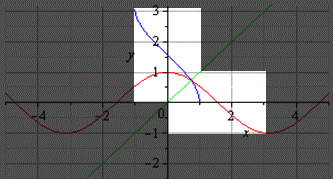
График главной ветви косинуса и арккосинуса выглядит так:

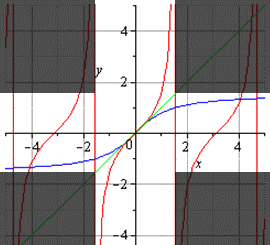
График главной ветви арктангенса и тангенса:

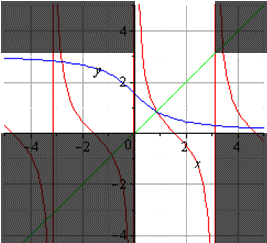
График главной ветви арккотангенса и котангенса будет таким:

Если же вам требуется построить обратные ветви, отличные от главных, то обратную тригонометрическую функцию при этом мы сдвигаем вдоль оси O y на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π 2 ; 3 π 2 , то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.

Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Взаимно обратные функции

Функция, обратная данной

По определению (см. §34 справочника для 7 класса)

Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Пусть некоторое соответствие задано таблицей:

Множество значений X = <-4;-3;…;4>отображается в множество значений Y = <-2;-1,5;…;2>: $X \xrightarrow Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.

С другой стороны, мы можем рассмотреть обратное отображение $Y \xrightarrow X$, заданное той же таблицей. При этом каждому значению y соответствует единственное значение x, т.е., обратное соответствие $g = f^<-1>$ также является функцией.

Функцию $f: X \xrightarrow Y$ с областью определения X и областью значений Y называют обратимой , если обратное ей соответствие $g: Y \xrightarrow g X$ также является фунцией.

Если функция f обратима, то обратное ей соответствие $g = f^<-1>$ называют обратной функцией к f.

Например: аналитическое выражение для функции $X \xrightarrow Y$, заданной таблицей $y = f(x) = \frac<2>$. Обратное соответствие $Y \xrightarrow X$ также является функцией x = g(y) = 2y.

Функция g — обратная функция к f.

В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac<2>$ и y=2x являются взаимно обратными.

Алгоритм вывода формулы функции, обратной данной

На входе: множества X и Y, для которых оба соответствия $X \xrightarrow Y$ и $Y \xrightarrow X$ являются функциями.

Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.

Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.

Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.

1) Пусть исходная функция $y = \frac<2>$

Шаг 1. Меняем аргумент и значение: $x = \frac<2>$

Шаг 2. Находим y из полученной формулы: y = 2x — искомая обратная функция

Шаг 3. Ограничений на x и y нет

2) Пусть исходная функция y = -2x+3

Шаг 1. Меняем аргумент и значение: x = -2y+3

Шаг 2. Находим y из полученной формулы: $y = \frac<-x+3><2>$ — искомая обратная функция

Шаг 3. Ограничений на x и y нет

3) Пусть исходная функция $y = \sqrt$

Шаг 1. Меняем аргумент и значение: $x = \sqrt$

Шаг 2. Находим y из полученной формулы: $y = x^2-1$ — искомая обратная функция

Шаг 3. На исходную функцию накладываются ограничения

на $x:x+1 \ge 0 \Rightarrow x \ge -1$, на $y:y \ge 0$

Тогда исходная функция определяется на множествах $y \ge -1$, $x \ge 0$

4) Пусть исходная функция $y = 2x^2+1$

Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$

Шаг 2. Находим y из полученной формулы: $y = \sqrt<\frac<2>>$ — искомая обратная функция

Шаг 3. На обратную функцию накладываются ограничения

на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$

Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$

Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.

Свойства взаимно обратных функций

Пусть f и g — взаимно обратные функции. Тогда:

1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.

2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.

3. Если f — нечётная, то и g — нечётная.

4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.

5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.

Графики пар взаимно обратных функций, найденных выше:

Примеры

Пример 1. Задайте формулой функцию, обратную данной.

Меняем аргумент и значение: x = 5y-4

Получаем: $y = \frac<5>$ — искомая обратная функция

Меняем аргумент и значение: x = -3y+2

Получаем: $y = \frac<-x+2><3>$ — искомая обратная функция

в) y = 4x+1, где $-1 \le x \le 5$

Меняем аргумент и значение: x = 4y+1

Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac <4>\le 5 \Rightarrow -4 \le x-1 \le 20 \Rightarrow -3 \le x \le 21$

Итак, искомая обратная функция: $y = \frac<4>$, где -3 $\le x \le 21$

г) $y=- \frac<1> <2>x+7$, где $2 \le x \le 9$

Меняем аргумент и значение: $x=-\frac<1> <2>y+7$

Получаем: y = 2(-x+7) = -2x+14

Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$

$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$

$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция

Пример 2. Найдите функцию, обратную данной.

Постройте график исходной и обратной функции в одной системе координат.

$x = y^2 \Rightarrow y = \pm \sqrt$

При этом $y \le 0$

$y = — \sqrt$ – искомая обратная функция

б) y = x-3, $-1 \le x \le 4$

$x = y-3 \Rightarrow y = x+3$

При этом $-1 \le y \le 4 \Rightarrow -1 \le x+3 \le 4$

$\Rightarrow -4 \le x \le 1$

y = x+3, $-4 \le x \le 1$ — искомая обратная

$x = \frac<1> \Rightarrow y = \frac<1> -1$

Область определения: $x \ge 3$

Область значений: $y \ge 1$

$x = 1+ \sqrt \Rightarrow y = (x-1)^2+3$

Обратная функция

Что такое обратная функция? Как найти функцию, обратную данной?

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо :

1) В формулу функции вместо y подставить x, вместо x — y:

2) Из полученного равенства выразить y через x:

Найти функцию, обратную функции y=2x-6.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

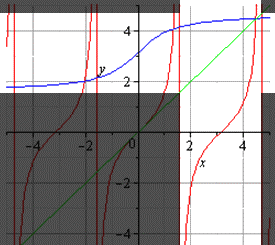
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).

Теорема (необходимое и достаточное условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.

Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).

то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:

В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.

1 комментарий

Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?