Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1.
Условие
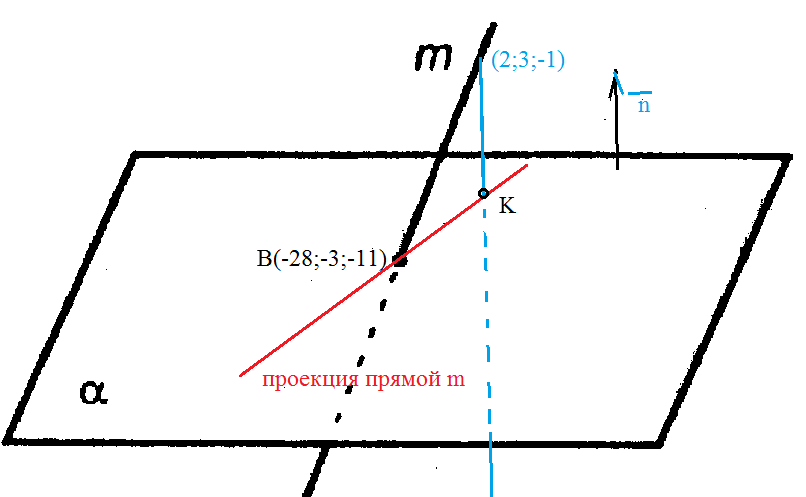
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0
Решение
Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector
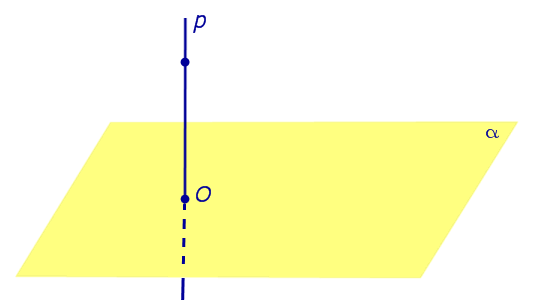
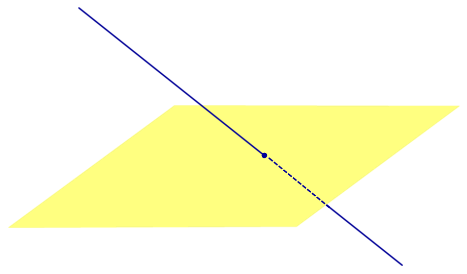
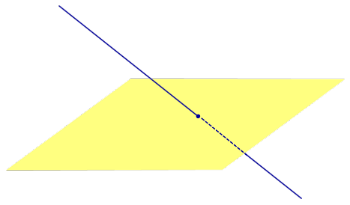
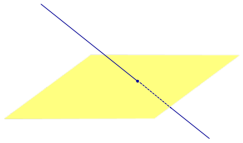
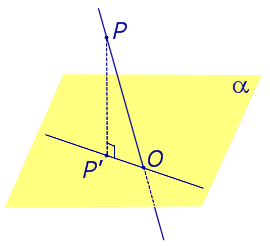
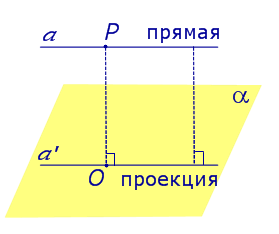
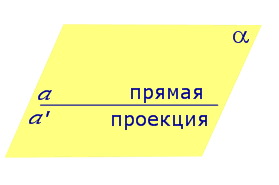
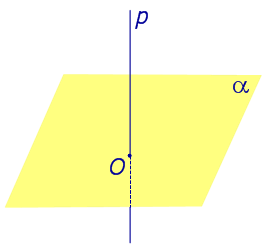
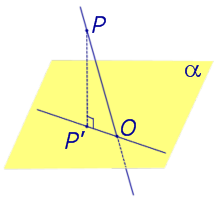
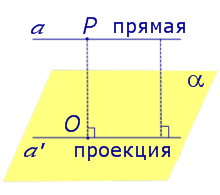
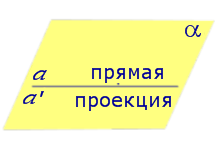
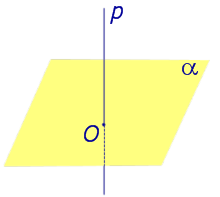
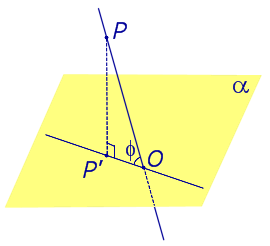
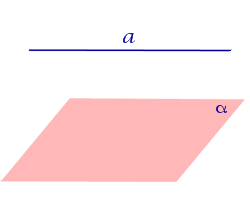
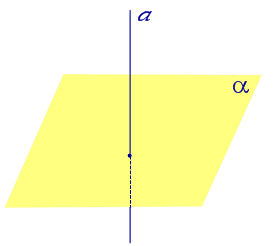
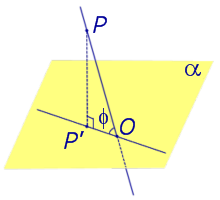
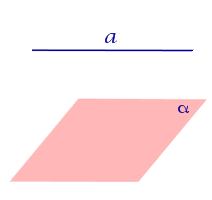
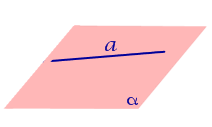
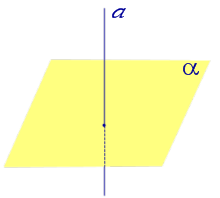
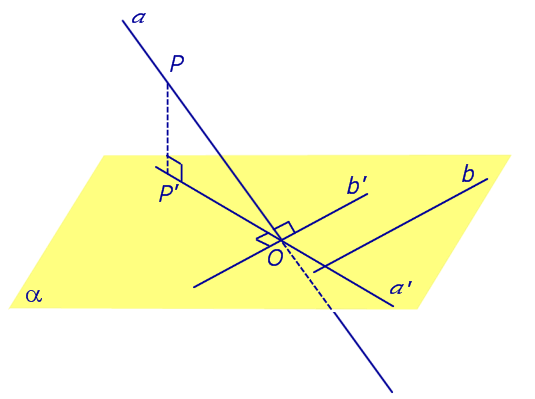
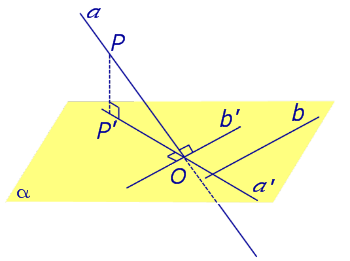
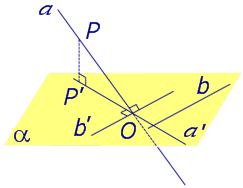
Найдем координаты точки K — точки пересечения этой прямой и плоскости Обозначим отношение подставим в уравнение плоскости Найдем координаты точки В — точки пересечения данной прямой и данной плоскости. Обозначим отношение подставим в уравнение плоскости Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки Если прямая представляется уравнениями ,где С1 и С2 одновременно не равны нулю (случай когда С1=С2= 0 рассмотрен ниже в примере 2). Чтобы найти проекцию прямой на плоскость XOY, необходимо исключить z из уравнений (1) и (2). Полученное уравнение (вместе с уравнением z=0) будет представлять искомую проекцию. Аналогично находятся проекции на плоскости для YOZ и ZOX. Пример 1 на плоскость ХОY. Решение Это уравнение вместе с уравнением z=0 представляет проекцию L’ прямой L на плоскость XOY. Пример 2 Решение Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость. Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O. Точка O является ортогональной проекцией на плоскость α каждой точки прямой p. Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма». Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость». Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α. Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2). Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α. Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO. Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α. Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α. Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO. Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α. Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице. Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. ) На рисунке это угол φ Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю. Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю. Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O ) На рисунке это угол φ Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю. Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю. Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b. Доказательство. Рассмотрим следующий рисунок 3. На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b. Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’. Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b. Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3. Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’. http://www.matematicus.ru/vysshaya-matematika/analiticheskaya-geometriya-v-prostranstve/proektsii-pryamoj-na-koordinatnye-ploskosti http://www.resolventa.ru/uslugi/uslugischoolsvib.htm
Решаем систему:
<(x-2)/1=(y-3)/4=(z-1)/(-3)
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1Проекции прямой на координатные плоскости
Найти проекцию прямой L
Для того, чтобы исключить z, умножим первое уравнение на 4, а второе — на 3 и затем сложим. Получим:
Найти проекции прямой L
2х-3у=0
х+у-4=0
на координатные плоскости.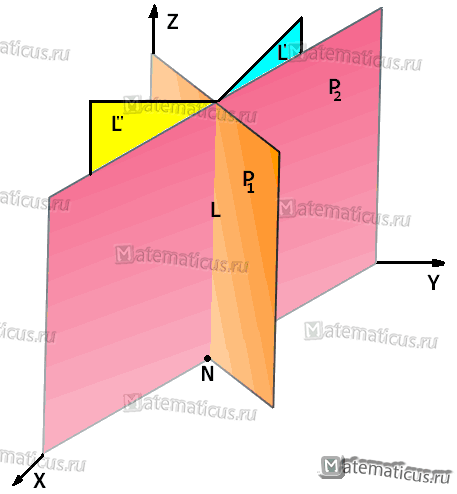
В данных уравнениях отсутствует z, потому что плоскости Р1 и Р2 перпендикулярны (Р1⊥Р2) к плоскости XOY. Прямая L перпендикулярна к XOY и проектируется на плоскость XOY в точку N с координатой zN=0. Решая систему, находим значения xN=12/5, уN=8/5.
Уравнение проекции L’ на плоскость YOZ можно найти по общему способу, исключая х из уравнения. Получим у=8/5, то есть то же равенство, которое найдено выше для уN. Уравнение проекции L» на плоскость XOZ будет x=12/5Ортогональнальная проекция прямой на плоскость.
Угол между прямой и плоскостью.
Теорема о трех перпендикулярах


Проекция прямой на плоскость
Фигура Рисунок Свойство проекции Наклонная к плоскости α Прямая, параллельная плоскости Прямая, лежащая на плоскости Прямая, перпендикулярная к плоскости Угол между прямой и плоскостью
Фигура Рисунок Определение Наклонная к плоскости α Прямая, параллельная плоскости Прямая, лежащая на плоскости Прямая, перпендикулярная к плоскости 

Теорема о трех перпендикулярах