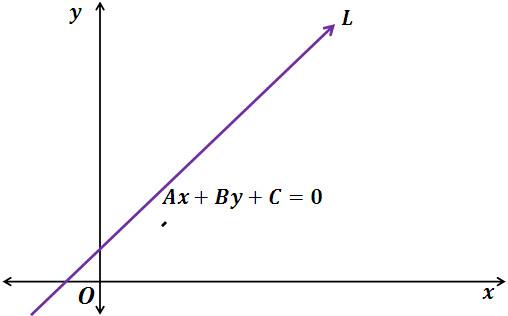Как найти вектор по уравнению плоскости

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

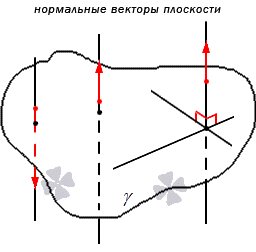
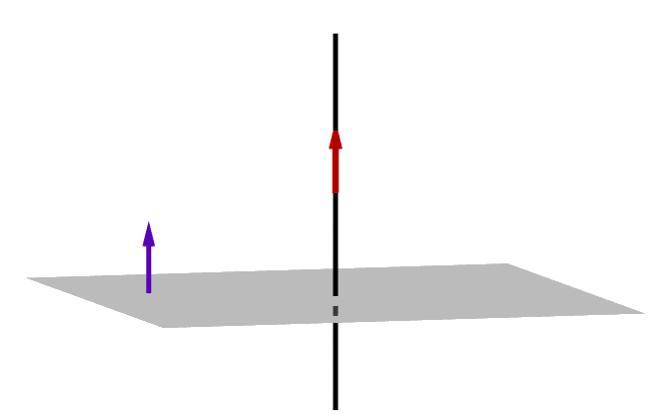
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

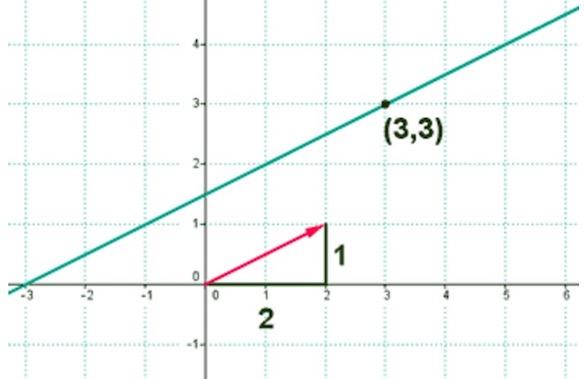
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Направляющий вектор прямой: определение и примеры

Важным геометрическим объектом, который изучают в плоском пространстве, является прямая. В трехмерном же пространстве, помимо прямой, появляется еще плоскость. Оба объекта удобно задавать с помощью направляющих векторов. Что это такое, как применяют эти вектора для определения уравнений прямой и плоскости? Эти и другие вопросы освещаются в статье.

Прямая и способы ее задавания

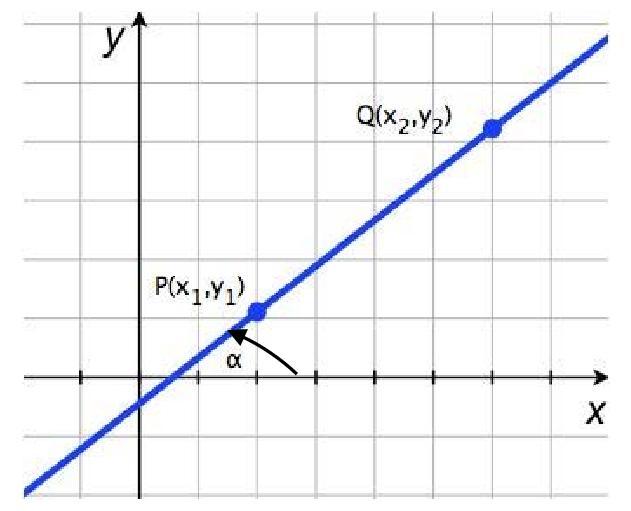
Каждый школьник хорошо представляет, о каком геометрическом объекте идет речь. С точки зрения математики, прямая представляет собой набор точек, которые в случае их попарного произвольного соединения между собой приводят к получению совокупности параллельных векторов. Это определение прямой используют для написания уравнения для нее как в двумерном, так и в трехмерном пространстве.

Вам будет интересно: Шаболда — это слово с непростой судьбой

Для описания рассматриваемого одномерного объекта пользуются разными видами уравнений, которые перечислены в списке ниже:

• общего вида;
• параметрическое;
• векторное;
• каноническое или симметричное;
• в отрезках.

Каждый из названных видов имеет некоторые преимущества по отношению к другим. Например, уравнением в отрезках удобно пользоваться при изучении поведения прямой относительно осей координат, уравнение общего вида удобно при нахождении направления, перпендикулярного заданной прямой, а также при вычислении угла ее пересечения с осью x (для плоского случая).

Вам будет интересно: Телескопы рефлекторные: описание, устройство, история создания

Поскольку тема данной статьи связана с направляющим вектором прямой, то далее будем рассматривать только уравнение, где этот вектор является принципиальным и содержится явно, то есть векторное выражение.

Задание прямой через вектор

Предположим, что у нас имеется некоторый вектор v¯ с известными координатами (a; b; c). Поскольку координат три, то вектор задан в пространстве. Как изобразить его в прямоугольной системе координат? Делается это очень просто: на каждой из трех осей откладывается отрезок, длина которого равна соответствующей координате вектора. Точка пересечения трех перпендикуляров, восстановленных к плоскостям xy, yz и xz, будет концом вектора. Началом же его является точка (0; 0; 0).

Тем не менее приведенное положение вектора не является единственным. Аналогичным образом можно нарисовать v¯, располагая его начало в произвольной точке пространства. Эти рассуждения говорят о том, что задать конкретную прямую с помощью вектора нельзя. Он задает семейство из бесконечного числа параллельных прямых.

Вам будет интересно: Формула угла между плоскостью и прямой. Примеры использования формулы

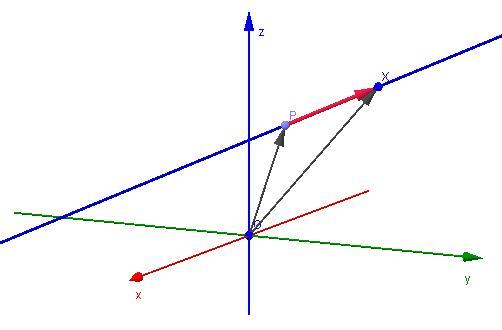
Теперь зафиксируем некоторую точку P(x0; y0; z0) пространства. И зададим условие: через P должна проходить прямая. В этом случае вектор v¯ тоже должен содержать эту точку. Последний факт означает, что можно задать одну единственную прямую, используя P и v¯. Она запишется в виде следующего уравнения:

Здесь Q — любая точка, принадлежащая прямой. Эту точку можно получить, подобрав соответствующий параметр λ. Записанное уравнение называется векторным, а v¯ получил название направляющего вектора прямой. Располагая его так, чтобы он проходил через P, и изменяя его длину с помощью параметра λ, мы получаем каждую точку Q прямой.

В координатной форме уравнение запишется так:

(x; y; z) = (x0; y0; z0) + λ × (a; b; c)

И в явном (параметрическом) виде можно записать:

Если в приведенных выражениях исключить третью координату, то мы получим векторные уравнения прямой на плоскости.

Для каких задач полезно знать направляющий вектор ?

Как правило, это задачи на определение параллельности и перпендикулярности прямых. Также определяющий направление прямой вектор используется при вычислении дистанции между прямыми и точкой и прямой, для описания поведения прямой относительно плоскости.

Две прямые будут параллельными, если таковыми являются их направляющие вектора. Соответственно, перпендикулярность прямых доказывается с помощью перпендикулярности их векторов. В этих типах задач достаточно рассчитать скалярное произведение рассматриваемых векторов, чтобы получить ответ.

В случае задач на вычисление расстояний между прямыми и точками направляющий вектор входит явно в соответствующую формулу. Запишем ее:

Здесь P1P2¯ — построенный на точках P1 и P2 направленный отрезок. Точка P2 является произвольной, лежащей на прямой с вектором v¯, точка же P1 является той, до которой следует определить расстояние. Она может быть как самостоятельной, так и принадлежать другой прямой или плоскости.

Отметим, что рассчитывать расстояние между прямыми имеет смысл только тогда, когда они являются параллельными или скрещивающимися. Если же они пересекаются, то d равно нулю.

Приведенная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой, только в этом случае P1 должна принадлежать плоскости.

Решим несколько задач, чтобы нагляднее показать, как пользоваться рассматриваемым вектором.

Задача на составление векторного уравнения

Известно, что прямая описывается следующим равенством:

Следует написать соответствующее выражение в векторной форме.

Это типичное уравнение прямой, известное каждому школьнику, записано в общем виде. Покажем, как его переписать в векторной форме.

Выражение можно представить в виде:

Видно, что если его раскрыть, то получится исходное равенство. Теперь разделим его правую часть на два вектора так, чтобы только один из них содержал иксы, имеем:

(x; y) = (x; 3 × x) + (0; -4)

Остается вынести x за скобки, обозначить его греческим символом и поменять вектора правой части местами:

(x; y) = (0; -4) + λ × (1; 3)

Мы получили векторную форму записи исходного выражения. Координаты направляющего вектора прямой равны (1; 3).

Задача на определение взаимного расположения прямых

В пространстве заданы две прямые:

(x; y; z) = (1; 0; -2) + λ × (-1; 3; 1);

(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)

Они являются параллельными, скрещивающимися или пересекающимися?

Ненулевые вектора (-1; 3; 1) и (1; 2; 0) будут направляющими для этих прямых. Выразим в параметрической форме эти уравнения и подставим координаты первого во второе. Получаем:

x = 3 + γ = 1 — λ => γ = -2 — λ;

y = 2 + 2 × γ = 3 × λ => γ = 3 / 2 × λ — 1;

z = 2 = -2 + λ => λ = 4

Подставляем найденный параметр λ в два уравнения выше, получаем:

γ = 3 / 2 × λ — 1 = 5

Параметр γ не может одновременно принимать два разных значения. Это означает, что прямые не имеют ни одной общей точки, то есть являются скрещивающимися. Параллельными они не являются, так как ненулевые векторы не параллельны друг другу (для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго).

Математическое описание плоскости

Для задания плоскости в пространстве приведем уравнение общего вида:

A × x + B × y + C × z + D = 0

Здесь латинские большие буквы представляют собой конкретные числа. Первые три из них определяют координаты нормального вектора плоскости. Если его обозначить n¯, тогда:

Этот вектор является перпендикулярным плоскости, поэтому его называют направляющим. Его знание, а также известные координаты какой-либо точки, принадлежащей плоскости, однозначно задают последнюю.

Если точка P(x1; y1; z1) плоскости принадлежит, тогда свободный член D рассчитывается следующим образом:

D = -1 × (A × x1 + B × y1 + C × z1)

Решим пару задач с использованием общего уравнения для плоскости.

Задача на нахождение нормального вектора плоскости

Плоскость задана в следующем виде:

(y — 3) / 2 + (x + 1) / 3 — z / 4 = 1

Как найти направляющий вектор для нее?

Из приведенной выше теории следует, что координаты нормального вектора n¯ являются коэффициентами, стоящими перед переменными. В связи с этим для нахождения n¯ следует записать уравнение в общем виде. Имеем:

1 / 3 × x + 1 / 2 × y — 1 / 4 × z — 13 / 6 = 0

Тогда нормальный вектор плоскости равен:

Задача на составление уравнения плоскости

Даны координаты трех точек:

Как будет выглядеть уравнение плоскости, содержащей все эти точки.

Через три точки, которые одной прямой не принадлежат, можно провести только одну плоскость. Чтобы найти ее уравнение, сначала вычислим направляющий вектор плоскости n¯. Для этого поступим следующим образом: найдем произвольные два вектора, принадлежащие плоскости, и вычислим их векторное произведение. Оно даст вектор, который этой плоскости будет перпендикулярен, то есть n¯. Имеем:

M1M2¯ = (1; -1; 5); M1M3¯ = (-1; -2; -2);

n¯ = [M1M2¯ × M1M3¯] = (12; -3; -3)

Возьмем точку M1 для составления выражения плоскости. Получаем:

D = -1 × (12 × 1 + (-3) × 0 + (-3) × 0) = -12;

12 × x — 3 × y — 3 × z — 12 = 0 =>

4 × x — y — z — 4 = 0

Мы получили выражение общего типа для плоскости в пространстве, определив сначала направляющий вектор для нее.

Свойство векторного произведения следует запомнить при решении задач с плоскостями, поскольку оно позволяет простым способом определять координаты нормального вектора.