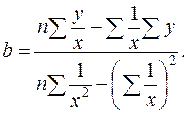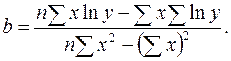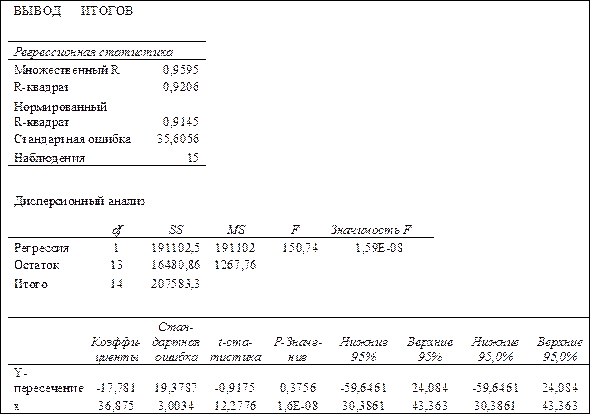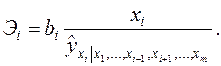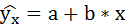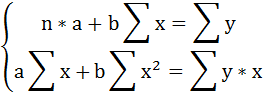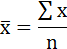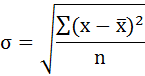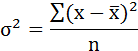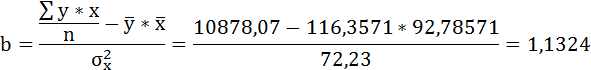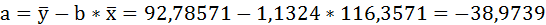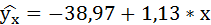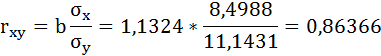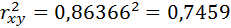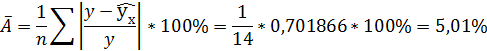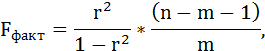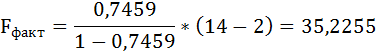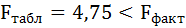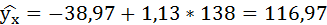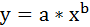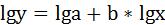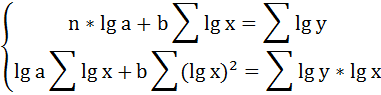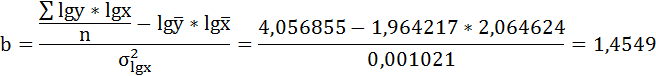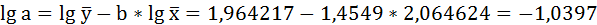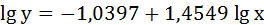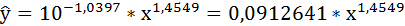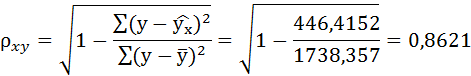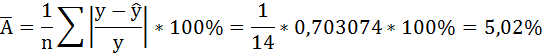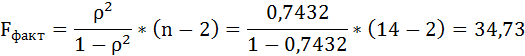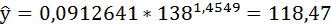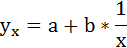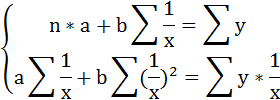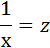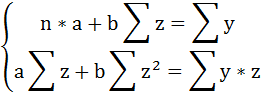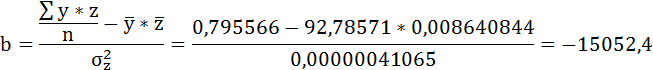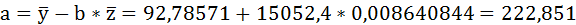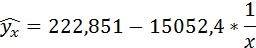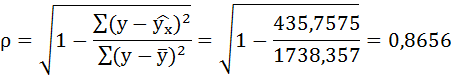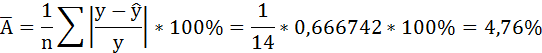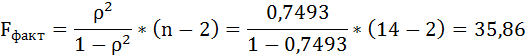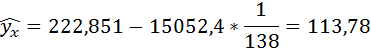Как найти вид прогнозного уравнения

Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения Затем вычисляется средняя стандартная ошибка прогноза

где

и строится доверительный интервал прогноза

Интервал может быть достаточно широк за счет малого объема наблюдений.

Регрессии, нелинейные по включенным переменным, приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью МНК.

Гиперболическая регрессия:

Линеаризующее преобразование:

Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: внутренне нелинейные и т.п. (к линейному виду не приводятся) и внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований), например:

Экспоненциальная регрессия:

Линеаризующее преобразование:

Степенная регрессия:

Линеаризующее преобразование:

Показательная регрессия:

Линеаризующее преобразование:

Логарифмическая регрессия:

Линеаризующее преобразование:

2. Решение типовых задач

Пример 1.1. По 15 предприятиям отрасли (табл. 1.1) известны: – объем произведенной продукции (тыс. ед.) и – затраты на выпуск этой продукции (тыс. ден. ед.). Необходимо:

1) определить зависимость от

2) построить корреляционные поля и график уравнения линейной регрессии на

3) сделать вывод о качестве модели и рассчитать прогнозное значение при прогнозном значении составляющем 107% от среднего уровня.

Решение:

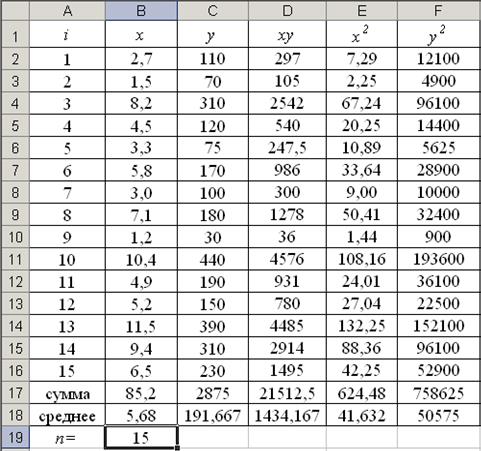
1) В Excel составим вспомогательную таблицу 1.2.

Вычислим количество измерений Для этого в ячейку В19 поместим =СЧЁТ(A2:A16).

С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех (ячейка В17) и (ячейка С17).

Вычислим выборочные средние: =5,68; =191,67. Таким образом, средний объем произведенной продукции по 15 предприятиям отрасли составляет 5,68 тыс. ед., а средние затраты на выпуск этой продукции – 191,67 тыс. ден. ед.

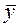
Заполним столбцы D, E, F. Например, в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.

Для вычисления выборочной ковариациимежду и используем формулу т.е. в ячейку B21 поместим =D18-B18*C18 и получим 345,5 (рис. 1.1).

Выборочную дисперсиюдля найдем по формуле т.е. в ячейку B22 поместим =E18-B18*B18 и получим 9,37 (рис. 1.1). Аналогично определяем =13838,89.

Рис. 1.1. Решение примера 1.1 в Excel

Выборочный коэффициент корреляции =0,96 очень высокий, что указывает на прямую и весьма сильную связь между и т.е. с ростом объема произведенной продукции увеличиваются затраты на выпуск этой продукции

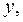
Выборочный коэффициент линейной регрессии =36,87; параметр =-17,78. Значит, уравнение парной линейной регрессии имеет вид =-17,78+36,87

Коэффициент показывает, что при увеличении объема произведенной продукции на 1 тыс. ед. затраты на выпуск этой продукции в среднем увеличатся на 36,87 тыс. ден. ед.

2) Подставляя в найденное уравнение регрессии фактические значения определим теоретические (расчетные) значения в столбце G.

С помощью Мастера диаграмм строим корреляционные поля (выделяя столбцы со значениями и ) и уравнение линейной регрессии (выделяя столбцы со значениями и ). Выбираем тип диаграммы – Точечная и, следуя рекомендациям Мастера диаграмм, вводим нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим рис. 1.2.

Рис. 1.2. График зависимости объема произведенной продукции
от теоретических и фактических затрат на выпуск этой продукции

3) Для оценки качества построенной модели регрессии вычислим:

• коэффициент детерминации =0,92, который показывает, что изменение затрат на выпуск продукции на 92% объясняется изменением объема произведенной продукции а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;

• среднюю ошибку аппроксимации. Для этого в столбце H вычислим а в столбце I – выражение (рис. 1.1). При умножении среднего значения (ячейка I18) на 100% получим 18,2%. Следовательно, в среднем теоретические значения отклоняются от фактических на 18,2%.

С помощью -критерия Фишераоценим значимость уравнения регрессии в целом: 150,74.

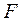
На уровне значимости 0,05 =4,67 определяем по таблице -крите­рия Фишера (таблица 1 приложения) либо с помощью встроенной статистической функции FРАСПОБР (рис. 1.3).

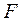
Так как то уравнение регрессии значимо при =0,05.

Рис. 1.3. Диалоговое окно функции FРАСПОБР

Средний коэффициент эластичности =1,09 показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1,09%.

Рассчитаем прогнозное значение путем подстановки в уравнение регрессии =-17,78+36,87 прогнозного значения фактора = 1,07=6,08. Получим =206,33. Следовательно, при выпуске продукции в количестве 6,08 тыс. ед. затраты на производство этой продукции составят 206,33 тыс. ден. ед.

Найдем =35,606 поместив в ячейку F23 =КОРЕНЬ(J17/(B19-2)).

Средняя стандартная ошибка прогноза:

=36,79.

На уровне значимости =0,05 либо по таблице —критерия Стьюдента (таблица 2 приложения) либо с помощью встроенной статистической функции СТЬЮДРАСПОБР определим =2,1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать =79,48.

Доверительный интервал прогноза:

206,33-79,48 206,33+79,48 или 126,85 285,81.

Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет =2,25 раза. Это произошло за счет малого объема наблюдений.

3. Решение задач с помощью электронных таблиц Excel

Решение эконометрических задач можно упростить, используя встроенные функции. Активизируем Мастер функций любым из способов:

• в главном меню выбрать Вставка / Функция;

• на панели инструментов Стандартная щелкнуть по кнопке Вставка функции.

Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.

Выборочная ковариациямежду и находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.

Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).

Выборочный коэффициент корреляции между и вычисляется с помощью статистической функции КОРРЕЛ(массив X;массив Y).

Параметры линейной регрессии в Excel можно определить несколькими способами.

1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:

1. Выделить область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 – для получения только коэффициентов регрессии.

2. С помощью Мастера функций среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 1.4):

Рис. 1.4. Диалоговое окно ввода аргументов функции ЛИНЕЙН

Известные_значения_y – диапазон, содержащий данные результативного признака Y;

Известные_значения_x – диапазон, содержащий данные объясняющего признака X;

Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;

Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.

3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу , а затем – на комбинацию клавиш + + .

Дополнительная регрессионная статистика будет выведена в виде (табл. 1.3):

Значение коэффициента	Значение коэффициента
Среднеквадратическое отклонение	Среднеквадратическое отклонение
Коэффициент детерминации	Среднеквадратическое отклонение
-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

В результате применения функции ЛИНЕЙНполучим:

(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:

1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню нужно выбрать Сервис / Настройки и напротив Пакета анализа установить флажок.

2. Выбрать в главном меню Сервис / Анализ данных / Регрессия и заполнить диалоговое окно (рис. 1.5):

Входной интервал Y – диапазон, содержащий данные результативного признака Y;

Входной интервал X – диапазон, содержащий данные объясняющего признака X;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.

Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне. В результате получим итоги как на рис. 1.6.

Рис. 1.5. Диалоговое окно ввода параметров инструмента Регрессии

Рис. 1.6. Результаты применения инструмента Регрессия

В Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1. Необходимо выделить область построения диаграммы и в главном меню выбрать Диаграмма / Добавить линию тренда.

2. В появившемся диалоговом окне (рис. 1.7) выбрать вид линии тренда и задать соответствующие параметры.

Рис. 1.7. Диалоговое окно типов линии тренда

Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.

Выбираем Линейная для построения уравнения линейной регрессии.

В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину установив соответствующие флажки на закладке Параметры (рис. 1.8).

В результате получим линейный тренд (рис. 1.9).

Рис. 1.8. Диалоговое окно параметров линии тренда

Рис. 1.9. Линейный тренд

Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.

Ii. Модель множественной регрессии

1. Основные определения и формулы

Множественная регрессия– регрессия между переменными и т.е. модель вида:

где – зависимая переменная (результативный признак);

– независимые объясняющие переменные;

– возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов;

– число параметров при переменных

Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Уравнение множественной линейной регрессиив случае независимых переменных имеет вид а в случае двух независимых переменных – (двухфакторное уравнение).

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов. Строится система нормальных уравнений:

Решение этой системы позволяет получить оценки параметров регрессии с помощью метода определителей

…,

где – определитель системы;

– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными правой части системы.

Для двухфакторного уравнения коэффициенты множественной линейной регрессии можно вычислить по формулам:

Частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии 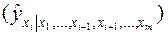определять частные коэффициенты эластичности:

Средние коэффициентами эластичности показывают на сколько процентов в среднем изменится результат при изменении соответствующего фактора на 1%:

Их можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Тесноту совместного влияния факторов на результат оценивает коэффициент (индекс) множественной корреляции:

Величина индекса множественной корреляции лежит в пределах от 0 до 1 и должна быть больше или равна максимальному парному индексу корреляции:

Чем ближе значение индекса множественной корреляции к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности (величина индекса множественной корреляции существенно отличается от индекса парной корреляции) включения в уравнение регрессии того или иного фактора.

При линейной зависимости совокупный коэффициент множественной корреляции определяется через матрицу парных коэффициентов корреляции:

где – определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

Частные коэффициенты корреляциихарактеризуют тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Если вычисляется, например, (частный коэффициент корреляции между и при фиксированном влиянии ), это означает, что определяется количественная мера линейной зависимости между и которая будет иметь место, если устранить влияние на эти признаки фактора

Частные коэффициенты корреляции, измеряющие влияние на фактора при неизменном уровне других факторов, можно определить как:

или по рекуррентной формуле:

Для двухфакторного уравнения:

или

Частные коэффициенты корреляции изменяются в пределах от -1 до +1.

Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции получится меньше, чем соответствующий парный коэффициент значит взаимосвязь признаков и в некоторой степени обусловлена воздействием на них фиксируемой переменной И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная ослабляет своим воздействием связь и

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, – коэффициент частной корреляции первого порядка.

Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент множественной корреляции:

Качество построенной модели в целом оценивает коэффициент (индекс) множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции: Индекс множественной детерминации фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как

Если число параметров при близко к объему наблюдений, то коэффициент множественной корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс множественной корреляции, который содержит поправку на число степеней свободы:

Чем больше величина тем сильнее различия и

Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным = — -2.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 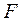—критерия Фишера:

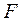
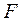
Мерой для оценки включения фактора в модель служит частный -крите­рий. В общем виде для фактора частный -критерий определяется как

Для двухфакторного уравнения частные -критерии имеют вид:

Если фактическое значение превышает табличное, то дополнительное включение фактора в модель статистически оправданно и коэффициент чистой регрессии при факторе статистически значим. Если же фактическое значение меньше табличного, то фактор нецелесообразно включать в модель, а коэффициент регрессии при данном факторе в этом случае статистически незначим.

Для оценки значимости коэффициентов чистой регрессии по -крите­рию Стьюдента используется формула:

где – коэффициент чистой регрессии при факторе

– средняя квадратическая (стандартная) ошибка коэффициента регрессии которая может быть определена по формуле:

При дополнительном включении в регрессию нового фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если это не так, то включаемый в анализ новый фактор не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по -критерию Стьюдента.

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарностифакторов. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель, тем меньше мультиколлинеарность факторов.

Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора остатки имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. При нарушении гомоскедастичности выполняются неравенства

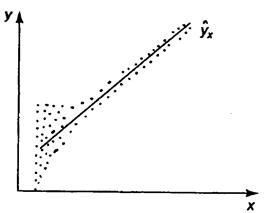
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 2.1).

Рис. 2.1.Примеры гетероскедастичности:

а) дисперсия остатков растет по мере увеличения

б) дисперсия остатков достигает максимальной величины при средних значениях переменной и уменьшается при минимальных и максимальных значениях

в) максимальная дисперсия остатков при малых значениях и дисперсия остатков однородна по мере увеличения значений

Для проверки выборки на гетероскедастичность можно использовать метод Гольдфельда-Квандта (при малом объеме выборки) или критерий Бартлетта (при большом объеме выборки).

Последовательность применения теста Гольдфельда-Квандта:

1) Упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.

2) Исключить из рассмотрения центральных наблюдений. При этом где – число оцениваемых параметров. Из экспериментальных расчетов для случая однофакторного уравнения регрессии рекомендовано при =30 принимать =8, а при =60 соответственно =16.

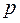
3) Разделить совокупность из наблюдений на две группы (соответственно с малыми и большими значениями фактора ) и определить по каждой из групп уравнение регрессии.

4) Вычислить остаточную сумму квадратов для первой и второй групп и найти их отношение где При выполнении нулевой гипотезы о гомоскедастичности отношение будет удовлетворять -критерию Фишера со степенями свободы для каждой остаточной суммы квадратов. Чем больше величина превышает тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

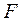
Если необходимо включить в модель факторы, имеющие два или более качественных уровней (пол, профессия, образование, климатические условия, принадлежность к определенному региону и т.д.), то им должны быть присвоены цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные называют фиктивными (искусственными) переменными.

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. Значимость влияния фиктивной переменной проверяется с помощью -критерия Стьюдента.

2. Решение типовых задач

Пример 2.1. По 15 предприятиям отрасли (табл. 2.1) изучается зависимость затрат на выпуск продукции (тыс. ден. ед.) от объема произведенной продукции (тыс. ед.) и расходов на сырье (тыс. ден. ед). Необходимо:

1) Построить уравнение множественной линейной регрессии.

2) Вычислить и интерпретировать:

• средние коэффициенты эластичности;

• парные коэффициенты корреляции, оценить их значимость на уровне 0,05;

• частные коэффициенты корреляции;

• коэффициент множественной корреляции, множественный коэффициент детерминации, скорректированный коэффициент детерминации.

3) Оценить надежность построенного уравнения регрессии и целесообразность включения фактора после фактора и после

Решение:

1) В Excel составим вспомогательную таблицу 2.2.

Аналогично примеру 1.1 вычислим: =345,5; =13838,89; =8515,78; =219,315; =9,37; =6558,08.

Затем найдем коэффициенты множественной линейной регрессии и оформим вывод результатов как на рис. 2.2.

Например, для вычисления значения коэффициента в ячейку F20 поместим формулу =(B20*B24-B21*B22)/(B23*B24-B22*B22) и получим 29,83. В ячейке F21 найдем =0,3 как =(B21*B23-B20*B22)/(B23*B24-B22*B22). Коэффициент =-13,02 вычислим по формуле =D18-B18*F20-C18*F21.

Уравнение множественной линейной регрессии примет вид:

=-13,02+29,83 +0,3

Таким образом, при увеличении объема произведенной продукции на 1 тыс. ед. затраты на выпуск этой продукции в среднем увеличатся на 29,83 тыс. ден. ед., а при увеличении расходов на сырье на 1 тыс. ден. ед. затраты увеличатся в среднем на 0,3 тыс. ден. ед.

Рис. 2.2. Решение примера 2.1 в Excel

2) Для вычисления средних коэффициентов эластичности воспользуемся формулой: Вычисляем: =0,88 и =0,18. Т.е. увеличение только объема произведенной продукции (от своего среднего значения) или только расходов на сырье на 1% увеличивает в среднем затраты на выпуск продукции на 0,88% или 0,18% соответственно. Таким образом, фактор оказывает большее влияние на результат, чем фактор

Найдем значения парных коэффициентов корреляции:

=0,96; =0,89;

=0,88.

Значения парных коэффициентов корреляции указывают на весьма тесную связь с и на тесную связь с В то же время межфакторная связь очень сильная ( =0,88>0,7), что говорит о том, что один из факторов является неинформативным, т.е. в модель необходимо включать или или

Значимость парных коэффициентов корреляции оценим с помощью -критерия Стьюдента. =2,1604 определяем по таблице —критерия Стьюдента (таблица 2 приложения) взяв =0,05 и = -2=13 либо с помощью встроенной статистической функции СТЬЮДРАСПОБР с такими же параметрами.

Фактическое значение -критерия Стьюдента для каждого парного коэффициента определим по формулам: Получим =12,28; =7,19; =6,84.

Так как фактические значения -статистики превосходят табличные, то парные коэффициенты корреляции не случайно отличаются от нуля, а статистически значимы.

Вычислим частные коэффициенты корреляции по формулам:

Получим =0,38; =0,34; =0,21. Таким образом, фактор оказывает немного более сильное влияние на результат, чем

При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за сильной межфакторной связи коэффициенты парной и частной корреляции отличаются довольно значительно.

Инструменты прогнозирования в Microsoft Excel

Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.

Процедура прогнозирования

Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.

Способ 1: линия тренда

Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.

Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

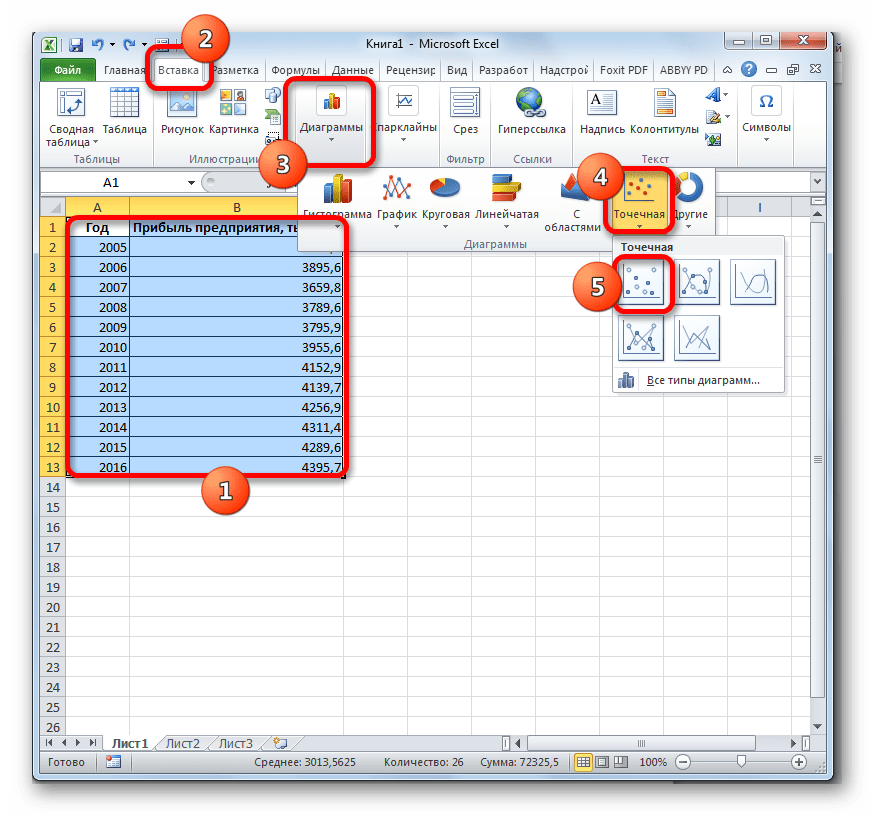
Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.

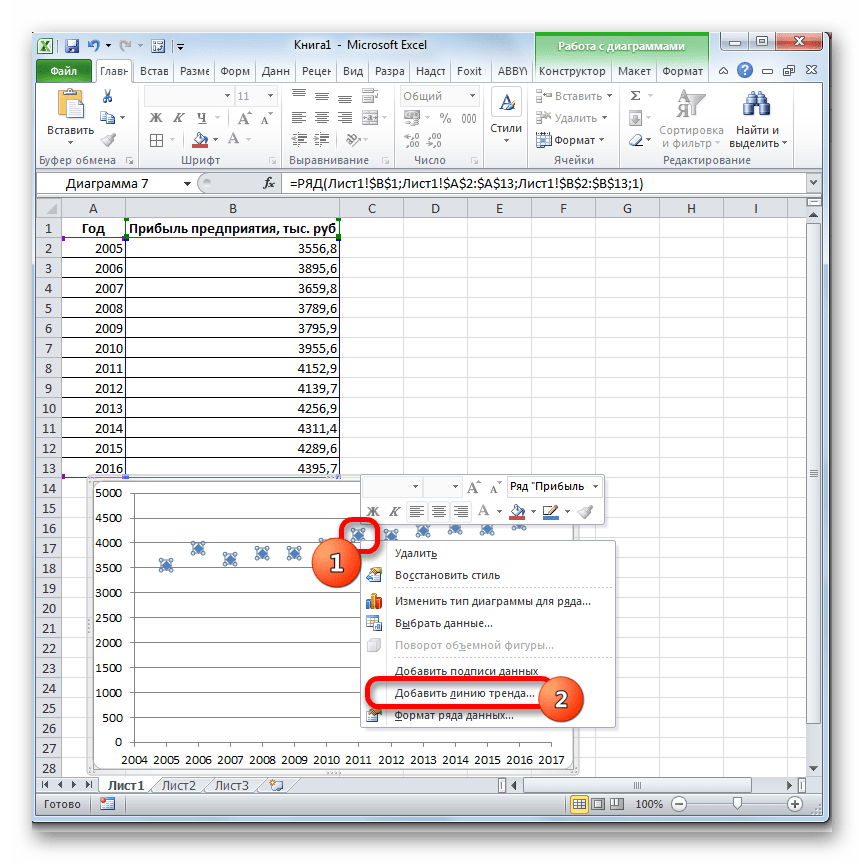
Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».

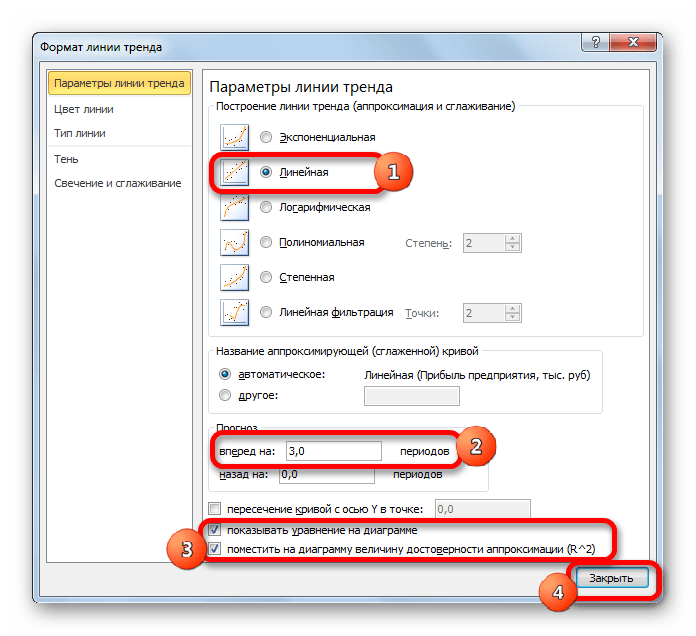
Давайте для начала выберем линейную аппроксимацию.

В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».

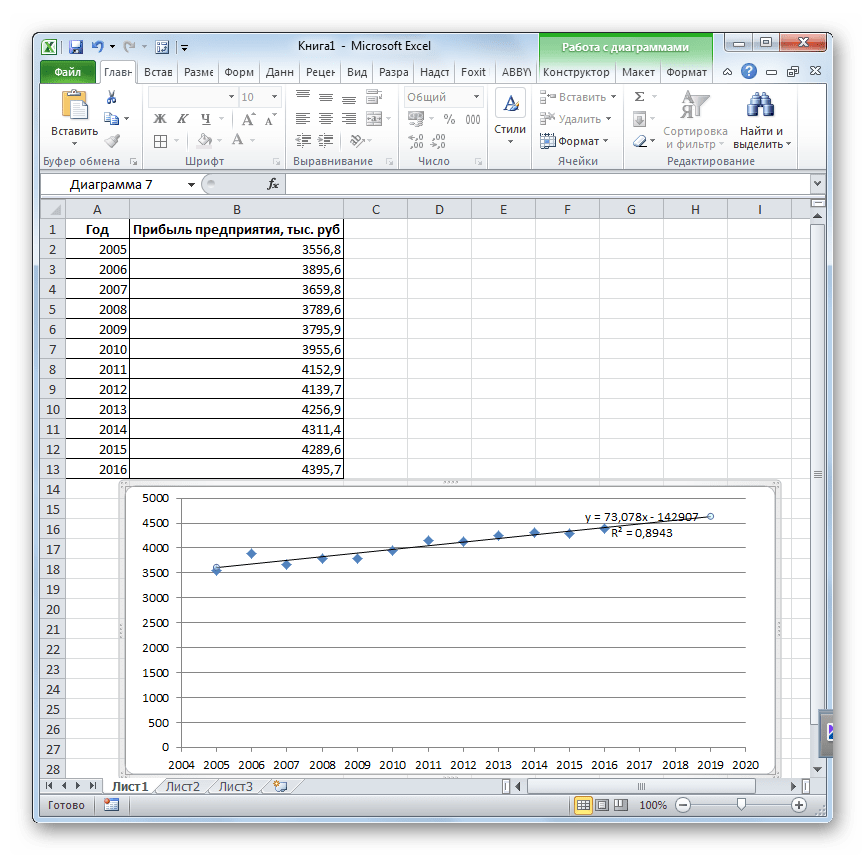
Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.

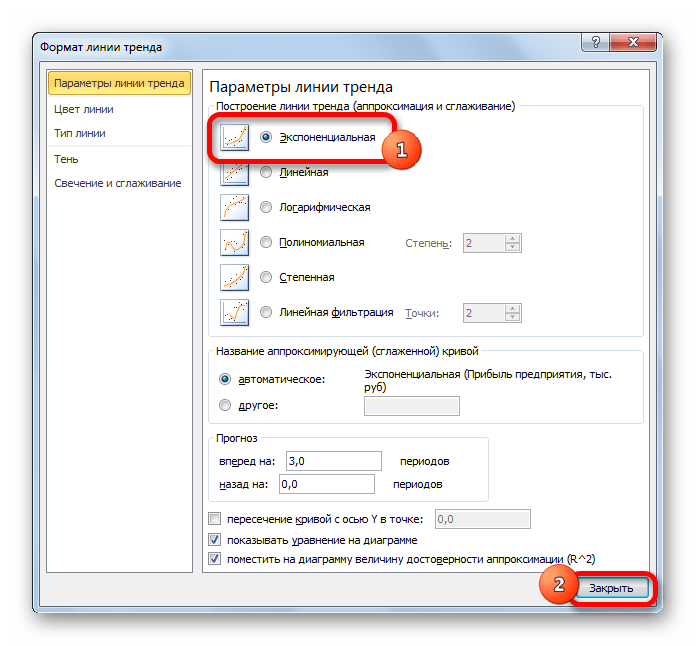
Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.

Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.

Способ 2: оператор ПРЕДСКАЗ

Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:

«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.

«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.

«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.

Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.

При вычислении данным способом используется метод линейной регрессии.

Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.

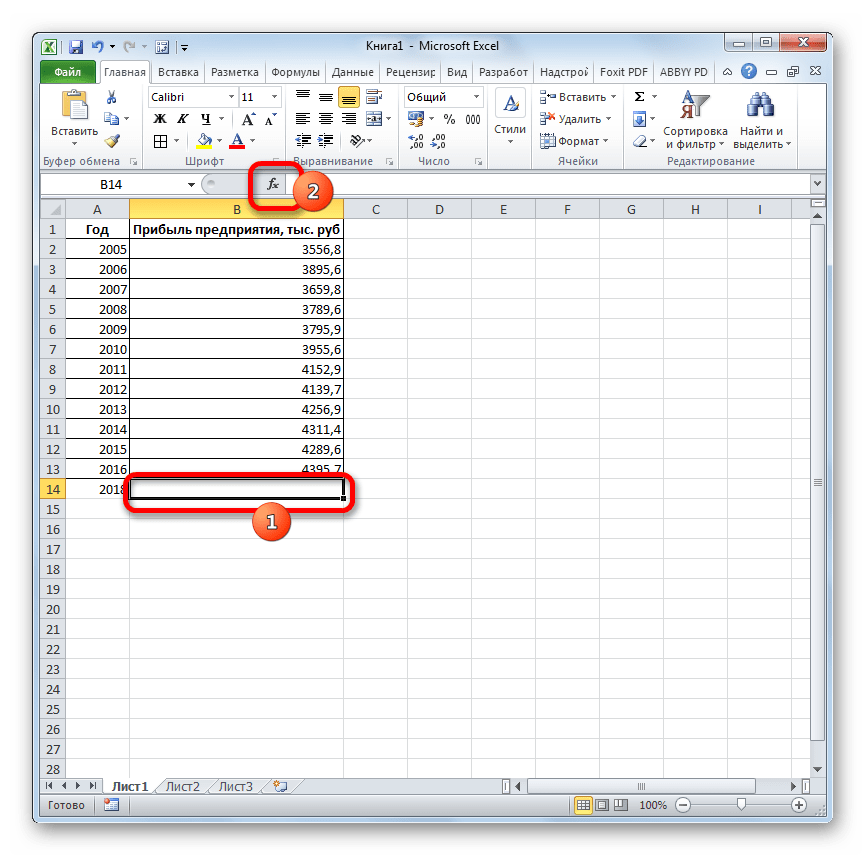
Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».

Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».

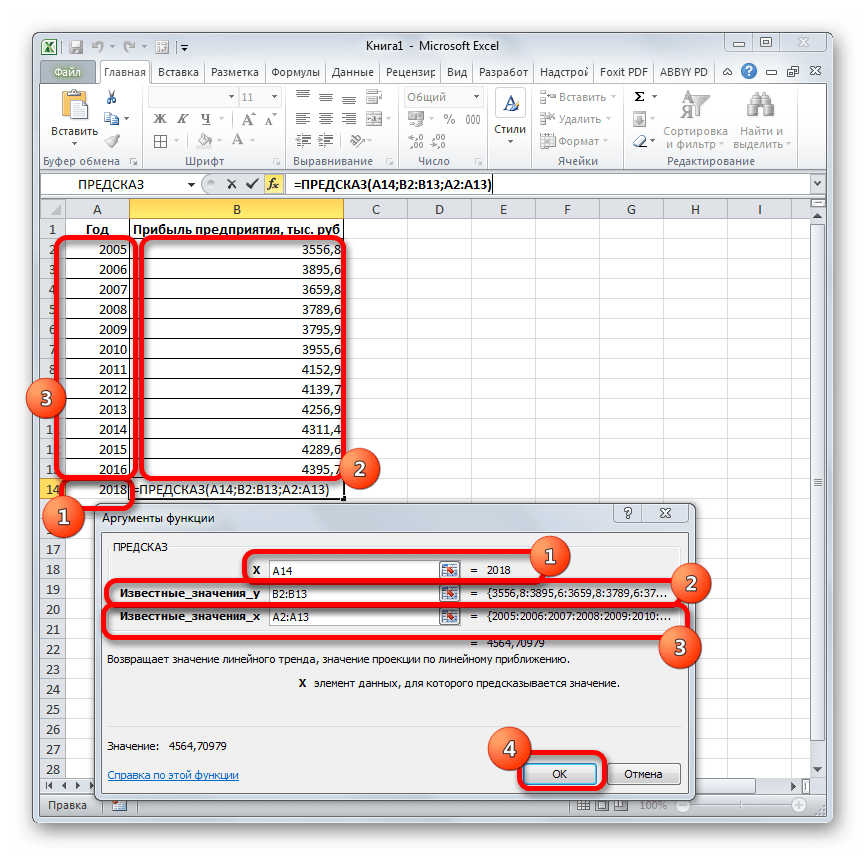
Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.

В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.

Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.

После того, как вся информация внесена, жмем на кнопку «OK».

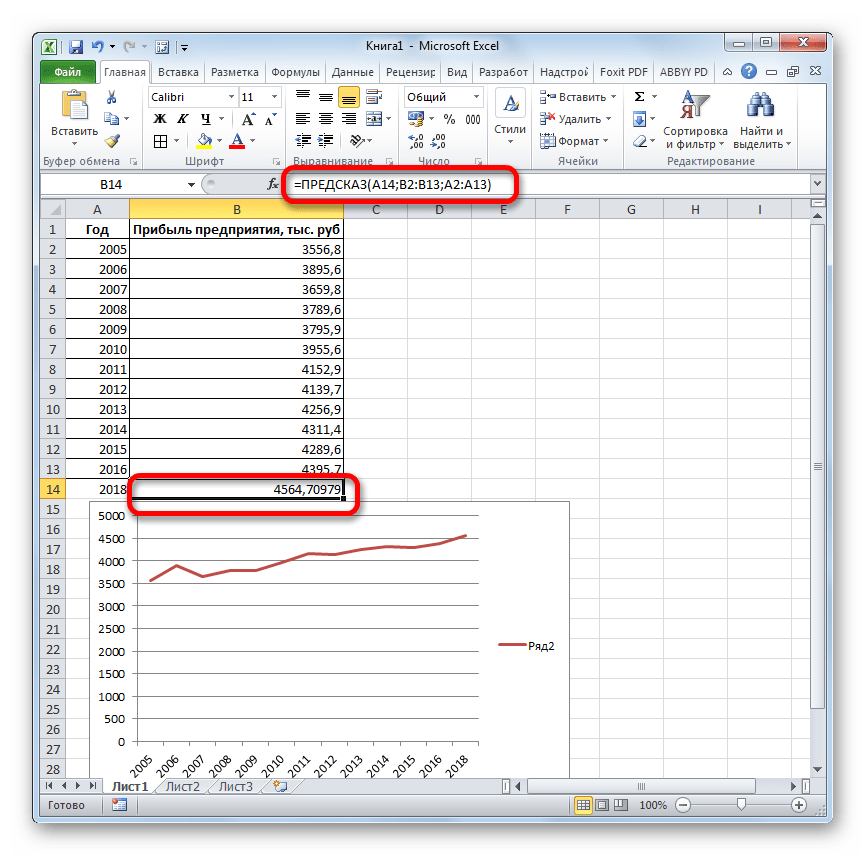
Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.

Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.

Способ 3: оператор ТЕНДЕНЦИЯ

Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:

=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.

Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.

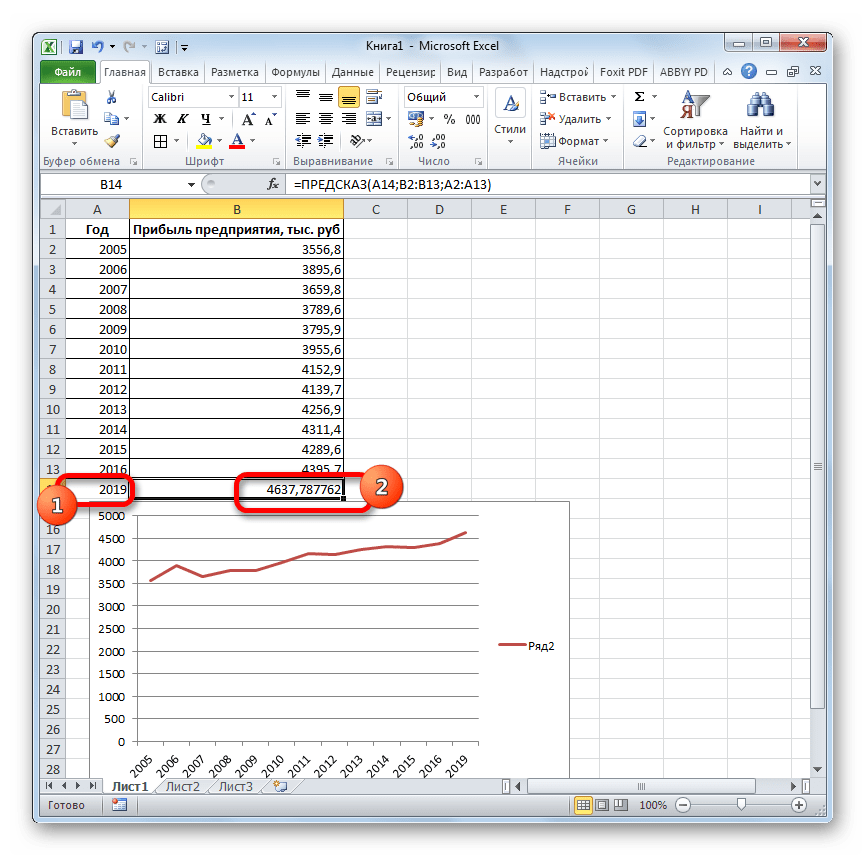
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.

Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».

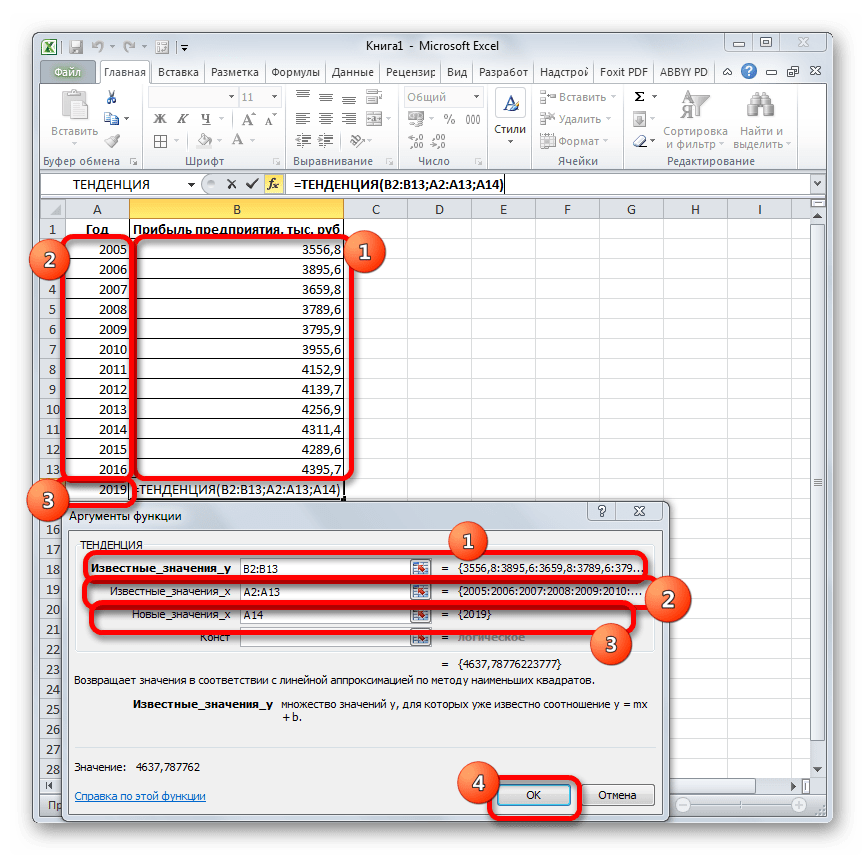
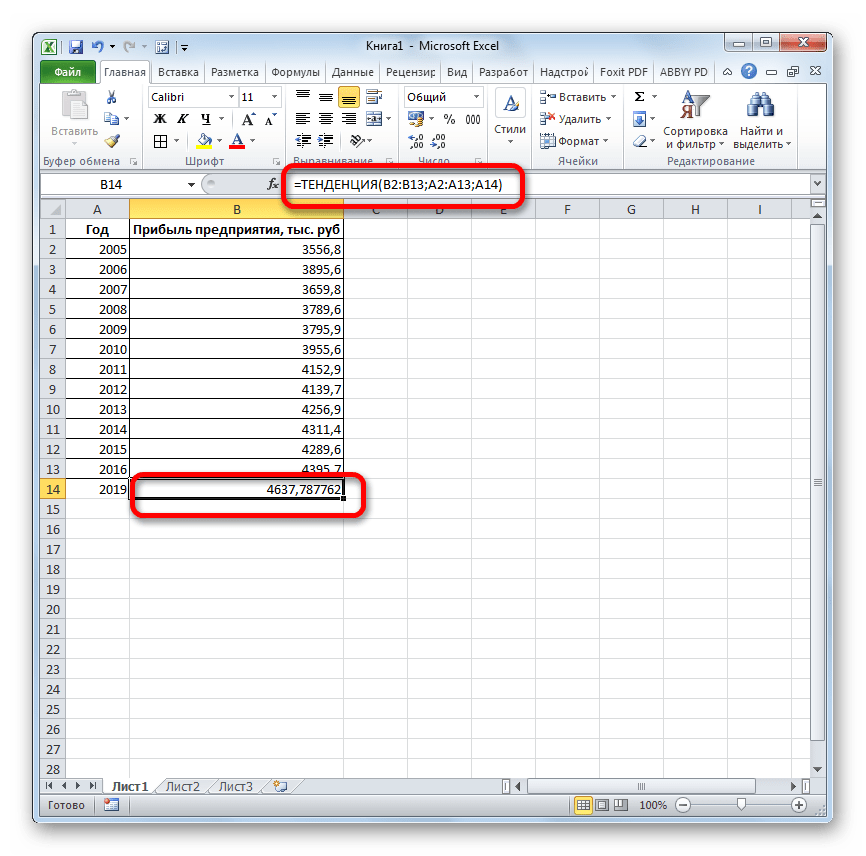
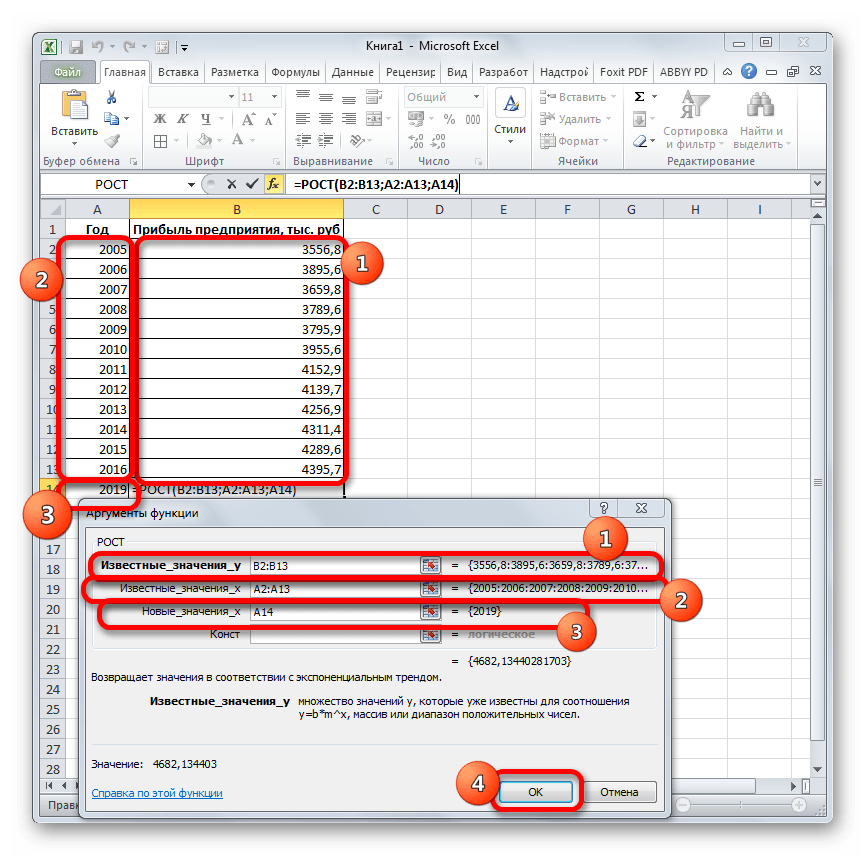
Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».

Способ 4: оператор РОСТ

Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:

=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.

Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».

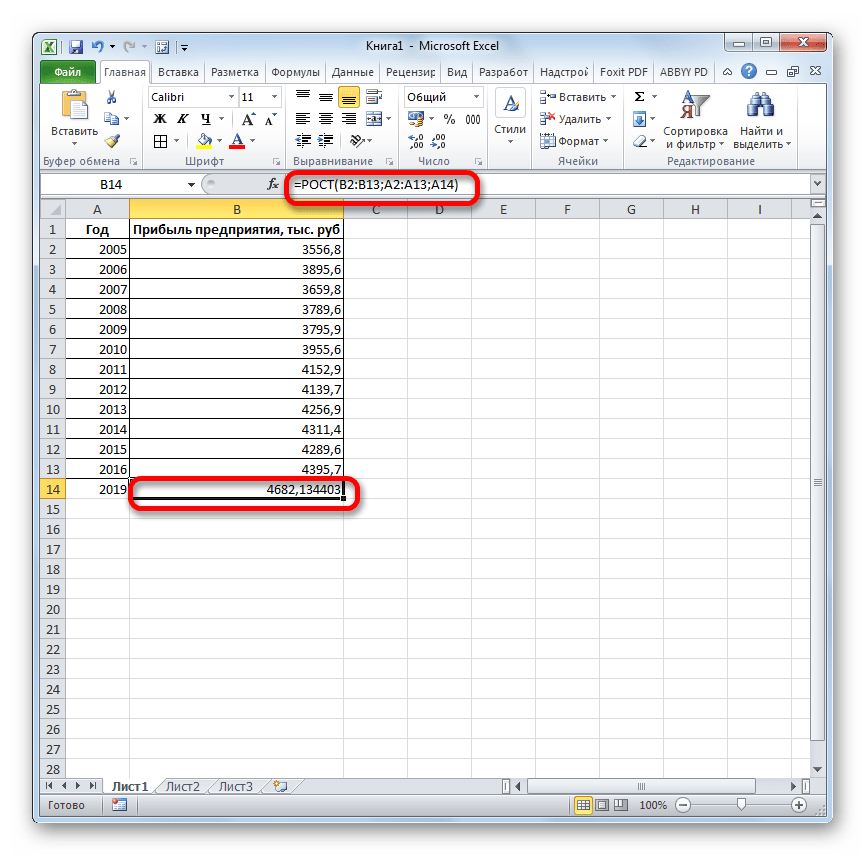
Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».

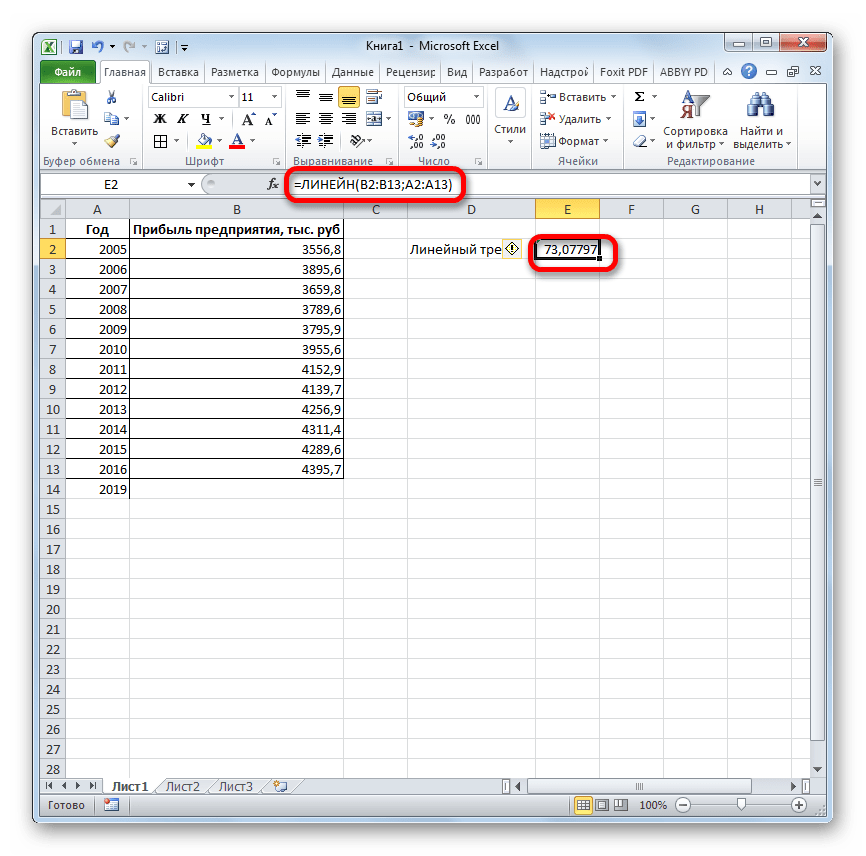
Способ 5: оператор ЛИНЕЙН

Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

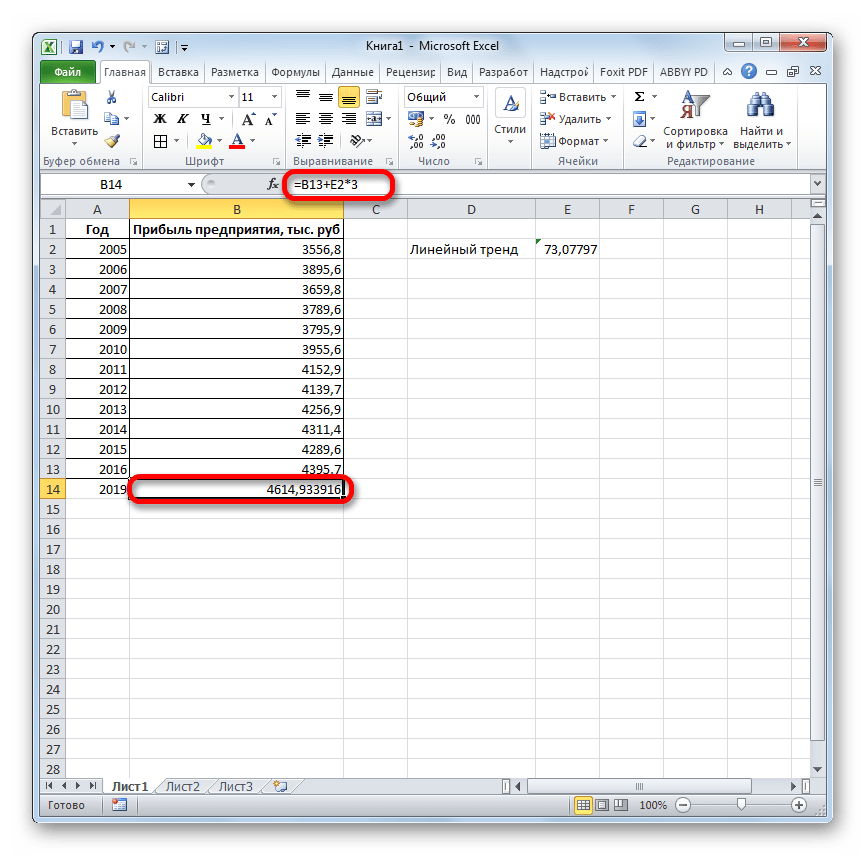
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.

Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».

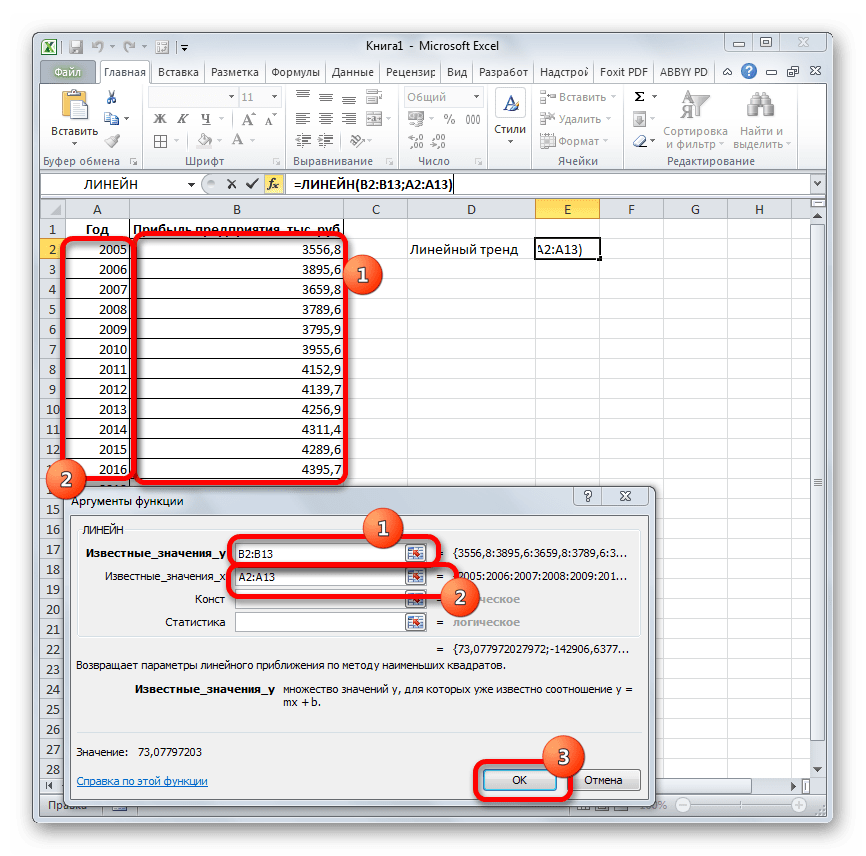
В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».

Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.

Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.

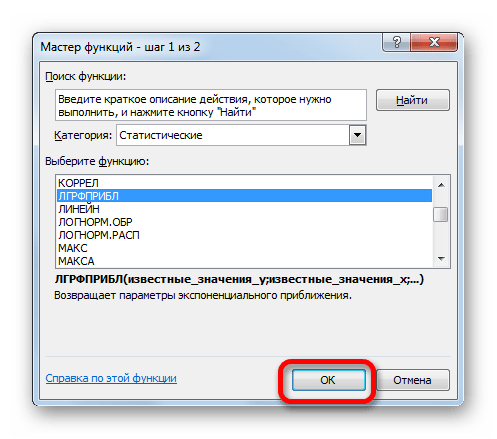
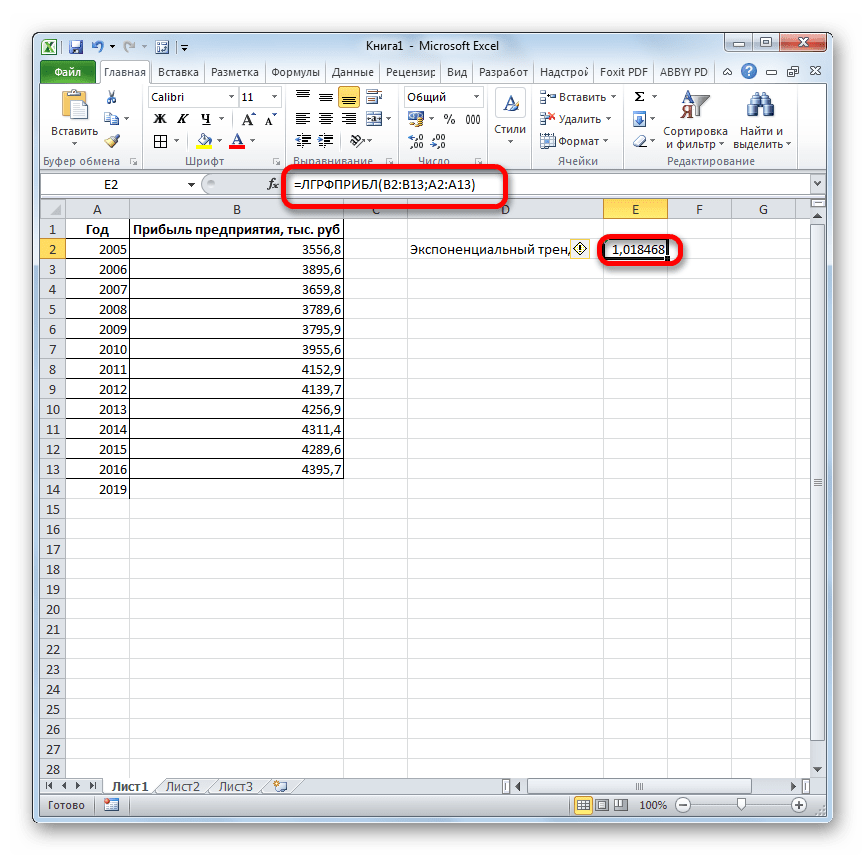
Способ 6: оператор ЛГРФПРИБЛ

Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:

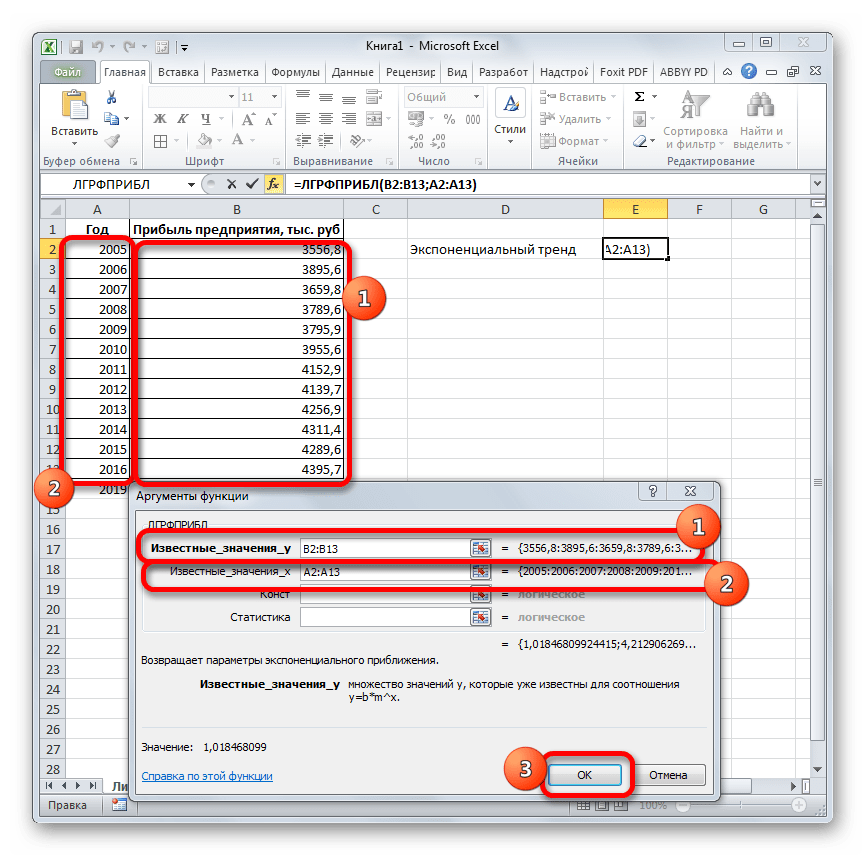
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

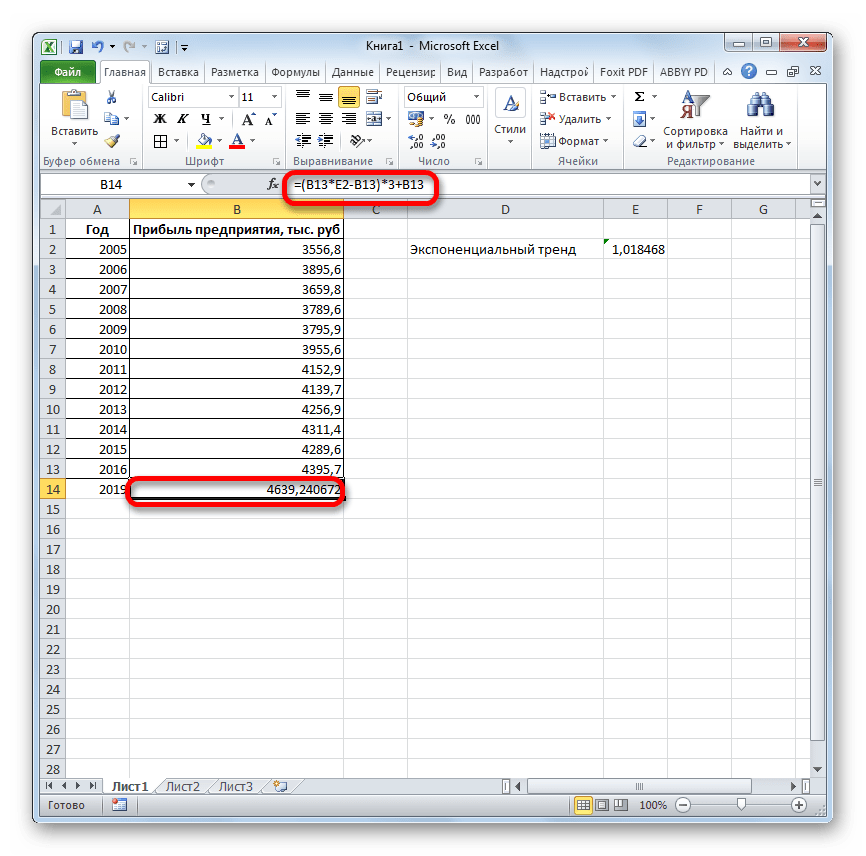
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.

В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».

Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».

Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.

Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.

Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Помимо этой статьи, на сайте еще 12686 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

,

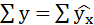
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмиро­вание степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наи­меньших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 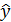. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz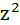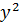
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.