Выражения и уравнения — определение и вычисление с примерами решения
Содержание:
Выражения и уравнения
Вы уже знаете, что такое буквенные выражения, и умеете их упрощать с помощью законов сложения и умножения. Например,
Пример:
Есть ли коэффициент в выражении 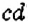
Вспомним, что преобразование выражения со скобками в выражение без скобок называется раскрытием скобок. Например:
Обратным действием в этом примере является вынесение общего множителя за скобки.
Слагаемые, содержащие одинаковые буквенные множители, называют подобными слагаемыми. С помощью вынесения общего множителя за скобки сводят подобные слагаемые:
Правила раскрытия скобок
Правила раскрытия скобок
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках сохраняют;
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
Пример:
Упростите выражение: 1) 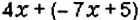
Решение:
1. Перед скобками стоит знак 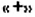
2. Перед скобками стоит знак 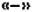
Для раскрытия скобок используют распределительное свойство умножения: 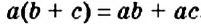
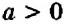
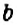
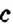
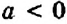
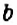
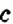
Пример:
Упростите выражение: 1) 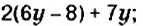
Решение:
1. Множитель 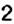
2. Множитель 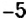
- Слово «сумма» происходит от латинского summа, что значит «итог», «общее количество».
- Слово «плюс» происходит от латинского plus, что значит «больше», а слово «минус» — от латинского minus, что значит «меньше». Знаки
и
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
Уравнения. Основные свойства уравнений
Вы уже знаете, что такое уравнение, корень уравнения. Вспомним основные формулировки.
Определение:
Уравнением называется равенство, содержащее неизвестное, значение которого нужно найти.
Неизвестное число в уравнении обозначают буквой 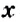
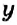
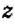
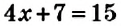
уравнением, где 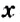
Определение:
Значение неизвестного, обращающее уравнение в верное числовое равенство, называется корнем уравнения.
Так, корнем уравнения 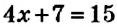
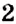
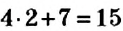
Уравнение может иметь больше одного корня. Например, уравнение 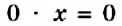
Уравнение может не иметь корней. Например, уравнение 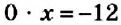
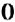
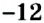
Определение:
Решить уравнение — значит найти все его корни или установить, что уравнение не имеет ни одного корня.
В 5 классе вы находили корень уравнения как неизвестный компонент арифметического действия. При решении более сложных уравнений опираются на свойства равенств. Рассмотрим основные из них.
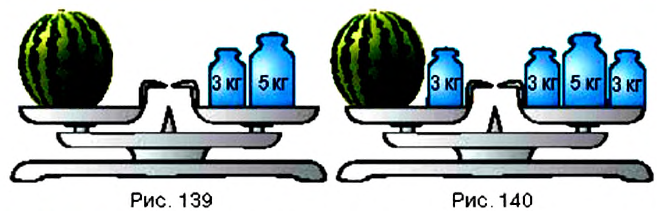
Посмотрите на рисунок 139. Вы видите, что на левой чаше весов находится арбуз неизвестной массы, а на правой — гири массой 5 кг и 3 кг. Если на обе чаши весов положить по гире массой 3 кг, то весы останутся в равновесии (рис. 140). Понятно, что, сняв эти гири или поставив навесы одинаковые гири другой массы, снова получим равновесие на весах. Этот пример иллюстрирует следующее свойство равенств.
Определение: Если к обеим частям равенства прибавить (из обеих частей равенства вычесть) одно и то же число, то равенство не изменится.
Пример:
Решите уравнение: 1) 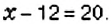
Решение:
К левой и правой частям уравнения прибавим число 12 и упростим полученное равенство:
Решая уравнение, в левой его части «уединили неизвестное». Такой же результат получим, если число 12 перенесём из левой части в правую, изменив при этом его знак.
Определение:
Слагаемое можно переносить из одной части уравнения в другую, изменяя знак этого слагаемого на противоположный.
Пример:
Можно ли переносить в другую часть уравнения слагаемое, содержащее неизвестное? Да.
Посмотрите на рисунок 141. Вы видите, что масса пакета муки равна 2 кг. Понятно, что масса трёх таких пакетов втрое больше (рис. 142). Этот пример иллюстрирует другое свойство равенств.
Определение: Если обе части равенства умножить (разделить) на одно и то же число, отличное от нуля, то равенство не изменится. 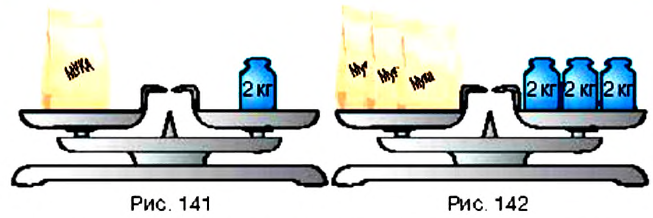
Пример:
Решите уравнение
Решение:
Чтобы избавиться от дробного коэффициента, умножим на 3 обе части уравнения:
Основные свойства уравнений
Основные свойства уравнений
- Корни уравнения не изменятся, если к обеим частям уравнения прибавить (из обеих частей уравнения вычесть) одно и то же число.
- Корни уравнения не изменятся, если обе части уравнения умножить (разделить) на одно и то же число, отличное от нуля.
Считают, что язык алгебры — это уравнения. «Чтобы решить вопросы. относящиеся к числам или к абстрактным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий И. Ньютон (1643-1727) в своём учебнике по алгебре, названном «Общая арифметика».
Применение уравнений к решению задач
В 5 классе с помощью уравнений вы решали задачи на нахождение суммы двух величин или их разности.
В 6 классе будем рассматривать особый вид задач — на равенство двух величин. В таких задачах тоже сравнивают две величины, например, количество книг на первой и второй полках. Значения же выражений с этими двумя величинами приравнивают.
Пример:
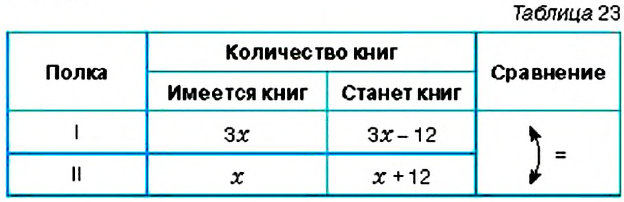
На первой полке книг в 3 раза больше, чем на второй. Если с первой полки переставить на вторую 12 книг, то на обеих полках их станет поровну. Сколько книг на каждой полке?
Решение:
Составим краткую запись задачи в виде таблицы 23
Пусть 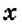
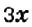
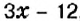
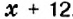
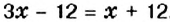
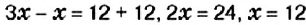

Первым произведением, содержащим исследование алгебраических вопросов, считают трактат «Арифметика» Диофанта (середина IV в.). Из 13 книг, составляющих полное собрание трудов Диофанта, до нас дошло только 6. В них предложено решение сложных алгебраических задач. Основная часть трактата — сборник задач (в первых шести книгах их 189) с решениями и удачно подобранными иллюстрациями к способам решения.
Перпендикулярные и параллельные прямые
Вы знаете, что прямая — это геометрическая фигура. Две прямые могут по-разному размещаться на плоскости. В 6 классе вы узнаете о перпендикулярных и параллельных прямых.
Перпендикулярные прямые
Посмотрите па перекрёсток дорог на рисунке 143. Вы видите, что дороги напоминают пересекающиеся прямые, которые образуют четыре прямых угла. В этом случае говорят, что прямые пересекаются под прямым углом. В тетради по математике клеточки образуются перпендикулярными прямыми.
Определение:
Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым углом.
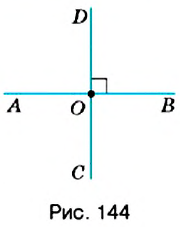
На рисунке 144 изображены прямые 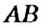
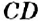

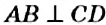
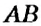
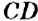
Если прямая 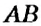
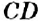

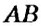
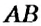
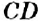
Пример:
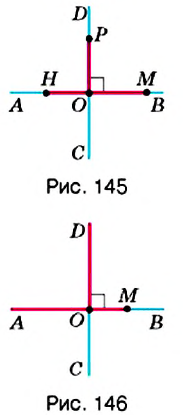
Бывают ли перпендикулярными отрезки? лучи? Да, если они являются частями соответствующих перпендикулярных прямых (рис. 145—146).
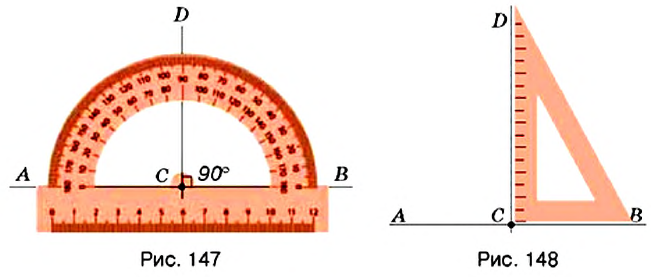
Для построения перпендикулярных прямых используют транспортир или угольник. На рисунке 147 вы видите, как строили прямую 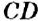

Параллельные прямые
Посмотрите на рисунок 149. Вы видите рельсы трамвайных путей, напоминающие прямые, которые лежат в одной плоскости и не пересекаются. Это пример параллельных прямых. Вокруг нас много других примеров параллельных прямых. Так, в тетради в клеточку горизонтальные линии параллельны. То же самое можно сказать и про вертикальные линии. Противоположные края парты, противоположные стороны оконной рамы, троллейбусные штанги также параллельны.
Определение:
Две прямые на плоскости называются параллельными, если они не пересекаются.
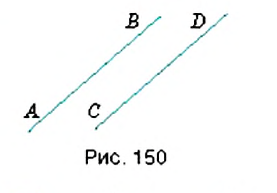
На рисунке 150 изображены параллельные прямые 


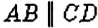


Если прямая 



Пример:
Бывают ли параллельными лучи? отрезки? Да, если они являются частями соответствующих параллельных прямых.
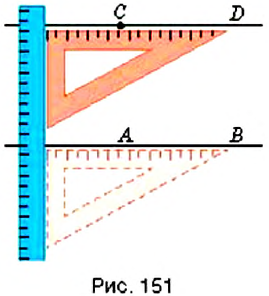
На рисунке 151 вы видите, как с помощью линейки и угольника через точку 


Название «перпендикулярный» происходит от латинского слова «perpendicufaris», которое означает «отвесный». Знак 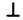
Название «параллельный» происходит от греческого слова «раralelos» — «идущий рядом». Символ параллельности 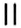
Координатная плоскость
Вы уже знаете, что такое координатная прямая (рис. 162). На ней точка 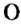
Однако на практике часто приходится пользоваться ориентирами не только вдоль прямой, но и на плоскости.
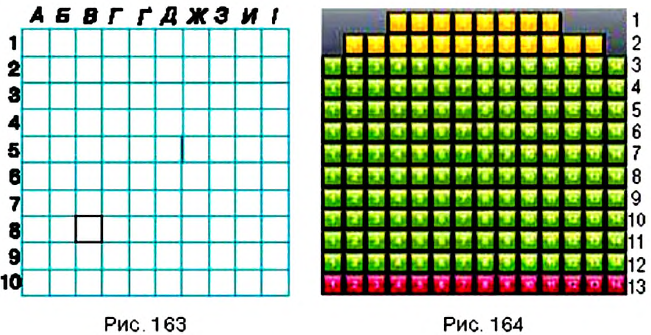
Вы знаете, что в игре «Морской бой» положение корабля определяют с помощью «координат» из цифр и «координат» из букв (рис. 163). В зависимости от выбранной буквы передвигаются на определённое количество клеточек вправо или влево, а цифра указывает, на сколько клеточек нужно сместиться вверх или вниз. Итак, место корабля на поле боя определяют двумя « координатами».
Чтобы определить место в зале кинотеатра, также нужно знать две «координаты»: номер ряда и номер кресла в этом ряду (рис. 164). Причём порядок «координат» в такой паре является строго определённым. Действительно, например, пары чисел 3 и 12 и 12 и 3 направят нас в совершенно разные места зала: в 3-й ряд на 12-е место или в 12-й ряд на 3-е место. В отличие от предыдущего примера, для ориентирования в зале кинотеатра порядок координат не меняют, поскольку неудобно сначала искать номер места в ряду, а лишь затем — сам ряд.
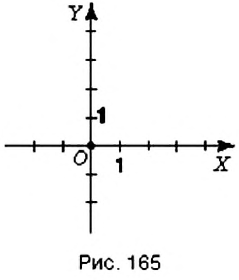
Итак, чтобы охарактеризовать размещение точки на плоскости, нужно задать две координатные прямые с равными единичными отрезками, одна из которых задаёт направление вправо-влево, а вторая — вверх-вниз. Для этого координатные прямые изображают перпендикулярно друг к другу и так, чтобы начала отсчёта на них совпадали (рис. 165). Одну из этих прямых (как правило, горизонтальную) считают первой, а другую — второй. Такая пара координатных прямых образует прямоугольную систему координат.
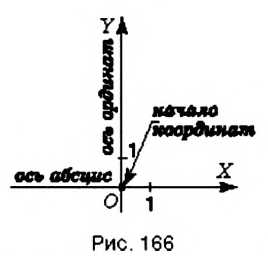
Первую координатную прямую называют осью абсцисс. Её обозначают 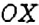
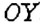
Плоскость с заданной на ней системой координат называют координатной плоскостью.
Каждой точке на плоскости можно поставить в соответствие пару чисел, взятых в определённом порядке, и наоборот, каждой паре чисел соответствует единственная точка координатной плоскости. Такая упорядоченная пара чисел называется координатами точки в данной системе координат. Координату по оси абсцисс называется абсциссой точки, а координату по оси ординат — ординатой точки.

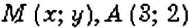
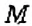
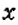
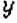
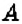
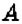
Пример:
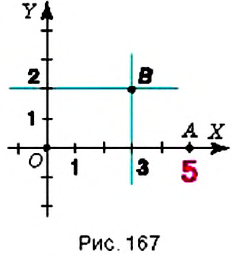
На координатной плоскости постройте точку: 1) 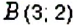
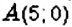
Решение:
Введём прямоугольную систему координат на плоскости (рис. 167).
1. У точки 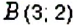
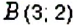
2. Поскольку ордината точки 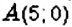
Обратите внимание:
- точка лежит на оси абсцисс, если её ордината равна нулю, и наоборот;
- точка лежит на оси ординат, если её абсцисса равна нулю, и наоборот;
- начало координат — точка
, имеет координаты
.
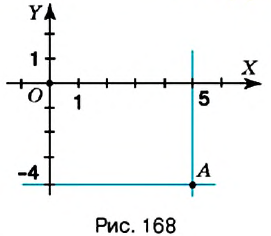
Пример:
Как определить координаты точки, построенной на координатной плоскости, например, точки 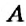
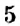
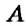
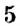
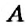
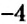
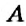
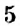
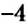
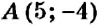
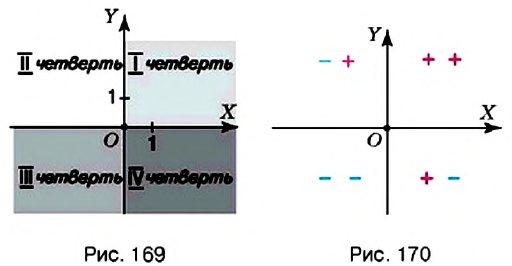
Координатные оси разбивают координатную плоскость на четыре части. Их называют координатными четвертями и обозначают так: I четверть, II четверть, III четверть, IV четверть (рис. 169).
Точки I четверти имеют положительную абсциссу и положительную ординату. И наоборот, если абсцисса и ордината точки положительные, то она лежит в I четверти, как, например, точка 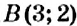
На рисунке 170 показаны знаки координат точек, лежащих в соответствующих четвертях.
Положение любой точки на поверхности Земли определяется двумя координатами: географической широтой и географической долготой.
Географические координаты ввёл древнегреческий учёный Гиппарх во И в. до н.э. Географические координаты применяют для определения положения точек земной поверхности относительно экватора и начального (нулевого) меридиана. Например, Киев имеет следующие географические координаты: 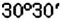
Графики зависимостей между величинами
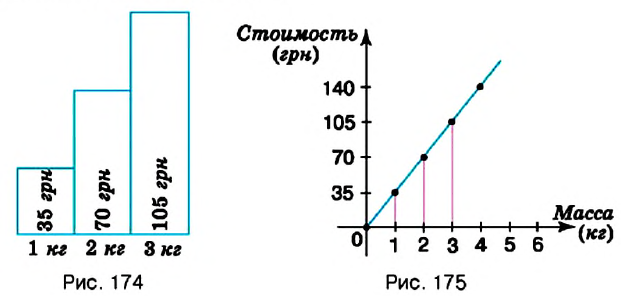
Вы знаете, что стоимость товара зависит от его количества: чем большее количество товара покупают, тем большей будет его стоимость. Например, если цена одного килограмма конфет составляет 35 грн, то за 2 кг нужно заплатить 70 грн, за 3 кг — 105 грн и т.п. Вы знаете, что такое соответствие можно наглядно отобразить на диаграмме (рис. 174). Однако по диаграмме трудно определить, сколько стоит 2,5 кг конфет или иное их количество. Изобразим данные о стоимости конфет не в виде столбиков, а вертикальными отрезками в системе координат (рис. 175). Поскольку величины «масса конфет» и «стоимость покупки» являются прямо пропорциональными, то верхние концы столбиков диаграммы можно соединить отрезками. Получим линию, показывающую, как изменяется стоимость покупки в зависимости от массы конфет. Такая линия называется графиком зависимости величины «стоимость покупки» от величины «масса конфет».
Обратите внимание:
все точки графика зависимости прямо пропорциональных величин лежат на одной прямой.
Вы знаете, что расстояние и время на его преодоление являются прямо пропорциональными величинами. Поэтому все точки графика движения лежат на одной прямой.
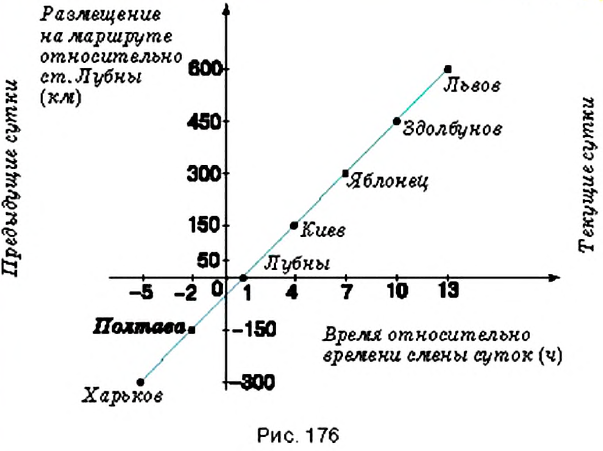
Пример:
Поезд Харьков — Львов выходит из Харькова около 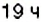
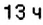
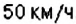
1) В котором часу новых суток поезд делает первую остановку? Какая это станция?
2) Что показывает число 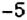
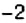
3) На каких расстояниях от первой остановки поезд останавливается на других станциях?
4) Что показывает число 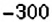
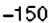
5) Каковы координаты конечных точек маршрута?
Решение:
По условию задачи, движение поезда начинается в 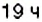
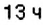
1. Начало новых суток поезд встречает недалеко от станции Лубны, а первую остановку делает в 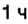
2. Поскольку движение поезда началось в предыдущие сутки, то по оси абсцисс время его отправления из Харькова можно выразить отрицательным числом 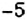
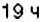
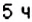
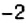
3. Остановки запланированы через каждые 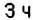
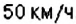
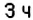
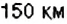
4. При помощи отрицательных чисел 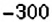
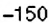
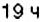
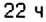
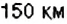
5. Конечные результаты точки маршрута поезда имеют координаты 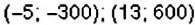
Пример:
Обязательно ли выбирать конечные точки маршрута для построения графика движения? Нет. График можно построить по любым двум его точкам. Но концы маршрута нужно отметить обязательно.
Обратите внимание:
график движения является прямой (или её частью), поэтому такой график можно построить по любым двум его точкам.
С помощью графиков можно решать целый класс задач. Рассмотрим задачу.
Пример:
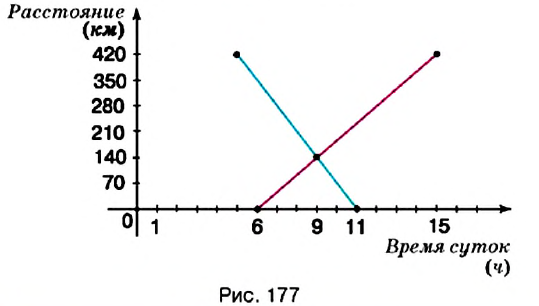
Из пунктов 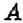
Решение:
Построим в прямоугольной системе координат графики движения автомобилей (рис. 177). Красный отрезок — график движения красного автомобиля, синий — синего автомобиля. Точке пересечения этих отрезков соответствует время — 9 ч. Итак, автомобили встречаются в 9 ч.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Многочлены
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
- Делимость натуральных чисел
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Нахождение значения выражения: правила, примеры, решения
В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.
Как найти значение числового выражения?
Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.
Простейшие случаи
Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.
Если в выражении есть только числа и арифметические знаки » + » , » · » , » — » , » ÷ » , то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.
Пример 1. Значение числового выражения
Пусть нужно найти значения выражения 14 — 2 · 15 ÷ 6 — 3 .
Выполним сначала умножение и деление. Получаем:
14 — 2 · 15 ÷ 6 — 3 = 14 — 30 ÷ 6 — 3 = 14 — 5 — 3 .
Теперь проводим вычитание и получаем окончательный результат:
14 — 5 — 3 = 9 — 3 = 6 .
Вычислим: 0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 .
Сначала выполняем преобразование дробей, деление и умножение:
0 , 5 — 2 · — 7 + 2 3 ÷ 2 3 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12
1 2 — ( — 14 ) + 2 3 ÷ 11 4 · 11 12 = 1 2 — ( — 14 ) + 2 3 · 4 11 · 11 12 = 1 2 — ( — 14 ) + 2 9 .
Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:
1 2 — ( — 14 ) + 2 9 = 1 2 + 14 + 2 9 = 14 + 13 18 = 14 13 18 .
Искомое значение найдено.
Выражения со скобками
Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.
Пример 3. Значение числового выражения
Найдем значение выражения 0 , 5 · ( 0 , 76 — 0 , 06 ) .
В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.
0 , 5 · ( 0 , 76 — 0 , 06 ) = 0 , 5 · 0 , 7 = 0 , 35 .
Значение выражений, содержащих скобки в скобках, находится по такому же принципу.
Пример 4. Значение числового выражения
Вычислим значение 1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 .
Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.
1 + 2 · 1 + 2 · 1 + 2 · 1 — 1 4 = 1 + 2 · 1 + 2 · 1 + 2 · 3 4
1 + 2 · 1 + 2 · 1 + 2 · 3 4 = 1 + 2 · 1 + 2 · 2 , 5 = 1 + 2 · 6 = 13 .
В нахождении значений выражений со скобками главное — соблюдать последовательность действий.
Выражения с корнями
Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.
Пример 5. Значение числового выражения
Вычислим значение выражения с корнями — 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 .
Сначала вычисляем подкоренные выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 = — 6 — 1 + 15 3 = 8 3 = 2
2 , 2 + 0 , 1 · 0 , 5 = 2 , 2 + 0 , 05 = 2 , 25 = 1 , 5 .
Теперь можно вычислить значение всего выражения.
— 2 · 3 — 1 + 60 ÷ 4 3 + 3 · 2 , 2 + 0 , 1 · 0 , 5 = 2 + 3 · 1 , 5 = 6 , 5
Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.
Пример 6. Значение числового выражения
Сколько будет 3 + 1 3 — 1 — 1
Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.
3 + 1 3 — 1 = 3 — 1 .
3 + 1 3 — 1 — 1 = 3 — 1 — 1 = 1 .
Выражения со степенями
Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.
Пример 7. Значение числового выражения
Найдем значение выражения 2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 .
Начинаем вычислять по порядку.
2 3 · 4 — 10 = 2 12 — 10 = 2 2 = 4
16 · 1 — 1 2 3 , 5 — 2 · 1 4 = 16 * 0 , 5 3 = 16 · 1 8 = 2 .
Осталось только провести операцию сложение и узнать значение выражения:
2 3 · 4 — 10 + 16 1 — 1 2 3 , 5 — 2 · 1 4 = 4 + 2 = 6 .
Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.
Пример 8. Значение числового выражения
Вычислим значение следующего выражения: 2 — 2 5 · 4 5 — 1 + 3 1 3 6 .
Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.
2 — 2 5 · 4 5 — 1 + 3 1 3 6 = 2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6
2 — 2 5 · 2 2 5 — 1 + 3 1 3 · 6 = 2 — 2 5 · 2 2 · 5 — 2 + 3 2 = 2 2 · 5 — 2 — 2 5 + 3 2
2 2 · 5 — 2 — 2 5 + 3 2 = 2 — 2 + 3 = 1 4 + 3 = 3 1 4
Выражения с дробями
Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.
Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.
Пример 9. Значение числового выражения
Найдем значение выражения, содержащего дроби: 3 , 2 2 — 3 · 7 — 2 · 3 6 ÷ 1 + 2 + 3 9 — 6 ÷ 2 .
Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.
3 , 2 2 = 3 , 2 ÷ 2 = 1 , 6
7 — 2 · 3 6 = 7 — 6 6 = 1 6
1 + 2 + 3 9 — 6 ÷ 2 = 1 + 2 + 3 9 — 3 = 6 6 = 1 .
Перепишем наше выражение и вычислим его значение:
1 , 6 — 3 · 1 6 ÷ 1 = 1 , 6 — 0 , 5 ÷ 1 = 1 , 1
Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.
Пример 10. Значение числового выражения
Вычислим выражение 2 5 — 1 — 2 5 — 7 4 — 3 .
Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.
2 5 — 1 = 2 5 + 1 5 — 1 5 + 1 = 2 5 + 1 5 — 1 = 2 5 + 2 4
Исходное выражение принимает вид:
2 5 — 1 — 2 5 — 7 4 — 3 = 2 5 + 2 4 — 2 5 — 7 4 — 3 .
Вычислим значение этого выражения:
2 5 + 2 4 — 2 5 — 7 4 — 3 = 2 5 + 2 — 2 5 + 7 4 — 3 = 9 4 — 3 = — 3 4 .
Выражения с логарифмами
Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log 2 4 + 2 · 4 можно сразу вместо log 2 4 записать значение этого логарифма, а потом выполнить все действия. Получим: log 2 4 + 2 · 4 = 2 + 2 · 4 = 2 + 8 = 10 .
Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log 5 — 6 ÷ 3 5 2 + 2 + 7 . Имеем:
log 5 — 6 ÷ 3 5 2 + 2 + 7 = log 3 27 + 7 = 3 + 7 = 10 .
Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.
Пример 11. Значение числового выражения
Найдем значение выражения log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 .
log 2 log 2 256 = log 2 8 = 3 .
По свойству логарифмов:
log 6 2 + log 6 3 = log 6 ( 2 · 3 ) = log 6 6 = 1 .
Вновь применяя свойства логарифмов, для последней дроби в выражении получим:
log 5 729 log 0 , 2 27 = log 5 729 log 1 5 27 = log 5 729 — log 5 27 = — log 27 729 = — log 27 27 2 = — 2 .
Теперь можно переходить к вычислению значения исходного выражения.
log 2 log 2 256 + log 6 2 + log 6 3 + log 5 729 log 0 , 2 27 = 3 + 1 + — 2 = 2 .
Выражения с тригонометрическими функциями
Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.
Пример 12. Значение числового выражения
Найдите значение выражения: t g 2 4 π 3 — sin — 5 π 2 + cosπ .
Сначала вычисляем значения тригонометрических функций, входящих в выражение.
Подставляем значения в выражение и вычисляем его значение:
t g 2 4 π 3 — sin — 5 π 2 + cosπ = 3 2 — ( — 1 ) + ( — 1 ) = 3 + 1 — 1 = 3 .
Значение выражения найдено.
Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.
Пример 13. Значение числового выражения
Нужно найти значение выражения cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 .
Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.
cos 2 π 8 — sin 2 π 8 cos 5 π 36 cos π 9 — sin 5 π 36 sin π 9 — 1 = cos 2 π 8 cos 5 π 36 + π 9 — 1 = cos π 4 cos π 4 — 1 = 1 — 1 = 0 .
Общий случай числового выражения
В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.
Как найти значение выражения
- Корни, степени, логарифмы и т.д. заменяются их значениями.
- Выполняются действия в скобках.
- Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.
Пример 14. Значение числового выражения
Вычислим, чему равно значение выражения — 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 .
Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?
Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.
Первым делом вычислим значение подкоренного выражения 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 . Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.
π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π
Теперь можно узнать значение синуса:
sin π 6 + 2 · 2 π 5 + 3 π 5 = sin π 6 + 2 π = sin π 6 = 1 2 .
Вычисляем значение подкоренного выражения:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 4 = 2 .
Со знаменателем дроби все проще:
Теперь мы можем записать значение всей дроби:
2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 = 2 2 = 1 .
С учетом этого, запишем все выражение:
— 1 + 1 + 3 9 = — 1 + 1 + 3 3 = — 1 + 1 + 27 = 27 .
— 2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 ln e 2 + 1 + 3 9 = 27 .
В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.
Вычисление значений выражений рациональными способами
Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2 · 386 + 5 + 589 4 1 — sin 3 π 4 · 0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.
Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56 + 8 — 3 , 789 ln e 2 — 56 + 8 — 3 , 789 ln e 2 также равно нулю.
Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе.
Например, возьмем выражение 2 3 — 1 5 + 3 · 289 · 3 4 3 · 2 3 — 1 5 + 3 · 289 · 3 4 . Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 1 3 .
Нахождение значений выражений с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.
Нахождение значений выражений с переменными
Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.
Вычислить значение выражения 0 , 5 x — y при заданных x = 2 , 4 и y = 5 .
Подставляем значения переменных в выражение и вычисляем:
0 , 5 x — y = 0 , 5 · 2 , 4 — 5 = 1 , 2 — 5 = — 3 , 8 .
Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.
Например, выражение х + 3 — х , очевидно, имеет значение 3 , и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.
Еще один пример. Значение выражения x x равно единице для всех положительных иксов.
Нахождение значения выражения, примеры, решения.
После того, как мы узнали что такое значение выражения, логичным будет разобраться с вопросом как найти значение выражения. Сейчас мы рассмотрим правила нахождения значений выражений. Начнем с числовых выражений, и будем продвигаться от самых простых случаев, когда выражение содержит лишь числа и соединяющие их знаки арифметических действий, и закончим общим случаем, когда в выражении, значение которого нужно найти, содержатся скобки, дроби, корни, степени и другие функции. В конце покажем, как находить значения буквенных выражений и выражений с переменными при выбранных значениях переменных. Всю теорию снабдим примерами с подробным описанием решений.
Навигация по странице.
Как найти значение числового выражения?
Перевод условий задач на математический язык часто дает числовые выражения, то есть, выражения, составленные из чисел и знаков действий. Они могут быть как очень простыми, состоящими из чисел и знаков арифметических действий, так и достаточно сложными и громоздкими, содержащими скобки, степени, дроби, корни и т.п. Но составленное выражение зачастую является лишь промежуточным этапом решения задачи, а ответ заключается в значении составленного выражения. Так мы приходим к задаче — найти значение выражения.
Разберемся с правилами, по которым вычисляются значения выражений.
Простейшие случаи
Знакомство с правилами нахождения значений выражений начнем со случаев, когда числовое выражение не содержит в своей записи ничего другого, кроме чисел и знаков арифметических действий. Эти случаи мы и назвали простейшими.
Чтобы успешно находить значения таких выражений, нужно уметь выполнять действия с различными числами, а также иметь представление о порядке выполнения действий в выражениях без скобок.
Итак, если числовое выражение составлено из чисел и знаков +, −, · и :, то по порядку слева направо нужно сначала выполнить умножение и деление, а затем – сложение и вычитание, что позволит найти искомое значение выражения.
Приведем решение примеров для пояснения.
Вычислите значение выражения 14−2·15:6−3 .
Чтобы найти значение выражения, нужно выполнить все указанные в нем действия в соответствии с принятым порядком выполнения этих действий. Вначале по порядку слева направо выполняем умножение и деление, получаем 14−2·15:6−3=14−30:6−3=14−5−3 . Теперь также по порядку слева направо выполняем оставшиеся действия: 14−5−3=9−3=6 . Так мы нашли значение исходного выражения, оно равно 6 .
Найдите значение выражения 
В данном примере нам сначала нужно выполнить умножение 2·(−7) и деление с умножением в выражении 




Подставляем полученные значения в исходное выражение: 
Осталось записать десятичную дробь в виде обыкновенной дроби 



Так мы нашли искомое значение выражения.

Со скобками
Теперь разберемся, как найти значение выражения, содержащего в своей записи скобки, указывающие порядок выполнения действий. При этом сначала следует находить значение выражений в скобках, придерживаясь принятого порядка выполнения действий, а затем выполнять остальные действия, что приведет к искомому значению исходного выражения. Это правило перекликается с порядке выполнения действий в выражениях без скобокпорядком выполнения действий в выражениях со скобками.
Покажем решение примера.
Вычислите значение выражения 0,5·(0,75−0,05) .
В данном примере для нахождения значения выражения нам нужно будет выполнять действия с десятичными дробями. Так как исходное выражение содержит скобки, то сначала нужно найти значение выражения в них, имеем 0,5·(0,75−0,05)=0,5·0,7 . Остается выполнить умножение: 0,5·0,7=0,35 .
Аналогично находятся значения выражений, содержащих скобки в скобках. Удобно нахождение значения начинать со внутренних скобок и продвигаться к внешним.
Найдите значение выражения 1+2·(1+2·(1+2·(1−1/4))) .
Во внутренних скобках находится выражение 1−1/4 , его значение равно 3/4 . Подставив его в исходное выражение, оно примет вид 1+2·(1+2·(1+2·3/4)) . Опять вычисляем значение выражения во внутренних скобках, не забывая, что умножение выполняется перед сложением, 1+2·3/4=1+3/2=5/2 , и подставляем это значение в последнее выражение: 1+2·(1+2·5/2) . Остается найти значение выражения в скобках, после чего можно будет закончить вычисления: 1+2·(1+2·5/2)=1+2·6=13 .
Запишем краткое решение:
1+2·(1+2·(1+2·(1−1/4)))= 1+2·(1+2·(1+2·3/4))= 1+2·(1+2·(1+2·3/4))= =1+2·(1+2·5/2)= 1+2·6=13 .
Итак, в нахождении значений выражений со скобками нет ничего сложного, главное – соблюдать последовательность выполнения действий, и не допускать вычислительных ошибок.
С корнями
Числовые выражения, значения которых требуется найти, могут в своей записи содержать различные знаки, в частности, корни. Как найти значение корня, под которым стоит число, объясняет материал статьи извлечение корней.
А как быть, когда под знаком корня находится числовое выражение? Чтобы получить значение такого корня, нужно сначала найти значение подкоренного выражения, придерживаясь принятого порядка выполнений действий. Например, 
В числовых выражениях корни следует воспринимать как некоторые числа, и корни целесообразно сразу заменить их значениями, после чего находить значение полученного выражения без корней, выполняя действия в принятой последовательности.
Найдите значение выражения с корнями 
Сначала найдем значение корня 

Теперь вычислим значение второго корня из исходного выражения: 
Наконец, мы можем найти значение исходного выражения, заменив корни их значениями: 

Достаточно часто, чтобы стало возможно найти значение выражения с корнями, предварительно приходится проводить его преобразование. Покажем решение примера.
Каково значение выражения 
Мы не имеем возможности заменить корень из трех его точным значением, что не позволяет нам вычислить значение этого выражения описанным выше способом. Однако мы можем вычислить значение этого выражение, выполнив несложные преобразования. Применим формулу разности квадратов: 


Со степенями
Когда в выражении, значение которого мы находим, присутствуют степени, то их значения вычисляются до выполнения остальных действий. Вычислению значений степеней чисел посвящена статья возведение в степень.
Если основание и показатель степени являются числами, то их значение вычисляется по определению степени, например, 3 2 =3·3=9 или 8 −1 =1/8 . Встречаются также записи, когда основание и/или показатель степени являются некоторыми выражениями. В этих случаях нужно найти значение выражения в основании, значение выражения в показателе, после чего вычислить значение самой степени.
Найдите значение выражения со степенями вида 2 3·4−10 +16·(1−1/2) 3,5−2·1/4 .
В исходном выражении две степени 2 3·4−10 и (1−1/2) 3,5−2·1/4 . Их значения нужно вычислить до выполнения остальных действий.
Начнем со степени 2 3·4−10 . В ее показателе находится числовое выражение, вычислим его значение: 3·4−10=12−10=2 . Теперь можно найти значение самой степени: 2 3·4−10 =2 2 =4 .
В основании и показателе степени (1−1/2) 3,5−2·1/4 находятся выражения, вычисляем их значения, чтобы потом найти значение степени. Имеем (1−1/2) 3,5−2·1/4 =(1/2) 3 =1/8 .
Теперь возвращаемся к исходному выражению, заменяем в нем степени их значениями, и находим нужное нам значение выражения: 2 3·4−10 +16·(1−1/2) 3,5−2·1/4 = 4+16·1/8=4+2=6 .
2 3·4−10 +16·(1−1/2) 3,5−2·1/4 =6 .
Стоит заметить, что более распространены случаи, когда целесообразно провести предварительное упрощение выражения со степенями на базе свойств степени.
Найдите значение выражения 
Судя по показателям степеней, находящихся в данном выражении, точные значения степеней получить не удастся. Попробуем упростить исходное выражение, может быть это поможет найти его значение. Имеем

Степени в выражениях зачастую идут рука об руку с логарифмами, но о нахождении значений выражений с логарифмами мы поговорим в одном из следующих пунктов.
Находим значение выражения с дробями
Числовые выражения в своей записи могут содержать дроби. Когда требуется найти значение подобного выражения, дроби, отличные от обыкновенных дробей, следует заменить их значениями перед выполнением остальных действий.
В числителе и знаменателе дробей (которые отличны от обыкновенных дробей) могут находиться как некоторые числа, так и выражения. Чтобы вычислить значение такой дроби нужно вычислить значение выражения в числителе, вычислить значение выражения в знаменателе, после чего вычислить значение самой дроби. Такой порядок объясняется тем, что дробь a/b , где a и b – некоторые выражения, по сути представляет собой частное вида (a):(b) , так как черта дроби означает знак деления.
Рассмотрим решение примера.
Найдите значение выражения с дробями 
В исходном числовом выражении три дроби 

В числителе и знаменателе дроби 

В числителе дроби 

Третья дробь 

Осталось подставить найденные значения в исходное выражение, и выполнить оставшиеся действия: 

Часто при нахождении значений выражений с дробями приходится выполнять упрощение дробных выражений, базирующееся на выполнении действий с дробями и на сокращении дробей.
Найдите значение выражения 
Корень из пяти нацело не извлекается, поэтому для нахождения значения исходного выражения для начала упростим его. Для этого избавимся от иррациональности в знаменателе первой дроби: 



С логарифмами
Если числовое выражение содержит логарифмы, и если есть возможность избавиться от них, вычислив значение логарифмов, то это делается перед выполнением остальных действий. Например, при нахождении значения выражения log24+2·3 , логарифм log24 заменяется его значением 2 , после чего выполняются остальные действия в обычном порядке, то есть, log24+2·3=2+2·3=2+6=8 .
Когда под знаком логарифма и/или в его основании находятся числовые выражения, то сначала находятся их значения, после чего вычисляется значение логарифма. Для примера рассмотрим выражение с логарифмом вида 


Если же логарифмы не вычисляются точно, то найти значение исходного выражения может помочь предварительное его упрощение с использованием свойств логарифмов. При этом нужно хорошо владеть материалом статьи преобразование логарифмических выражений.
Найдите значение выражения с логарифмами 
Начнем с вычисления log2(log2256) . Так как 256=2 8 , то log2256=8 , следовательно, log2(log2256)=log28=log22 3 =3 .
Логарифмы log62 и log63 можно сгруппировать. Сумма логарифмов log62+log63 равна логарифму произведения log6(2·3) , таким образом, log62+log63=log6(2·3)=log66=1 .
Теперь разберемся с дробью 

Осталось лишь подставить полученные результаты в исходное выражение и закончить нахождение его значения:

Как найти значение тригонометрического выражения?
Когда числовое выражение содержит синус, косинус, тангенс, котангенс или арксинус, арккосинус, арктангенс, арккотангенс и т.п., то их значения вычисляются перед выполнением остальных действий. Если под знаком тригонометрических функций стоят числовые выражения, то сначала вычисляются их значения, после чего находятся значения тригонометрических функций.
Найдите значение выражения 
Обратившись к статье нахождение значений тригонометрических функций, получаем 



Стоит отметить, что вычисление значений выражений с синусами, косинусами и т.п. зачастую требует предварительного преобразования тригонометрического выражения.
Чему равно значение тригонометрического выражения 
Преобразуем исходное выражение, используя тригонометрические формулы, в данном случае нам потребуются формула косинуса двойного угла и формула косинуса суммы:
Проделанные преобразования помогли нам найти значение выражения.

Общий случай
В общем случае числовое выражение может содержать и корни, и степени, и дроби, и какие-либо функции, и скобки. Нахождение значений таких выражений состоит в выполнении следующих действий:
- сначала корни, степени, дроби и т.п. заменяются их значениями,
- дальше действия в скобках,
- и по порядку слева направо выполняется оставшиеся действия — умножение и деление, а за ними – сложение и вычитание.
Перечисленные действия выполняются до получения конечного результата.
Найдите значение выражения 
Вид данного выражения довольно сложен. В этом выражении мы видим дробь, корни, степени, синус и логарифм. Как же найти его значение?
Продвигаясь по записи слева на право, мы натыкаемся на дробь вида 
В числителе мы имеем корень вида 






Со знаменателем все просто: 
Таким образом, 
После подстановки этого результата в исходное выражение, оно примет вид 


Итак, 

Если же нет возможности вычислить точные значения корней, степеней и т.п., то можно попробовать избавиться от них с помощью каких-либо преобразований, после чего вернуться к вычислению значения по указанной схеме.
Рациональные способы вычисления значений выражений
Вычисление значений числовых выражений требует последовательности и аккуратности. Да, необходимо придерживаться последовательности выполнения действий, записанной в предыдущих пунктах, но не нужно это делать слепо и механически. Этим мы хотим сказать, что часто можно рационализировать процесс нахождения значения выражения. Например, значительно ускорить и упростить нахождение значения выражения позволяют некоторые свойства действий с числами.
К примеру, мы знаем такое свойство умножения: если один из множителей в произведении равен нулю, то и значение произведения равно нулю. Используя это свойство, мы можем сразу сказать, что значение выражения 0·(2·3+893−3234:54·65−79·56·2,2)· (45·36−2·4+456:3·43) равно нулю. Если бы мы придерживались стандартного порядка выполнения действий, то сначала нам бы пришлось вычислять значения громоздких выражений в скобках, а это бы заняло массу времени, и в результате все равно получился бы нуль.
Также удобно пользоваться свойством вычитания равных чисел: если от числа отнять равное ему число, то в результате получится нуль. Это свойство можно рассматривать шире: разность двух одинаковых числовых выражений равна нулю. Например, не вычисляя значения выражений в скобках можно найти значение выражения (54·6−12·47362:3)−(54·6−12·47362:3) , оно равно нулю, так как исходное выражение представляет собой разность одинаковых выражений.
Рациональному вычислению значений выражений могут способствовать тождественные преобразования. Например, бывает полезна группировка слагаемых и множителей, не менее часто используется вынесение общего множителя за скобки. Так значение выражения 53·5+53·7−53·11+5 очень легко находится после вынесения множителя 53 за скобки: 53·(5+7−11)+5=53·1+5=53+5=58 . Непосредственное вычисление заняло бы намного больше времени.
В заключение этого пункта обратим внимание на рациональный подход к вычислению значений выражений с дробями – одинаковые множители в числителе и знаменателе дроби сокращаются. Например, сокращение одинаковых выражений в числителе и знаменателе дроби 
Нахождение значения буквенного выражения и выражения с переменными
Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных. То есть, речь идет о нахождении значения буквенного выражения для данных значений букв или о нахождении значения выражения с переменными для выбранных значений переменных.
Правило нахождения значения буквенного выражения или выражения с переменными для данных значений букв или выбранных значений переменных таково: в исходное выражение нужно подставить данные значения букв или переменных, и вычислить значение полученного числового выражения, оно и является искомым значением.
Вычислите значение выражения 0,5·x−y при x=2,4 и y=5 .
http://zaochnik.com/spravochnik/matematika/vyrazhenija/nahozhdenie-znachenija-vyrazhenija/
http://www.cleverstudents.ru/expressions/finding_value_of_expression.html
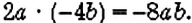
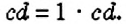
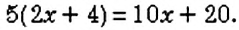
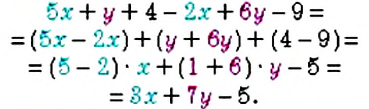
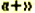 , то при раскрытии скобок знаки слагаемых в скобках сохраняют;
, то при раскрытии скобок знаки слагаемых в скобках сохраняют; , то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.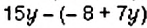
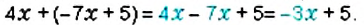
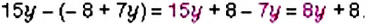
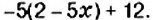
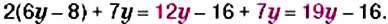
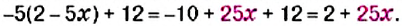
 и
и  используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
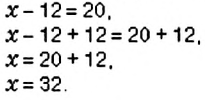
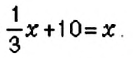
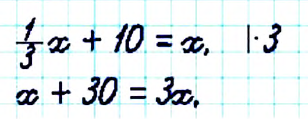
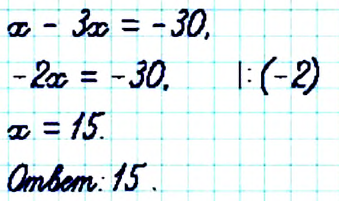




 , имеет координаты
, имеет координаты 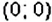 .
.