Как не потерять решение в дифференциальных уравнениях

Немного о потере решений в дифференциальных уравнениях

В однородных уравнениях решение может потеряться в результате типовой замены и дальнейших сокращений, однако, на практике распространена и другая причина потери решений – это неосмотрительное деление. На самом деле с этим мы столкнулись в первом же примере вводного урока о дифференциальных уравнениях. В процессе решения уравнения «игрек» оказался в знаменателе: , но , очевидно, является решением ДУ и в результате неравносильного преобразования (деления) есть все шансы его потерять! Другое дело, что оно вошло в общее решение при нулевом значении константы.

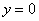
Аналогичная история с уравнением Примера 3 того же урока, в ходе решения которого мы «сбросили» в знаменатель. Строго говоря, следовало предварительно проверить, а не является ли решением данного диффура. Ведь является! Но и тут «всё обошлось», поскольку эта функция вошла в общий интеграл при нулевом значении константы.

В действительности, конечно же, вовсе «не обошлось» – ситуация была под контролем, но я намеренно умолчал об этих нюансах на 1-ом уроке, чтобы не перегружать «чайников» информацией.

При неравносильных преобразованиях ВСЕГДА проверяйте (по крайне мере, устно), не теряете ли вы решения! Какие это преобразования? Чаще всего, сокращение на что-то или деление на что-то. Так, например, при делении на нужно проверить, являются ли функции решениями дифференциального уравнения. В то же время при делении на необходимость в такой проверке уже отпадает – по причине того, что этот делитель не обращается в ноль.

Перечисленные тонкости также теряют актуальность, если в задаче требуется найти только частное решение (см., например, Пример №2 первого урока).

Следующий диффур – самостоятельно:

Решить дифференциальное уравнение

Полное решение и ответ в конце урока. Попробуйте для тренировки и здесь выразить общее решение.

В заключительной части урока рассмотрим еще пару характерных задач по теме:

Решить дифференциальное уравнение

Решение: «любимая функция» 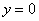не является решением, что убавляет хлопот. Идём проторенной дорогой. Данное уравнение является однородным, проведем замену:

После замены проводим максимальные упрощения:

Разделяем переменные:

Интегрируем:

Интеграл левой части можно найти двумя способами: методом выделения полного квадрата или методом неопределенных коэффициентов. Как я уже отмечал, в диффурах удобнее использовать второй метод (если, конечно, многочлен можно разложить на множители)

Здесь многочлен на множители раскладывается: можно решить квадратное уравнение , найти его корни и в результате: . Опытные студенты способны выполнить подбор корней и устно.

Методом неопределенных коэффициентов получим сумму дробей:

Таким образом:

Получившийся общий интеграл упрощаем:

И только после упрощений выполняем обратную замену:

Ответ: общий интеграл:

Решить дифференциальное уравнение

Это пример для самостоятельного решения. Отмечу, что время от времени однородное уравнение встречается в виде дроби, и типичный пациент выглядит примерно так:

Наверное, многие обратили внимание, что во всех приведенных примерах мы не находили частные решения уравнений (задача Коши). Это не случайно. В практических заданиях
с однородными уравнениями частное решение требуют находить крайне редко, если честно, я даже не припомню таких случаев. Ну а если уж встретилась задача Коши в однородном уравнении, то, после изучения предыдущего урока, она не должна представлять для вас трудностей. Технология – точно такая же, как и для уравнений с разделяющимися переменными. Если уточнить, то почти всегда будут получаться не частные решения, а частные интегралы.

Существуют и более сложные однородные уравнения. Сложность состоит не в замене переменной или упрощениях, а в достаточно трудных или редких интегралах, которые возникают в результате разделения переменных. У меня есть примеры решений таких однородных уравнений – страшненькие интегралы и страшненькие ответы. Но о них не будем, иначе к большинству читателей во сне явится Александр Емелин известный персонаж с формулами на полосатом свитере.

И, для полноты картины, рекомендую изучить статью Линейные неоднородные дифференциальные уравнения.

Решения и ответы:

Пример 2: Решение: Проверим уравнение на однородность:
Вместо подставляем , вместо подставляем :

Все лямбды сократились, и получилось исходное уравнение, значит, данное ДУ является однородным.
Очевидно, что 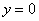является одним из решений данного уравнения.
Проведем замену: и максимально упростим уравнение:

Разделяем переменные, слева собираем «тэ», справа – «иксы»:

Интегрируем:

Надо сказать, с интегралом левой части повезло, бывает гораздо хуже.
Максимально упрощаем общий интеграл.
Если есть дроби, то от них лучше избавиться, умножаем каждую часть на 2:

Константу я переобозначу через :

(Если этот момент не понятен, читайте статью Дифференциальные уравнения первого порядка)
Собираем в правой части всё под логарифм, затем избавляемся от логарифмов

Обратная замена:

Умножаем все слагаемые на :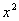

Ответ: общий интеграл:

Примечание: Решение 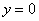входит в общее решение (когда ), поэтому его не нужно дополнительно указывать в ответе.

Проверка: Дифференцируем общий интеграл:

Получено исходное дифференциальное уравнение, значит, решение найдено верно.

Пример 4: Решение: Проверим уравнение на однородность:

Таким образом, данное уравнение является однородным.
Очевидно, что 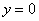является одним из решений уравнения.
Проведем замену:


После подстановки проводим максимальные упрощения:

Разделяем переменные и интегрируем:

Новорожденный общий интеграл получен, здесь константу я не стал загонять под логарифм, в данном случае – это ни к чему. Использовать или не использовать этот прием с константой – понимание придет с опытом.
Упрощать особо нечего, поэтому проводим обратную замену: :

Общий интеграл можно упростить:

Ответ: общий интеграл: . Ещё одно решение:
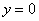
Примечание: здесь решение 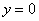не вошло в общий интеграл (т.к. не существует соответствующего значения константы), поэтому его следует указать дополнительно!

Пример 6: Решение: Преобразуем уравнение:

Очевидно, что 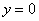является решением.
Данное уравнение является однородным, проведем замену:


Максимально упрощаем:

Разделяем переменные и интегрируем:

Упрощать нечего, поэтому проводим обратную замену :

Ответ: общий интеграл: . Ещё одно решение:

Примечание: также здесь можно выразить и общее решение: , для этого сразу после интегрирования константу следует загнать под логарифм.

Пример 8: Решение: Данное ДУ является однородным, проведем замену:





Обратная замена:

Ответ: общий интеграл:

Линейные дифференциальные уравнения первого порядка.
Примеры решений

На данном уроке мы рассмотрим алгоритм решения третьего типа дифференциальных уравнений, который встречается практически в любой контрольной работе – линейные неоднородные дифференциальные уравнения первого порядка. Для краткости их часто называют просто линейными уравнениями. Материал не представляет особых сложностей, главное, уметь уверенно интегрировать и дифференцировать.

Начнем с систематизации и повторения.

На что в первую очередь следует посмотреть, когда вам предложено для решения любое дифференциальное уравнение первого порядка? В первую очередь необходимо проверить, а нельзя ли у данного диффура разделить переменные? Если переменные разделить можно (что, кстати, далеко не всегда очевидно), то нужно использовать алгоритмы и приемы решения, которые мы рассмотрели на первом уроке – Дифференциальные уравнения первого порядка. Советую посетить этот урок чайникам и всем читателям, которые чувствуют, что их знания и навыки в теме пока не очень хороши.

Если переменные в ДУ разделить не удалось, переходим к следующему этапу – проверяем, а не является ли уравнение однородным? Проверку обычно выполняют мысленно или на черновике, с самим алгоритмом проверки и образцами решения однородных уравнений можно ознакомиться на втором уроке – Однородные дифференциальные уравнения первого порядка.

Если переменные разделить не удалось, и уравнение однородным не является, то в 90% случаев перед вами как раз линейное неоднородное уравнение первого порядка.

Линейное уравнение первого порядка в стандартной записи имеет вид:

Что мы видим?
1) В линейное уравнение входит первая производная .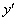
2) В линейное уравнение входит произведение , где – одинокая буковка «игрек» (функция), а – выражение, зависящее только от «икс».
3) И, наконец, в линейное уравнение входит выражение , тоже зависящее только от «икс». В частности, может быть константой.

Примечание: Разумеется, в практических примерах эти три слагаемых не обязаны располагаться именно в таком порядке, их спокойно можно переносить из части со сменой знака.

Перед тем, как перейти к практическим задачам, рассмотрим некоторые частные модификации линейного уравнения.

– Как уже отмечалось, выражение может быть некоторой константой (числом), в этом случае линейное уравнение принимает вид:

– Выражение тоже может быть некоторой константой , тогда линейное уравнение принимает вид: . В простейших случаях константа равна +1 или –1, соответственно, линейное уравнение записывается еще проще: или .

– Рядом с производной может находиться множитель , зависящий только от «икс»: – это тоже линейное уравнение.

Решить дифференциальное уравнение

Решение: Данное уравнение является линейным и имеет простейший вид: .

3. Существование и единственность решений дифференциального уравнения

1. Автономные уравнения на прямой

Неособая точка. Если точка $x_0$ является неособой, то есть $f(x_0)≠0$, решение находится по формуле Барроу, которую мы обсуждали в предыдущей главе:

Если вы не доверяете теореме об обратной функции, можно рассуждать так. Известно, что $f(x_0)≠0$; допустим для определённости (как говорят «без ограничения общности»), что $f(x_0)>0$ (обратный случай рассматривается полностью аналогично). Поскольку функция $f$ непрерывна вблизи точки $x_0$, существует её окрестность $U$, на которой функция $f$ принимает только положительные значения. Таким же свойством обладает и функция $\frac<1>$, являющаяся подынтегральным выражением в (3) . Следовательно, функция $F$ монотонно возрастает на $U$. Следовательно, у неё существует обратная функция.

Рассмотрим теперь второй возможный случай.

Особая точка. Если $f(x_0)=0$, очевидно, решением является константа $x=x_0$: в точке $x_0$ уравнение требует, чтобы производная решения была нулевой, то есть решение в этой точке не растёт и не убывает, а значит остаётся постоянным. ∎

Вот такое доказательство. Убедительно?

Тут нужно сделать театральную паузу. А потом рассмотреть пример.

Как так может быть? Мы доказали неверную теорему? Математика — сплошной обман?

А вот и нет. У нас просто ошибка в доказательстве: разбирая второй случай, мы сказали, что существует решение $x=x_0$, но мы не доказали на самом деле, что других решений с таким начальным условием нет. Рассуждение о том, что решение с нулевой производной в некоторой точке «в этой точке не растёт и не убывает, а значит остаётся постоянным» легко опровергается: функция $x=t^3$ имеет нулевую производную в нуле, но при этом не является константой вблизи нуля.

Значит ли это, что теорема неверна? Снова нет. Теорема верна. Если вы внимательно посмотрите на её формулировку, то увидите, что уравнение, рассмотренное в примере, не удовлетворяет условию теоремы: правая часть $f(x)=x^<2/3>$ не является гладкой функцией в точке $x=0$: её производная там стремится к бесконечности.

Этот пример показывает, что требование $C^1$-гладкости правой части в формулировке теоремы 1 является важным: если его выбросить, теорема оказывается неверной. (Впрочем, его можно ослабить: вместо гладкости требовать липшицевости правой части.) Если же это требование выполняется, теорема верна. Докажем это.

Пусть $f(x_0)=0$. Функция $x(t)=x_0$ в этом случае всегда будет решением уравнения $\dot x=f(x)$. Нам необходимо показать, что других решений не будет, то есть исключить ситуацию, когда решение принимает значение $x_0$ (быть может, на некотором отрезке по оси $y$), а затем «убегает» из этой точки. Мы докажем, что если $f\in C^1$, то «побег» запрещен.

Доказываем от противного: пусть удалось убежать из точки $x_0$ в какую-то точку $x_2$, то есть существует решение $x=x(t)$, принимающее значение $x_0$ при $t=t_0$ и значение $x_2$ при каком-то другом $t=t_2$. Возьмём какую-то точку $x_1$ между $x_0$ и $x_2$. Поскольку решение непрерывно, должен существовать момент времени $t_1\in (t_0, t_2)$, в который мы окажемся в точке $x_1$ (то есть $x(t_1)=x_1$). Посчитаем время $t_2-t_1$, которое потребуется, чтобы от $x_1$ добраться до $x_2$, см. рис. 1 .

Если мы это докажем, то придём к противоречию с предположением, что нам удалось убежать за конечное время из $x_0$ в какую-то другую точку: понятно, что $t_2 — t_0 > t_2 — t_1$ и если вторая величина может быть сколь угодно большой, то первая не может быть конечным числом.

Смысл. Переводя на русский язык, можно сказать, что гладкая функция вблизи своего нуля растёт не быстрее, чем некоторая линейная функция. В это легко поверить. Предположим для простоты, что $x_0=0$. Возьмём функцию $f(x)$, такую, что $f(0)=0$. Вблизи нуля она хорошо приближается касательной $y=f'(0)x$, хотя и может проходить чуть выше или чуть ниже касательной. Если построить прямую, наклон которой будет несколько больше, чем наклон касательной, то график функции окажется запертым между этой прямой и её отражением относительно горизонтальной оси. (См. рис 2 .)

2. Общий случай

Существует такая окрестность $U\ni t_0$, что на $U$ существует и единственно решение $x\colon U\to \mathbb R^n$ задачи (6) .

3. Метод разделения переменных: магия продолжается

Обоснование. Чтобы магия не казалось такой загадочной, приведём обоснование этого метода. Это не самое лучшее с моей точки зрения обоснование: в нём слишком много формул и слишком мало картинок. Чуть позже мы обсудим более геометрическое доказательство, но оно потребует дополительных построений.

Итак, пусть $x=x(t)$ — функция, удовлетворяющая соотношению (8) . Продифференцируем почленно это соотношение по переменной $t$.

Особые решения дифференциальных уравнений

Решение дифференциального уравнения

называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение

Выпишем условие касания двух кривых и в точке с абсциссой :

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .

Полагая , находим, что условия (7) принимают вид

Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).

г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).

Огибающей семейства кривых

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.

Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.

Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

где и — постоянные;

Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.

Пример 2. Найти особые решения дифференциального уравнения

а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда

Это и есть C-дискриминантная кривая: она состоит из двух прямых и .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке

где — область допустимых значений .

Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места точек заострения (возврата);

3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;

3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.

Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).

Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

Решение. Особое решение, если оно существует, определяется системой

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).

Пример 4. Найти особые решения дифференциального уравнения

Решение. Дифференцируем (23) по

Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

Решение. Найдем . Исключая из системы уравнений получаем

Преобразовав уравнение (25) к виду , находим его общий интеграл .

Найдем . Исключая из системы уравнений будем иметь

Итак, из (26) и (27) имеем

Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.

Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .

Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).

Пример 6. Найти особые решения дифференциального уравнения

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда

Подставляя (29) в (28), найдем уравнение :

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

Дифференцируя обе части (28) по и учитывая, что , будем иметь

Приравнивая нулю первый множитель , получаем (29), а соотношение дает

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

Подставляя (34) в (33), получаем уравнение .

Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).