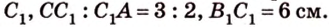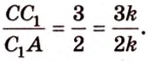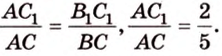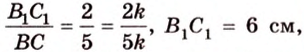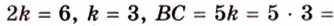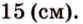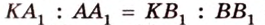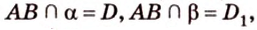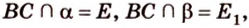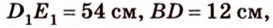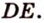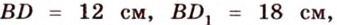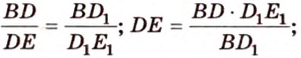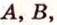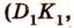Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
На каждой прямой и в каждой плоскости могут быть отмечены точки.
Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d .
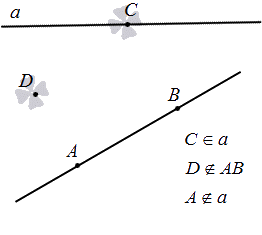
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Чтобы обозначить, принадлежит точка плоскости или точка прямой, используют знак « ∈ ». Если в условии дано, что точка A лежит на прямой a , тогда это имеет такую форму записи A ∈ a . В случае, когда точка А не принадлежит, тогда другая запись A ∉ a .
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В , то прямую, проходящую через них можно назвать данными буквами, например, прямая А В . Рассмотрим рисунок, приведенный ниже.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Если дано, что точки А и Р – концы отрезка, значит, его обозначение примет вид Р А или А Р . Так как обозначения отрезка и прямой совпадают, рекомендовано дописывать или договаривать слова «отрезок», «прямая».
Краткая запись принадлежности включает в себя использование знаков ∈ и ∉ . Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂ . Если в условии дано, что отрезок А Р принадлежит прямой b , значит, и запись будет выглядеть следующим образом: А Р ⊂ b .
Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А , В , С , которые принадлежат одной прямой, а точка В лежит между А и С , следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
Любая точка O , находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O , а другие – по другую сторону луча.
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
Две прямые на плоскости могут пересекаться.
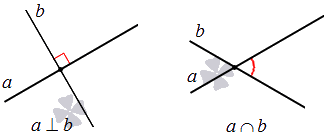
Данный случай показывает, что имеется одна общая точка, которую называют пересечением прямых. Вводится обозначение пересечение знаком ∩ . Если имеется форма записи a ∩ b = M , то отсюда следует, что заданные прямые a и b пересекаются в точке M .
При пересечении прямых имеем дело образовавшимся углом. Отдельному рассмотрению подвергается раздел пересечения прямых на плоскости с образованием угла в 90 градусов, то есть прямого угла. Тогда прямые называют перпендикулярными. Форма записи двух перпендикулярных прямых такая: a ⊥ b , а это значит, что прямая a перпендикулярна прямой b .
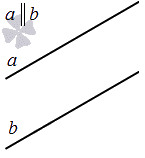
Две прямые на плоскости могут быть параллельны.
Только в том случае, если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны. Используется обозначение, которое можно записать при заданной параллельности прямых a и b : a ∥ b .
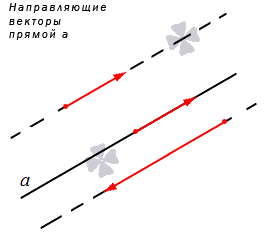
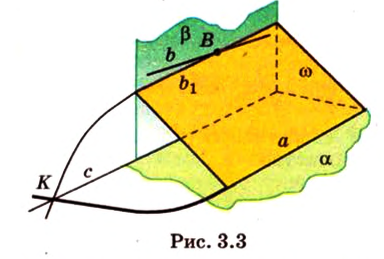
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
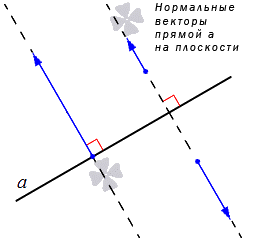
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
- если две прямые параллельны третьей, тогда они все параллельны;
- если две прямые перпендикулярны третьей, тогда эти две прямые параллельны;
- если на плоскости прямая пересекла одну параллельную прямую, тогда пересечет и другую.
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
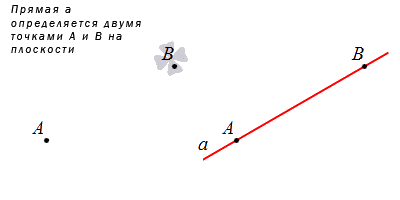
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
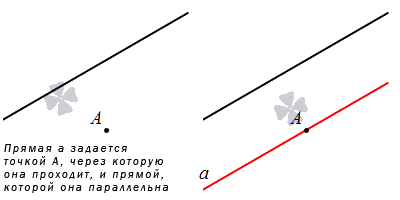
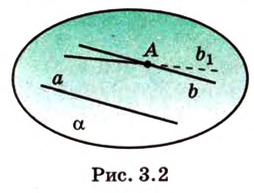
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
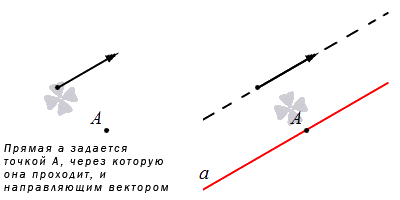
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
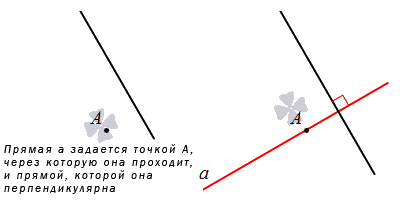
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
Взаимное расположение прямых в пространстве, прямой и плоскости с примерами решения
Содержание:
Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.
Взаимное расположение прямых в пространстве
Если рассматривать две прямые на плоскости, то они либо не пересекаются, либо пересекаются только в одной точке. Те прямые, которые не пересекаются и лежат в одной плоскости, называют параллельными. А те, которые пересекаются, имеют особое название только в одном случае — если пересекаются под прямым углом. Такие прямые называются перпендикулярными.
Существуют ли в пространстве прямые, которые пересекаются и которые не пересекаются? Ответ на этот вопрос дают образы окружающего мира. Имеют ли такие прямые свое название и как их различать — вы узнаете из этого параграфа.
По аксиоме стереометрии, если две прямые пересекаются, то через них можно провести единственную плоскость. Это означает, что любые две пересекающиеся прямые определяют плоскость, а плоскости, в свою очередь, — пространство.
Итак, в пространстве прямые, расположенные в одной плоскости, могут пересекаться или быть параллельными. По аксиоме параллельных прямых, через точку вне прямой можно провести единственную прямую, параллельную данной. По следствию из аксиомы стереометрии, через прямую и точку вне ее можно провести единственную плоскость. Поэтому выходит, что две параллельные прямые задают плоскость.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если две произвольные прямые
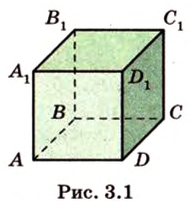
Рассмотрим модель куба, изготовленного из «проволочных отрезков», лежащих на соответствующих прямых (рис. 3.1). Среди прямых, на которых лежат ребра куба, есть такие, которые не пересекаются и лежат в одной плоскости ( 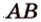
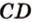
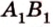
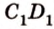
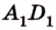
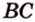
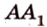
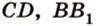
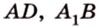
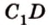
Две прямые пространства, которые не пересекаются и не параллельны, называются скрещивающимися.
Понятно, что две скрещивающиеся прямые не могут лежать в одной плоскости. Поэтому говорят, что две прямые скрещиваются, если их нельзя поместить в одну плоскость. Для определения скрещивающихся прямых используют символ 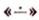

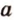
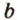
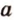
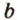
Итак, расположение двух прямых в пространстве может быть следующим:
- прямые пересекаются, если они имеют только одну общую точку;
- прямые параллельны, если они не пересекаются и лежат в одной плоскости;
- прямые скрещиваются, если они не пересекаются и не параллельны;
- прямые совпадают, если они имеют хотя бы две общие точки.
Рассмотрим свойства, которыми обладают параллельные прямые в пространстве.
Теорема 1
Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Пусть 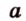
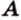
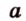
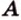
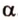
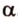

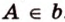
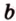
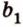
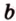
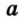

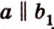
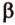
Итак, 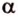
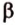
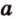
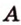
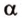
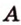
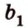
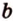
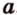
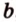
Теорема 2 (признак параллельности прямых)
Если две прямые параллельны третьей прямой, то они параллельны между собой.
Пусть прямые 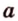
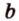
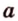
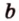
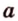
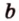
По условию 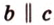
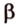
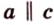
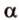
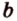
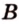
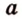
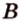
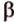
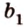

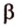
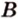
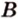
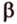
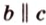
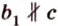
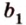
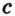
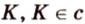

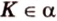
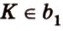
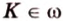
Т.е. точка 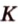
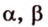
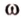
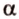
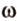
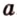
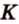
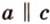
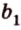
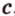
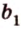
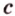
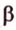
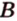
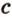
Поэтому прямые 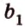
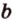
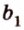
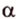
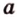
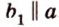
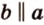
Свойство скрещивающихся прямых выражает признак: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (предлагаем доказать это самостоятельно).
Взаимное расположение прямой и плоскости в пространстве
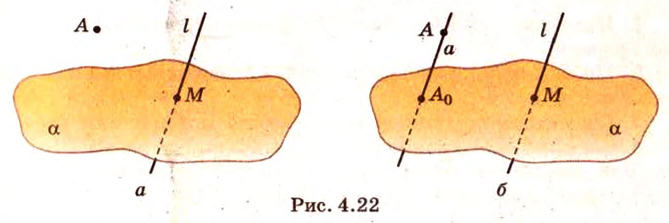
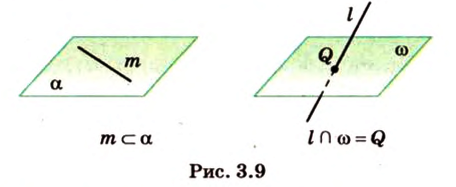
Прямая является подмножеством точек плоскости. Она состоит из множества точек. Такие рассуждения приводят к тому, что прямая и плоскость могут иметь множество общих точек, одну или ни одной общей точки. Случаи, когда прямая принадлежит плоскости и когда прямая пересекает плоскость, нам известны (рис. 3.9). Другие случаи расположения прямой и плоскости рассмотрим в следующих параграфах.
Теорема 3
Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая также пересекает эту плоскость.
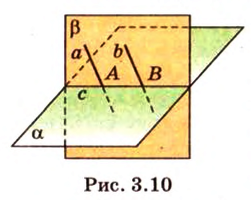
Пусть даны параллельные прямые 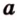
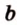
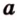
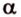
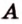
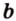
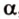
Обозначим 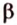
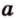
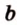
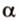
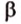
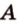

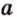
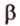
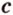
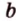
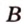
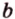
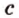
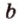
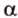
Допустим, что прямая 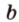
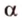
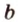
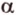
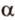
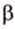
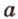
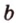
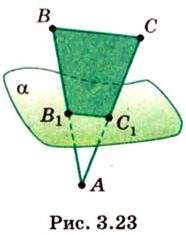
Пример №1
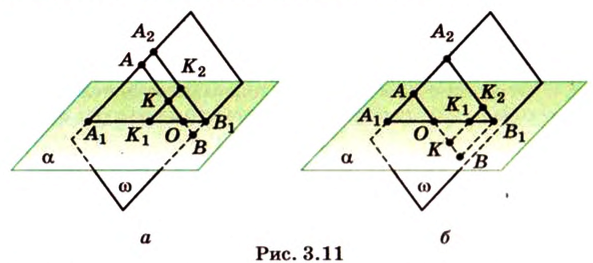
Отрезок 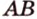
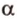
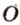
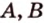
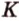
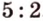
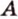
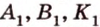
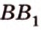
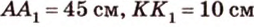
Поскольку прямые 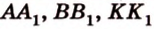
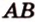

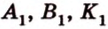
Проведем в плоскости 
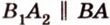
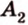
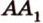
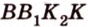
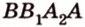
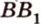
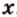
Тогда 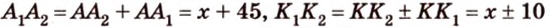
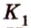
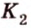
Из подобия треугольников 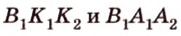
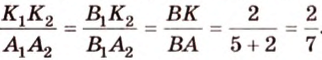
Итак, 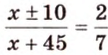
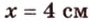
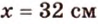
Ответ. 4 см или 32 см.
Отметим, что прямая пересекает плоскость, когда у нее с плоскостью одна общая точка.
Параллельность прямой и плоскости
Рассмотренные в параграфах 3.1 и 3.2 случаи не исчерпывают всех возможных вариантов расположения прямой относительно плоскости. Рассмотрим случай, когда у прямой с плоскостью нет ни одной общей точки. В таком случае говорят, что прямая параллельна плоскости.
Прямая называется параллельной плоскости, если не имеет с ней ни одной общей точки.
Параллельность прямой и плоскости обозначают символом 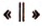
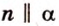
Теорема 4 (признак параллельности прямой и плоскости)
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
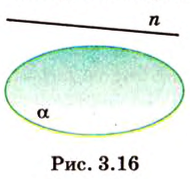
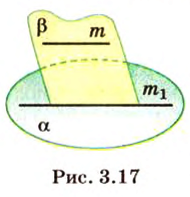
Пусть 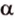
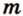
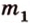
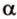
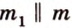
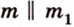
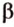
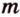
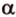
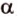
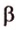
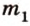
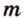
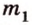
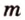
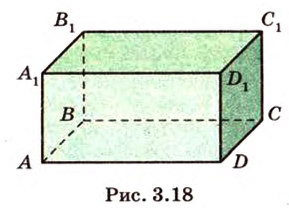
Отрезок называется параллельным плоскости, если он принадлежит прямой, которая параллельна плоскости. Например, и помещении, имеющем форму прямоугольного параллелепипеда, стыки стен с потолком параллельны полу, и наоборот -стыки стен с полом параллельны потолку и т.д. Аналогично можно рассматривать такое расположение на модели прямоугольного параллелепипеда (рис. 3.18):
Следствие 1. Если прямая параллельна плоскости, то через каждую точку этой плоскости на ней можно провести пря мую, параллельную данной прямой.
Например, на плоскости 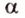
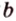
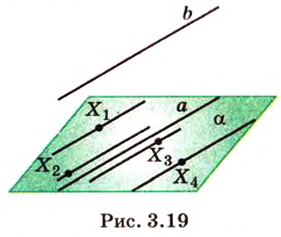
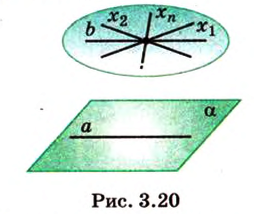
Следствие 2. Существует множество прямых, параллель пых одной и той же плоскости.
Например, вне плоскости 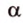
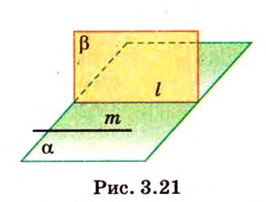
Следствие 3. Если прямая параллельна каждой из пересекаю щихся плоскостей, то она параллельна и прямой их пересечения.
Например, на рисунке 3.21 изображены 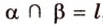
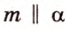
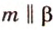
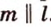
Итак, через точку 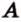
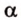
- — множество прямых, параллельных плоскости
,
- — одну прямую
, параллельную прямой
плоскости
,
- — множество прямых, скрещивающихся с прямой
плоскости
Пример №2
Докажите, что все прямые, пересекающие одну из двух скрещивающихся прямых и параллельные другой, лежат в одной плоскости.
Дано: прямые 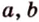
Доказать, что все прямые, пересекающие 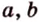
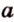
Проведем несколько произвольных прямых 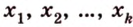
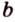
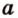
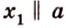
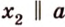
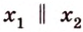
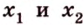
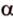
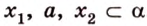
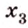
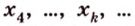
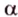
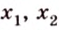
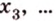
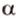
Почему именно так?
Скрещивающиеся прямые 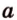
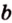

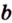
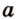
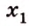
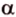
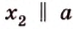

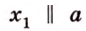
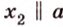
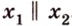

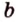
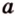
Пример №3
Плоскость 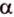
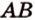
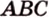
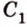
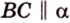
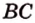
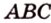
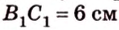
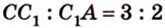
Дано: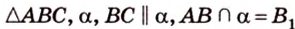
Найти: 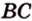
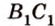
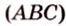
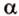
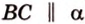
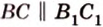
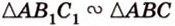
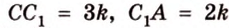
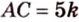
Почему именно так?
Плоскость треугольника 
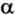
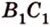
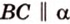
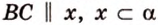
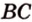
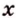
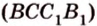
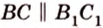
Взаимное расположение двух плоскостей в пространстве. Параллельные плоскости
Если рассматривать две плоскости в пространстве, то их расположение зависит от наличия общих точек.
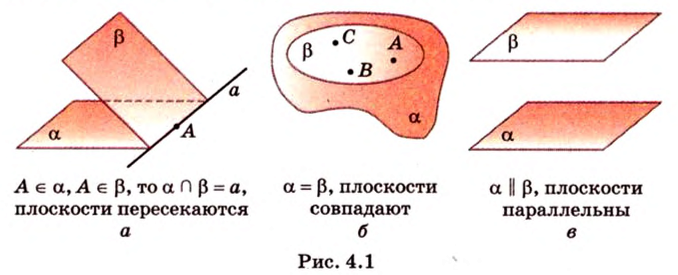
1. Если у двух плоскостей имеется одна общая точка, то они пересекаются по прямой, которая проходит через эту точку (аксиома расположения) (рис. 4.1, а). При наличии двух общих точек ситуация не изменится: через произвольные две точки можно провести только одну прямую, которая будет общей для этих двух плоскостей, т.е. они пересекаются по этой прямой.
Итак, если две плоскости имеют одну или много общих точек, лежащих на одной прямой, то эти плоскости пересекаются.
2. Как известно, через три произвольные точки пространства, не лежащие на одной прямой, можно провести плоскость, и притом только одну (следствие из аксиом стереометрии). Тогда очевидно, что если две плоскости будут иметь три и больше общих точек, не лежащих на одной прямой, то они будут накладываться (рис. 4.1, б). В таком случае говорят, что плоскости совпадают.
Отсюда вытекает, что плоскости совпадают, если они имеют:
- а) общую прямую и точку, не принадлежащую ей;
- б) две общие прямые, которые пересекаются;
- в) хотя бы три общие точки, не лежащие на одной прямой.
3. Если две различные плоскости не имеют ни одной общей точки, то они называются параллельными (рис. 4.1, в). Для обозначения параллельности плоскостей используют символ 
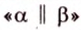
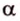
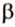
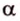
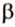
Итак, плоскости в пространстве могут: пересекаться, совпадать или быть параллельными.
Модели параллельных плоскостей встречаются довольно часто: полки в шкафу, двойные стекла в оконной раме, пол и потолок, перекрытия в многоэтажном доме, ровно сложенные в упаковках диски, учебники и т.д. Выяснить, параллельны ли плоскости, позволяет признак параллельности плоскостей.
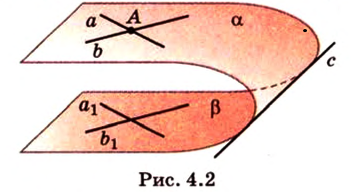
Теорема 1
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Пусть 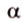
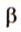
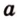
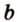
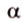
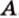
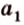
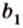
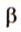
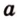
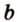
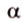
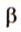
Допустим, что 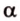
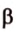

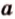
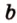
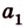
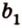
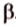
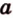
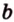
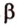
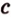
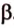
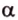
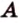
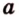
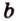

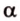
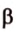
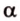
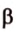
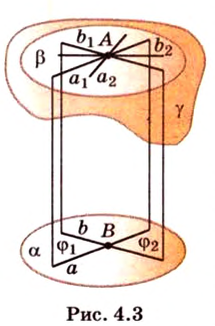
Теорема 2
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Пусть 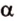
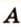
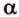
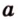
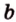
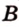
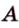
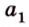
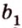
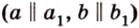
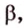
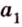
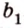
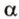
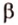
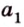
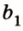
Допустим, что существует другая плоскость 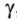
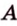
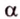
1. Построим плоскость 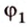
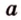
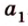
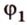
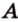
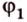
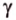
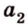
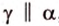
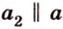
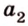
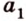
2. Построим плоскость 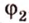
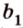
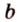
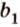
Итак, имеем, что через две пересекающиеся прямые 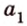
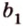
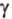
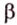
Пример №4
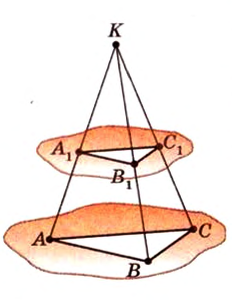
Точка 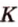
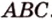
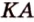
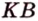
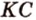
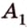
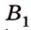
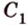

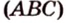
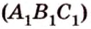
Дано: 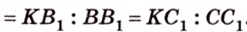
Доказать: 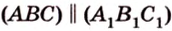
По условию задачи: 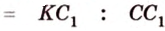
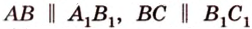
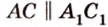
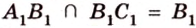
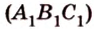
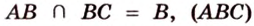
Итак, по признаку параллельности плоскостей, имеем, что 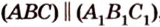
Почему именно так?
По обобщенной теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Поэтому, учитывая условие задачи, получаем параллельность трех пар соответствующих прямых: 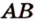
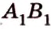
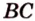
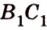
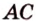
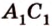
Точками 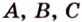
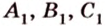
Пример №5
Даны две параллельные плоскости 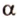
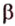
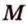
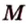
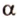
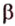
Пусть плоскости 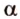
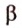
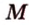
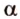
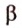
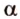
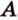
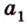
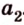
Через точку 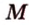
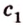
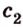
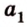
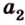
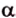
Две пересекающиеся прямые определяют единственную плоскость, пусть это будет плоскость 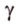
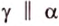
Аналогично доказывается, что 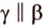
Через точку 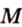
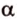
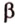
Ответ. Плоскость.
Почему именно так?
Точка 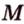
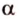
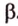
Свойства параллельных плоскостей
Параллельные плоскости имеют определенные свойства. Рассмотрим их.
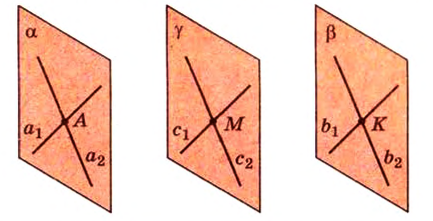
Свойство 1. Если две параллельные плоскости пересечь третьей, то прямые их пересечения параллельны.
Пусть 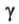
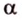
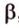
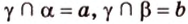
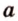
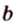
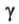
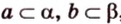
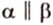
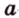
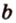
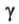
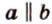
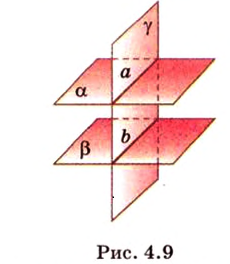
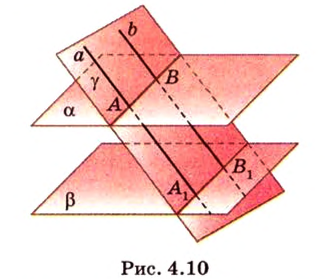
Свойство 2. Параллельные плоскости, пересекая две параллельные прямые, отсекают на них равные отрезки.
Пусть 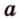
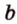
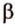
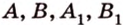
Поскольку прямые 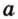
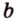
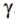
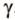
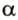
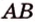
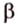
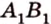
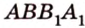
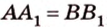
Свойство 2 иногда формулируется так: отрезки параллельных прямых, находящиеся между двумя параллельными плоскостями, равны.
Свойство 3. Две плоскости, параллельные третьей плоскости, параллельны между собой.
Пусть 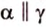
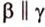
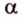
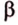
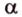
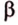
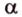
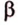
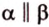
Пример №6
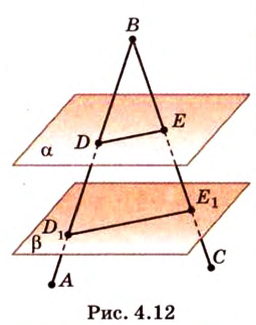
Докажите, что плоскость, пересекающая одну из двух параллельных плоскостей, пересекает и другую плоскость.
Дано: 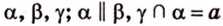
Доказать: плоскость у пересекается с плоскостью 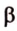
Докажем, что плоскость 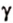
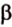
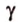
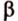
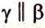
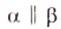
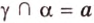

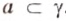
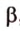
Почему именно так?
Для доказательства требования задачи важно выбрать метод доказательства: прямой или от противного. В общих случаях чаще используют метод от противного. Сделав предположение, противоположное требованию задачи, мы приходим к выводу: 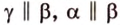
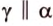
Итак, плоскость, пересекающая одну из двух параллель ных плоскостей, пересекает и другую.
Пример №7
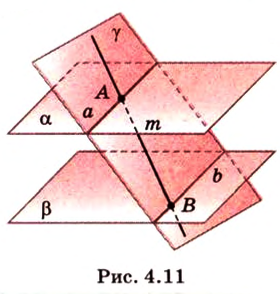
Докажите, что прямая, которая пересекает одну из параллельных плоскостей, пересекает и другую.
Дано: 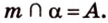
Доказать: прямая 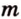
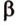
Построим произвольную плоскость 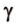
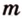
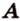
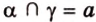
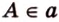
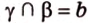
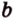
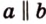
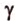
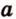
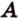
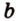
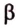
Можно было бы доказать требование задачи методом от противного: предположив, что прямая 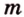
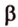
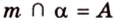
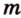

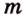
Итак, любая прямая, пересекающая одну из двух параллельных плоскостей, пересекает и другую.
Пример №8
Две параллельные плоскости 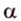
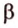
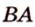
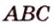
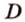
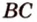
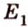
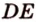
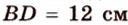
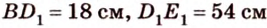
Дано: плоскости 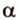
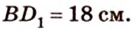
Найти:
Пусть 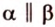
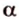
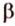
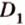
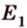
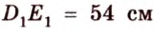
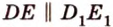
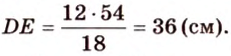
Ответ. 36 см.
Почему именно так?
Через точки 
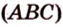
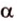
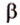
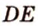
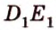
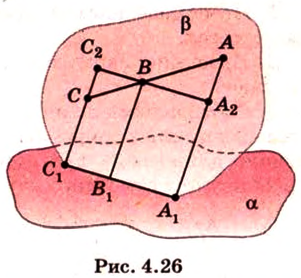
Параллельное проецирование. Изображение плоских и пространственных фигур на плоскости
Чтобы изобразить пространственные фигуры на плоскости, прибегают к разным методам. Один из них — параллельное проецирование.
Параллельное проецирование — это метод изображения произвольной геометрической фигуры на плоскости, при котором все точки фигуры переносятся на плоскость по прямым, параллельным заданной, называющейся направлением проецирования.
Модели параллельного проецирования можно сравнить с тенью на плоской поверхности стены или земли при солнечном освещении. Итак, чтобы выполнить параллельное проецирование, сначала задают фигуру и плоскость, на которую проецируют, — плоскость проекции. Далее задают прямой направление проецирования — проецирующую прямую. Она должна пересекать плоскость проекции.
Пусть заданы произвольная плоскость 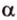
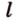
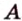
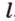
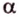
Проведем через точку 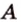
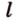
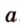
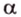
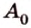
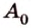
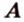
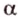
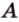
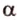
Каждая геометрическая фигура состоит из точек. Поэтому, проецируя последовательно точки фигуры на плоскость, получаем изображение, которое называют проекцией этой фигуры, и способ выполнения изображения — параллельным проецированием.
Отметим, что если точка принадлежит проецирующей прямой, ее проекцией будет точка пересечения прямой с плоскостью (точка 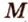
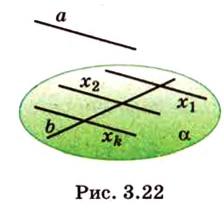
Рассмотрим параллельное проецирование для изображения геометрических фигур на плоскость. Пусть 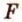
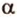
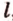
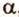
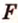
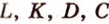
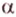
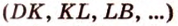
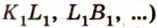
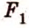
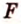
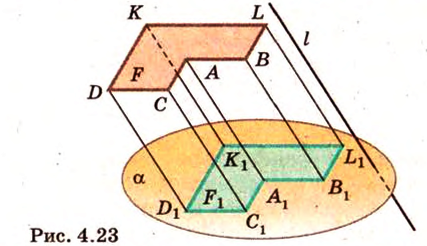
Для параллельного проецирования важно знать его направление. От него зависит общий вид изображения проекции. Например, проекцией отрезка, параллельного проецирующей прямой, будет точка (рис. 4.24, а), а проекцией отрезка, не параллельного проецирующей прямой, — отрезок (рис. 4.24, б).
Итак, параллельное проецирование имеет свои свойства для прямых и отрезков, не параллельных направлению проецирования:
- Проекцией прямой является прямая, а проекцией отрезка — отрезок.
- Проекции параллельных прямых параллельны или совпадают.
- Соотношения длин отрезков одной прямой или параллельных прямых сохраняются (рис. 4.24, б), т.е. равны соотношению длин своих проекций, в частности середина отрезка проецируется в середину его проекции.
Отметим, что длины проекций отрезков, параллельных плоскости проекций, сохраняются, т.е. равны длинам самих отрезков. Отсюда вытекает, что плоская фигура, плоскость которой параллельна плоскости проекции, проецируется в равную себе фигуру.
Приведем некоторые свойства изображения фигуры на плоскости, вытекающие из вышеописанного построения.
Прямолинейные отрезки фигуры изображаются на плоскости рисунка отрезками (рис. 4.24, б).
Действительно, все прямые, которые проецируют точки отрезка 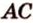
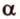
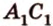
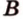
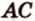
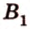
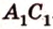
Отметим, что рассмотренные выше отрезки, которые проецируются, не параллельны направлению проецирования.
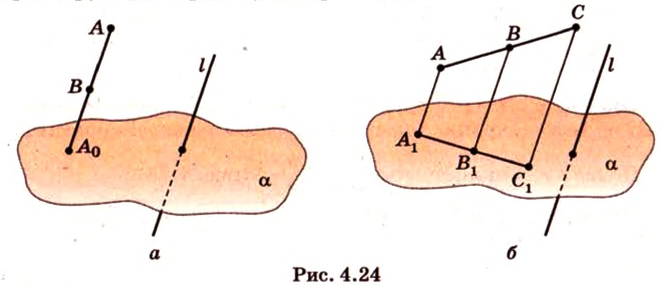
Параллельные отрезки фигуры изображаются на плоскости рисунка параллельными отрезками (рис. 4.25).
Пусть 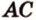
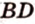
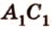
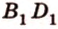
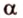
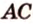
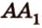
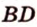
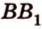
Соотношения длин отрезков одной прямой или параллельных прямых сохраняются при параллельном проецировании.
Покажем, например, что 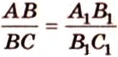
Прямые 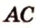
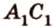
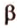
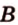

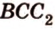
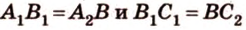
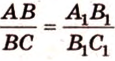
Пример №9
Дана параллельная проекция треугольника. Как построить проекции медиан этого треугольника?
При параллельном проецировании сохраняются соотношения отрезков прямой. Поэтому середина стороны треугольника проецируется в середину проекции этой стороны. Отсюда вытекает, что проекции медиан треугольника будут медианами его проекции.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Параллелограмм
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
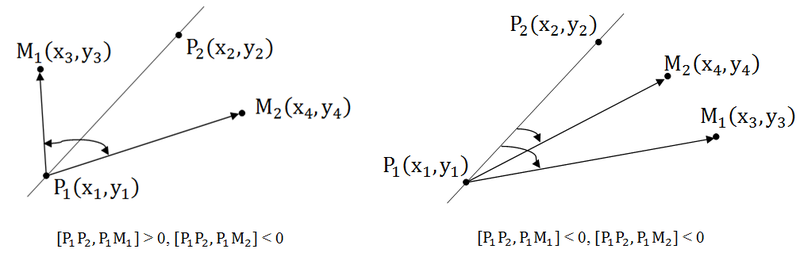
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
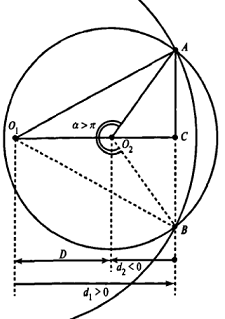
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
http://www.evkova.org/vzaimnoe-raspolozhenie-pryamyih-v-prostranstve-pryamoj-i-ploskosti
http://habr.com/ru/post/148325/
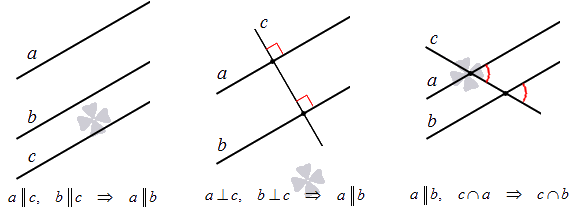
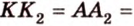
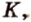
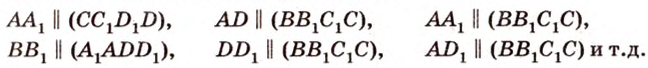
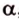 ,
,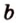 , параллельную прямой
, параллельную прямой 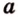 плоскости
плоскости  ,
, плоскости
плоскости