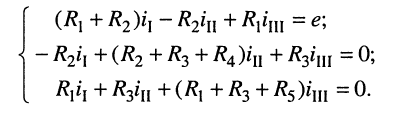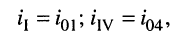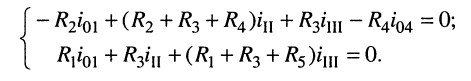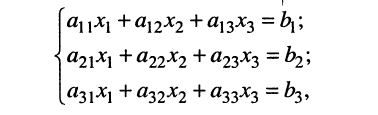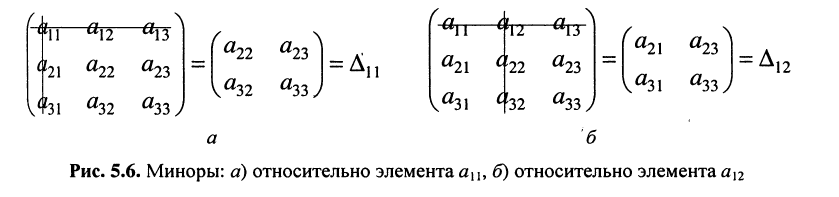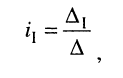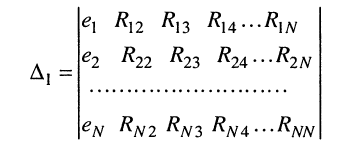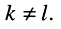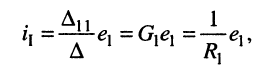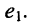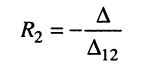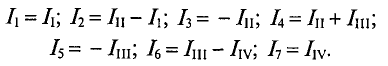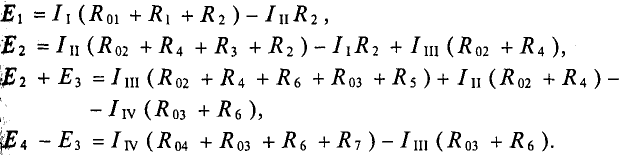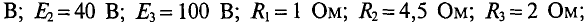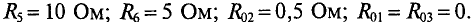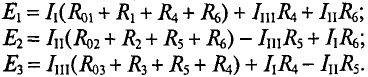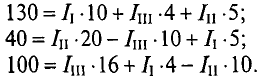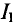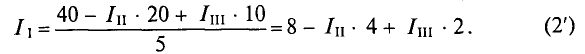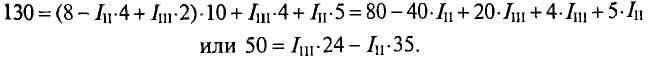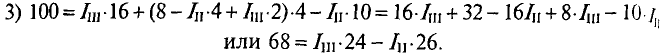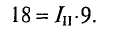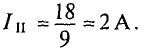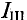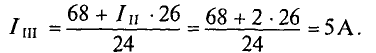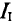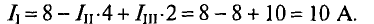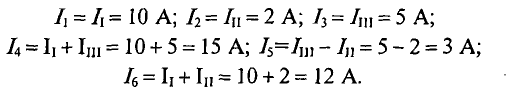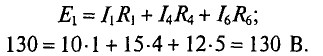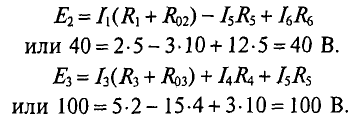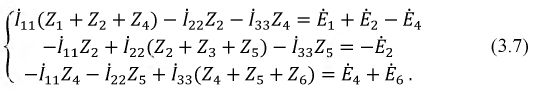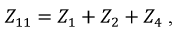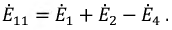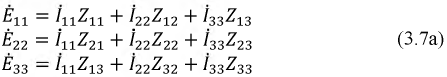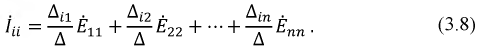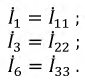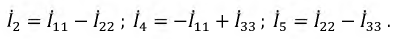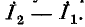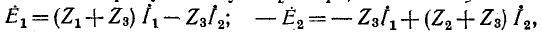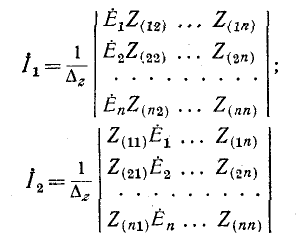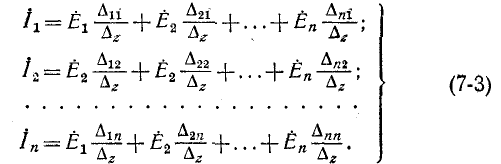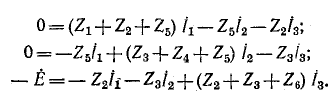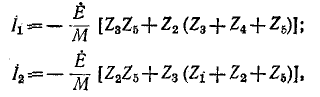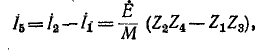Метод контурных токов
Содержание:
Метод контурных токов:
Контурным током называют условный ток, протекающий внутри независимого контура.
Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу
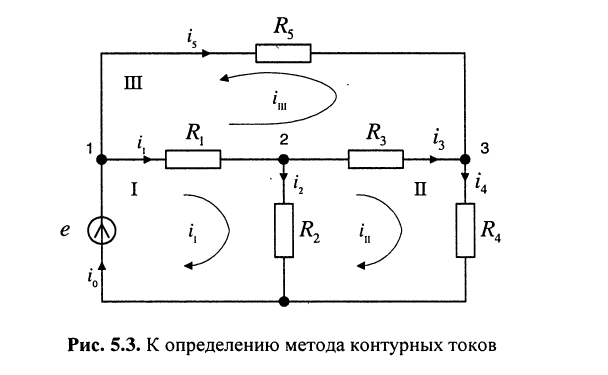
Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем:
Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.
Составление контурных уравнений
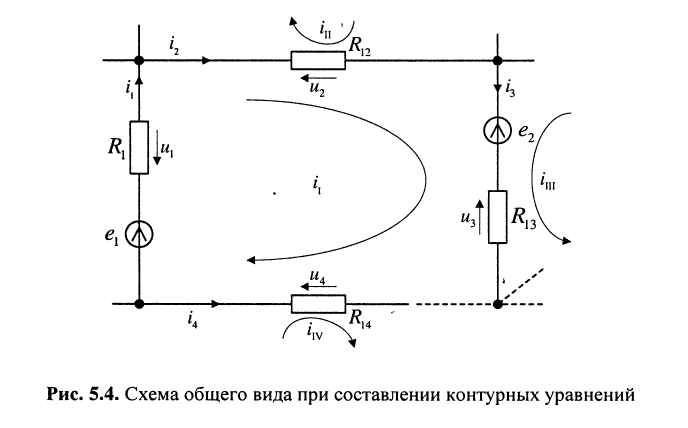
При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):
- цепь согласно (5.4) содержит
независимых контуров;
- в цепи имеются источники напряжения с ЭДС
- все
независимых контуров непосредственно связаны друг с другом, т. е. для к-го и 1-го контуров имеется хотя бы один элемент
который входит в оба эти контура, причём
При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:
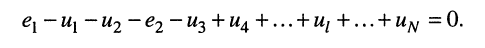
Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома:
или в общем виде:
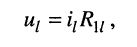
— ток в
-ой ветви;
— напряжение в
-ой ветви;
— сопротивление элемента, общего для 1-го и
-го контуров.
Подставим (5.6) в (5.5)
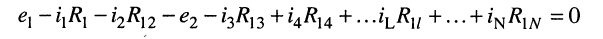
и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что:
Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):
Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид
Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:
- в левую часть каждого из уравнений входит N слагаемых, пропорциональных искомым контурным токам
- коэффициент при контурном токе
-го контура, для которого составляется уравнение, представляет собой арифметическую сумму сопротивлений этого контура;
- остальные слагаемые представляют собой произведение сопротивления элемента
общего для
-го и
-го контуров, на контурный ток 1-го контура; эти слагаемые входят в уравнение со знаком «+», если направления токов
-го и
-го контуров в элементе
совпадают; в противном случае они входят в уравнение с отрицательным знаком.
Аналогично записываются узловые уравнения для всех других контуров цепи, в результате чего образуется система контурных уравнений вида:
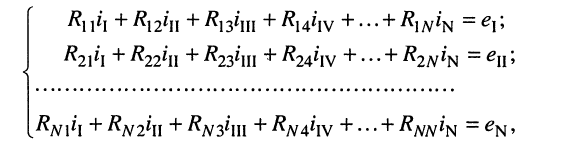
— собственное сопротивление k-го контура, оно определяется как арифметическая сумма сопротивлений всех элементов
-го контура;
— взаимное сопротивление
-го и
-го контуров цепи
, оно является сопротивлением элемента, общего для
-го и
-го контуров; слагаемые вида
входят со знаком «+» при совпадении направлений токов в этих контурах; если связь между
-ым и
-ым контурами осуществляется через несколько элементов активного сопротивления, то
представляет собой арифметическую сумму соответствующих взаимных сопротивлений, причём
— контурный ток
-го контура цепи;
— контурная ЭДС
-го контура цепи, представляющая собой алгебраическую сумму ЭДС независимых источников, имеющихся в контуре; слагаемые этой суммы имеют знак «+», если заданное направление отсчёта ЭДС источника совпадает с выбранным направлением отсчёта контурного тока.
Система контурных уравнений (5.9) составлена относительно неизвестных контурных токов и записана в канонической форме, а именно:
- контурные ЭДС, как свободные члены, записываются в правых частях уравнений;
- неизвестные контурные токи записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами контуров.
Пример 5.2.
Записать систему контурных уравнений для удлинителя (рис. 5.3).
Решение. Предварительно найдём собственные и взаимные сопротивления трёх контуров:
• собственное сопротивление 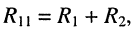
• взаимные сопротивления: со вторым контуром 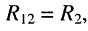
• собственное сопротивление 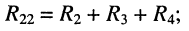
• взаимные сопротивления: с первым контуром 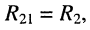
• собственное сопротивление 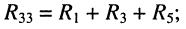
• взаимные сопротивления: с первым контуром 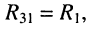
- направление контурного тока
совпадает с направлением контурного тока
и противоположно направлению контурного
- тока
- направления контурных токов
совпадают;
- в контуре I имеется контурный независимый источник с ЭДС, равной
а два других контура источников не имеют.
Теперь можно записать систему контурных уравнений, руководствуясь указанными ранее правилами:
Особенности составления контурных уравнений
Рассмотренные ранее цепи не содержали независимых источников тока, поэтому количество контурных уравнений согласно (5.4) равно количеству независимых контуров. Однако цепь может иметь несколько источников токов. В этом случае следует выбрать такое дерево цепи, при котором источники токов входили бы в число соединительных элементов. Тогда через каждый источник тока будет проходить ток только одного контура, который равен задающему току источника. Поэтому уменьшается как число неизвестных контурных токов, так и число контурных уравнений. Следовательно, если цепь содержит 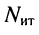
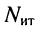
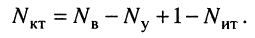
Пример 5.3.
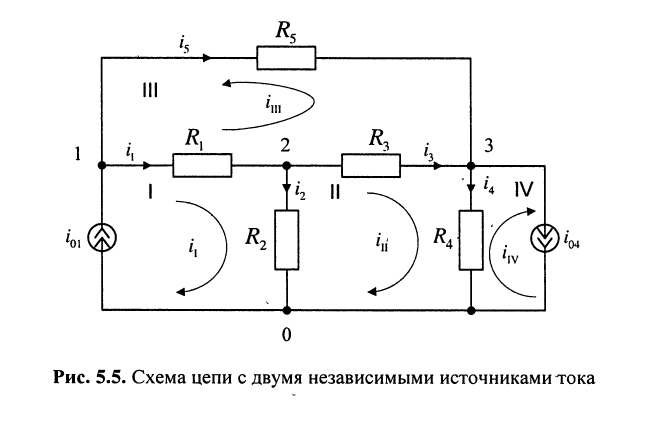
Записать систему контурных уравнений для цепи, схема которой изображена на рис. 5.5.
Решение. Цепь содержит два источника тока: в первом и четвёртом контурах, где контурные токи совпадают с токами источников:
поэтому достаточно записать только два контурных уравнения — для второго и третьего контуров.
В уравнении для третьего контура отсутствует слагаемое, содержащее ток 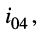
Важно:
метод контурных токов применяют в тех случаях, когда число контурных уравнений меньше числа узловых уравнений, а также при анализе колебаний в линейных электрических цепях произвольной конфигурации, содержащих все виды элементов.
Решение системы контурных (узловых) уравнений
Решение системы контурных (узловых) уравнений состоит в нахождении неизвестных контурных токов (узловых напряжений) для последующего вычислением токов и напряжений на элементах цепи. Если параметры цепи (сопротивления, проводимости, токи источников токов, ЭДС источников напряжений) заданы численно, то решение систем осуществляется с помощью специальных пакетов программ математического моделирования, например, Matlab или Matcad.
Основные понятия теории определителей
При теоретическом анализе удобнее использовать методы теории определителей, позволяющие записать решения в компактной форме. Прежде чем обращаться к этим методам, дадим основные понятия теории определителей.
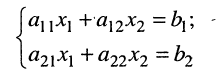
с неизвестными 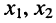
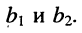
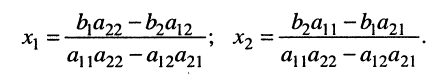
Стоящее в знаменателях полученных дробей выражение 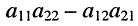
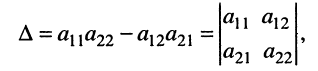
где вертикальные чёрточки являются знаком определителя. С помощью этого обозначения формулы (5.13) можно записать в виде
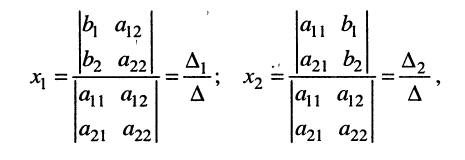
где 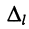
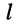
Из соотношений (5.14) следует: каждая из неизвестных 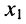
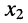
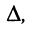
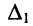
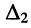
Подобным образом решается система уравнений любого порядка. Остаётся выяснить, как вычислять определители, если их порядок больше двух.
Рассмотрим вычисление определителя на примере системы третьего порядка:
решение которой приводит к дробям вида (5.12), где в знаменателе оказывается выражение
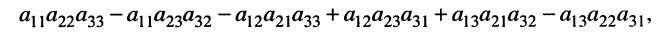
называемое определителем третьего порядка и обозначаемое
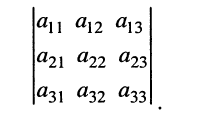
Применяя к (5.16) выражение (5.15), запишем определитель (5.16) в более удобной и наглядной форме:
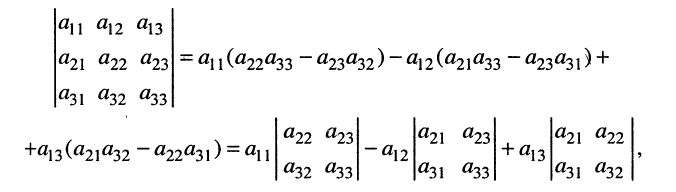
по которой можно вычислять значение определителя третьего порядка. Нетрудно видеть, что правая часть равенства состоит из суммы произведений коэффициентов (элементов) первой строки и определителей второго порядка с нужными знаками. Эти определители называются минорами и получаются из исходного определителя вычёркиванием первой строки и соответствующего данному элементу столбца. Например, минор относительно элемента 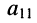
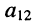
Подобные разложения можно произвести относительно элементов любой строки, предварительно записав соответствующие миноры.
Определение:
Минором 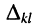
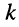
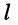
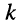
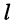
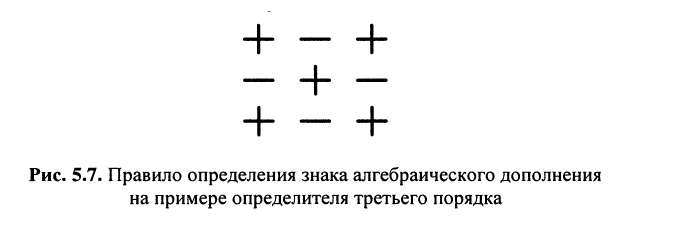
Знак минора определяется по формуле 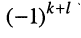
Определение:
Алгебраическим дополнением 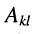
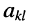
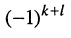
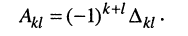
Из сказанного следует: определитель равен сумме произведений элементов какого-нибудь из рядов (строки или столбца) на алгебраические дополнения этих элементов.
При вычислении определителей больших порядков их предварительно разлагают на алгебраические дополнения. Отметим также, что подобно (5.14) для любой системы, у которой 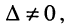
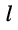
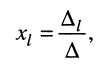
т. е. каждая 
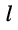
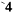
Применение теории определителей для решения контурных (узловых) уравнений
Применяя методы теории определителей к системе контурных уравнений (5.9), по формуле Крамера находим решение для первого контурного тока
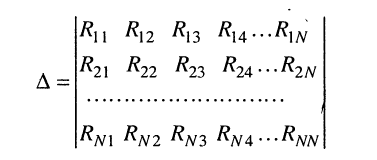
представляет собой определитель системы контурных уравнений (5.9), а
находится из определителя (5.20) при замене в нём первого столбца свободными членами. Заметим, что определитель (5.20) является симметричным относительно главной диагонали, поскольку 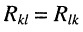
Разлагая определитель 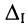
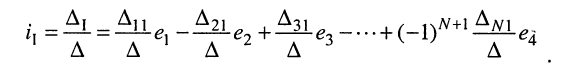
Аналогичное решение можно найти и для L-го контурного тока, разлагая определитель 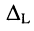
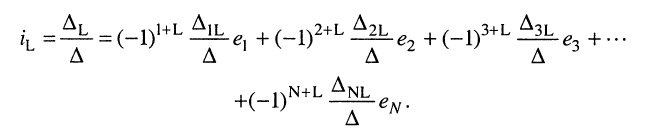
Полученное общее решение (5.22) системы контурных уравнений (5.9) показывает, что реакция в виде токов в электрической цепи представляет собой сумму реакций, вызываемых каждым из воздействий 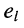
Аналогичным образом рассчитывается система узловых уравнений (5.2).
Примеры использования теории определителей
Задача 5.1.
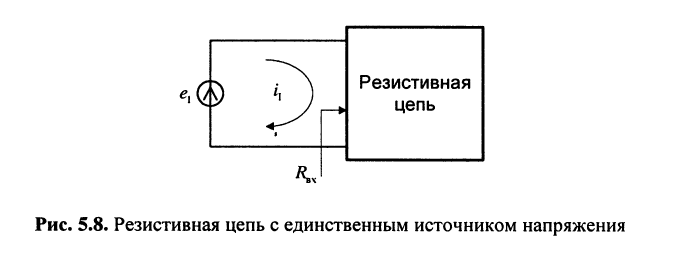
Цепь имеет единственный источник напряжения 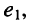
Решение. Для удобства назовём контур, замыкающийся через источник, первым. Тогда из (5.21) следует
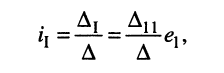
и согласно закону Ома имеем
откуда получаем соотношение
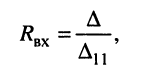
называемое входным сопротивлением двухполюсника. Оно представляет собой эквивалентное сопротивление пассивного резистивного двухполюсника.
Заметим, что в резистивном двухполюснике электрическая энергия может только рассеиваться, поэтому при выбранных на рис. 5.8 направлениях отсчёта тока и напряжения коэффициент 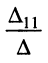
Задача 5.2.
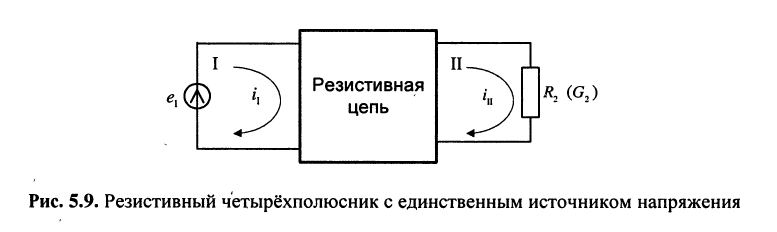
Найти ток в заданной ветви резистивной цепи (рис. 5.9), имеющей единственный источник напряжения в
Решение. Такую цепь можно рассматривать как резистивный четырёхполюсник, в котором вновь для удобства обозначим контур, содержащий источник напряжения, первым (I), а контур, содержащий интересующую нас ветвь, вторым (II).
При выбранных направлениях отсчёта ЭДС источника 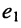
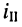
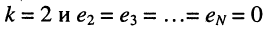
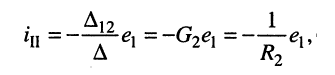
представляет собой собственное сопротивление второго контура и потому эквивалентное сопротивление четырёхполюсника.
Метод контурных токов
При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.
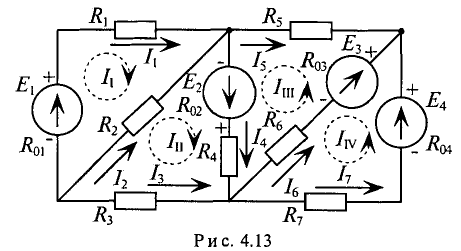
Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений
Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.
Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 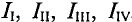
Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.
Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).
Для данной схемы (рис. 4.13) необходимо составить 4 уравнений. Со знаком «плюс» записываются ЭДС и падения напряжено разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные проконтурного тока.
Система уравнений для схемы (рис. 4.13):
Решением системы уравнений вычисляются значения контур-токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).
Пример 4.11
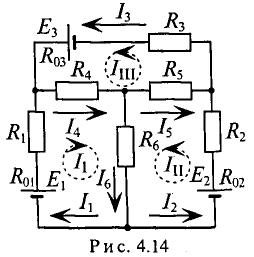
Определить токи во всех участках сложной цепи (рис. 4.14), если:
Решение
Необходимо составить 3 уравнения по второму закону для определения контурных токов 1 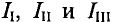
Подставляются числовые значения величин
Из уравнения (2) определяется ток
Значение тока 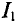
То же значение тока 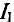
Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим
Откуда контурный ток
Из уравнения (3) определяется контурный ток
Из уравнения (2′) определяется ток
Вычисляются реальные токи в заданной цепи:
Проверяется правильность решения для 1 -го контура (рис. 4.14).
Такую же проверку можно произвести и для других контуров (2-го и 3-го):
Проверка показала правильность решения.
Определение метода контурных токов
Данный метод является фундаментальным и применим для расчета любых электрических цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, в каждом из них произвольно выбираются направления контурных токов и составляются уравнения по второму закону Кирхгофа. Для цепи по рис. 3.1 имеем:
Введем в полученную систему уравнений обобщенные параметры:
собственное сопротивление контура — сумма сопротивлений, входящих в состав контура, например, для первого контура:
смежные сопротивления — сопротивления на границах контуров, например, 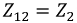
Тогда система уравнений примет вид:
Используя матричный метод расчета, можем записать:
В уравнении (3.8) 
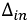
Токи ветвей, находящихся на границах контуров:
Справочный материал по методу контурных токов
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурное токи, замыкающиеся в контурах.
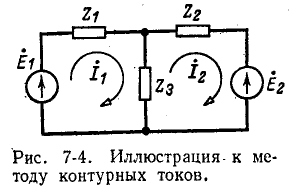
На рис. 7-4 в виде примера показана двухконтурная электрическая цепь, в которой 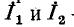
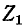
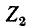
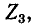
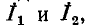
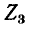
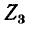
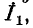
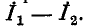
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р — q + I уравнений. Так, в схеме рис. 7-4 q = 2, р = 3; следовательно, число уравнений равно 3 — 2+1=2 (число независимых контуров).
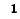
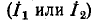
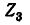
Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам, — общим сопротивлением этих контуров.
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 7-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис. 7-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:,
где 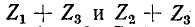
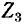
Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений: 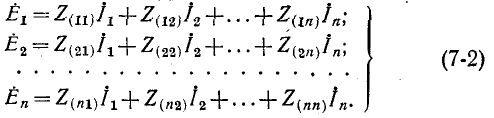
Здесь 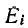
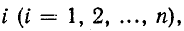
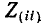
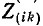
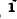
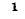
В соответствии со сказанным ранее собственные сопротивления 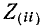
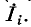
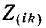
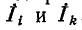
Решение уравнений (7-2) относительно искомых контурных токов может быть найдено с помощью определителей:
ит. д., где определитель системы
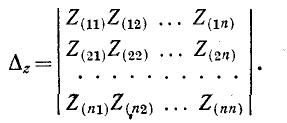
Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде 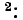
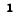
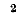
Здесь Дitl — алгебраическое дополнение элемента Z 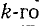
Сокращенно система уравнений (7-3) записывается в виде: 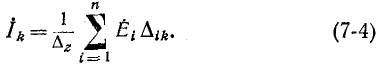
Первый индекс алгебраического дополнения i, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс 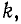
Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники э. д. с. При наличии в электрической схеме источников тока они могут быть заменены эквивалентными источниками э. д. с.
Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократятся на число заданных токов.
Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).
Электрические цепи могут быть планарными или непланарными.
Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с непере-крещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом Принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 7-5.
Электрическая цепь, приведенная на рис. 7-5, а, планарна, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 7-5, б.
Не планарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещиваю-щимися ветвями. Примером такой электрической цепи служит приведенная на рис. 7-5, в непланарная цепь, пересечение ветвей в которой не может быть устранено.
Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи смежных контуров
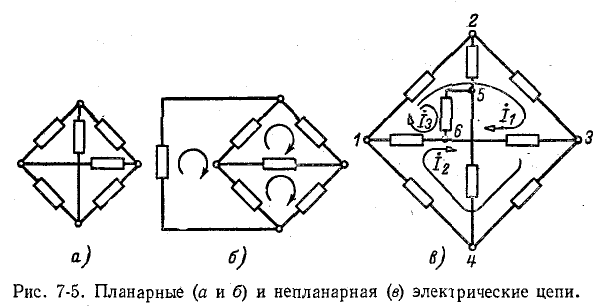
направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки'(см. пример 7-2). Это правило, однако, не является обязательным.
В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 7-5, в.
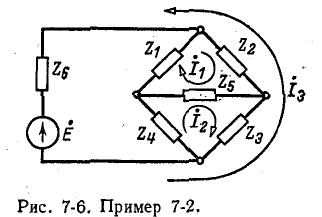
Пример 7-2.
Пользуясь методом контурных токов, определить ток в диагонали бюстовой схемы рис. 7-6.
Выбранные положительные направления контурных токов 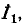
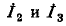
Решение полученной системы уравнений относительно контурных токов 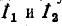
где М имеет то же значение, что и в примере 7-1.
Искомый ток в диагонали мостовой схемы равен разности контурных токов:
что совпадает с полученным в примере 7-1 ответом.
Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через ветвь 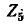
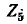
задача сведется к нахождению только одного контурного тока (вместо двух).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Метод контурных токов для расчёта электрических цепей
При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов позволяет уменьшить количество решаемых уравнений.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
В методе контурных токов уравнения составляются на основании второго закона Кирхгофа, причём их равно $ N_<\textrm<в>>-N_<\textrm<у>>+1 $, где $ N_<\textrm<у>> $ – число узлов, $ N_<\textrm<в>> $ – число ветвей, т.е. количество совпадает с количеством уравнений, составляемых по второму закону Кирхгофа.
Опишем методику составления уравнений по методу контурных токов. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
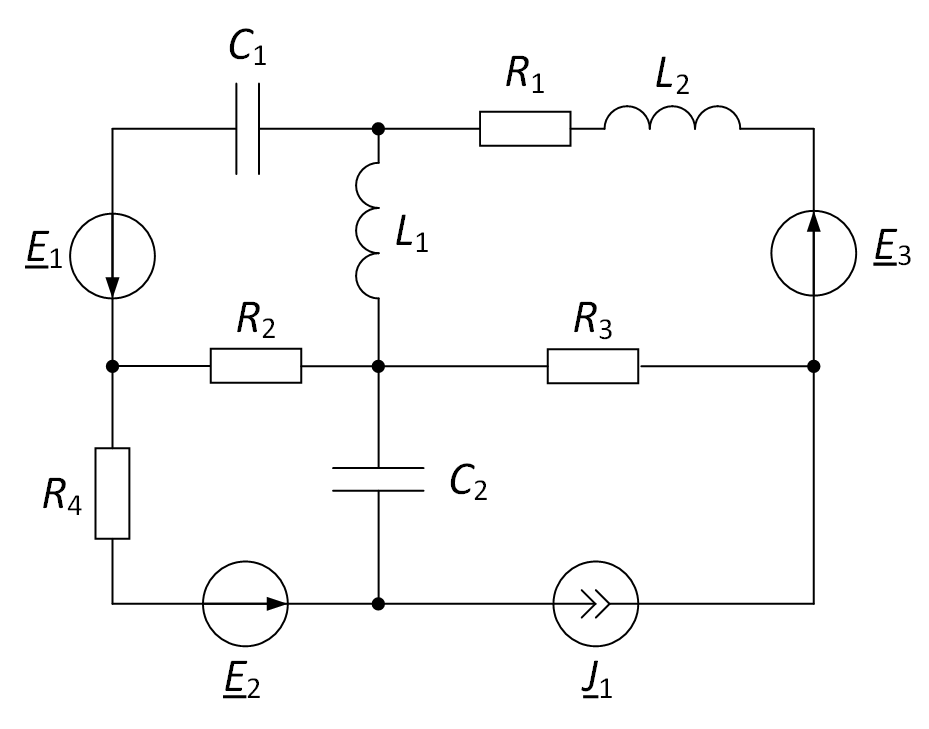
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно направления контурных токов (рис. 2).
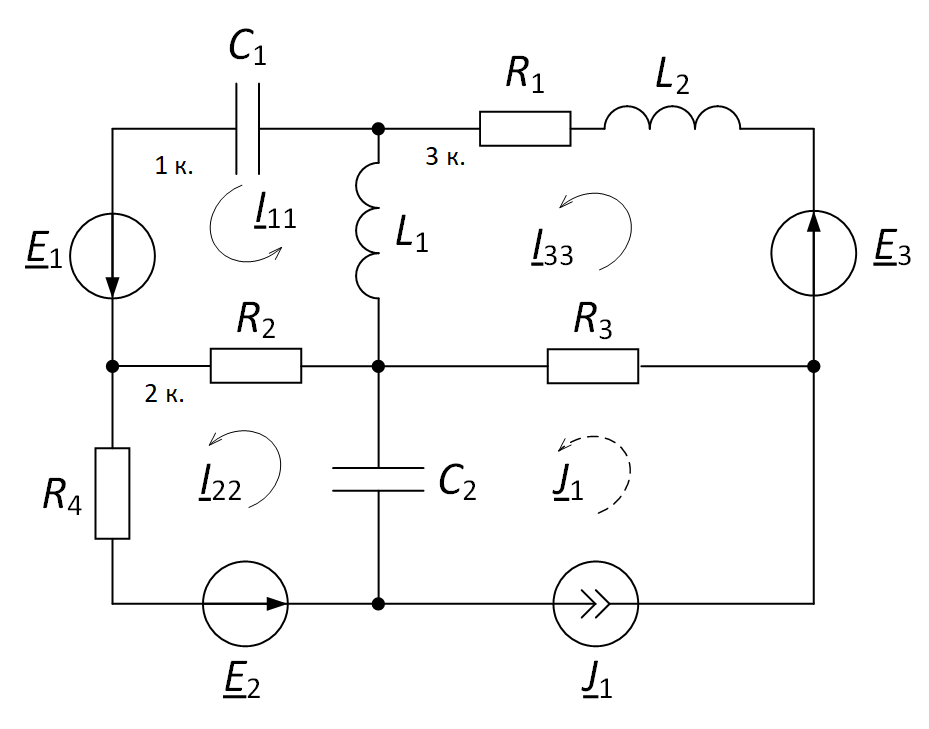
Рис. 2. Задание направления контурных токов в электрической цепи
Количество уравнений, составляемых по методу контурных токов, равно 3. Здесь контур с источником тока так же не рассматривается.
Составим уравнение для контура «1 к.». В контуре «1 к.» контурный ток $ \underline_ <11>$ протекает по всем сопротивлениям $ R_ <2>$, $ \underline
Учитывая вышеизложенное, уравнение по методу контурных токов для контура «1 к.» будет выглядеть следующим образом:
$$ (R_ <2>+ \underline
Аналогично составим уравнение для контура «2 к.». Необходимо учесть, что уравнение для контура с источником тока не составляется, но ток от источника тока также необходимо учитывать в уравнение аналогично контурным токам других контуров. Само уравнение будет выглядеть следующим образом:
$$ -R_ <2>\cdot \underline_ <11>+ (R_ <2>+ R_ <4>+ \underline
Для контура «3 к.»:
$$ -\underline
В приведённых выше уравнениях $ \underline
Таким образом, для того, чтобы найти искомые контурные токи, необходимо решить следующую систему уравнений, где слагаемые с силой тока источника тока перенесены в правую часть уравнений:
$$ \begin
В данном случае это система из 3 уравнений с 3 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
$$ \begin
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
В результате получим вектор-столбец $ \underline<\bold> $ токов из трёх элементов, состоящий из искомых контурных токов, при этом
Далее в схеме по рис. 2 расставим направления токов в ветвях (рис. 3).
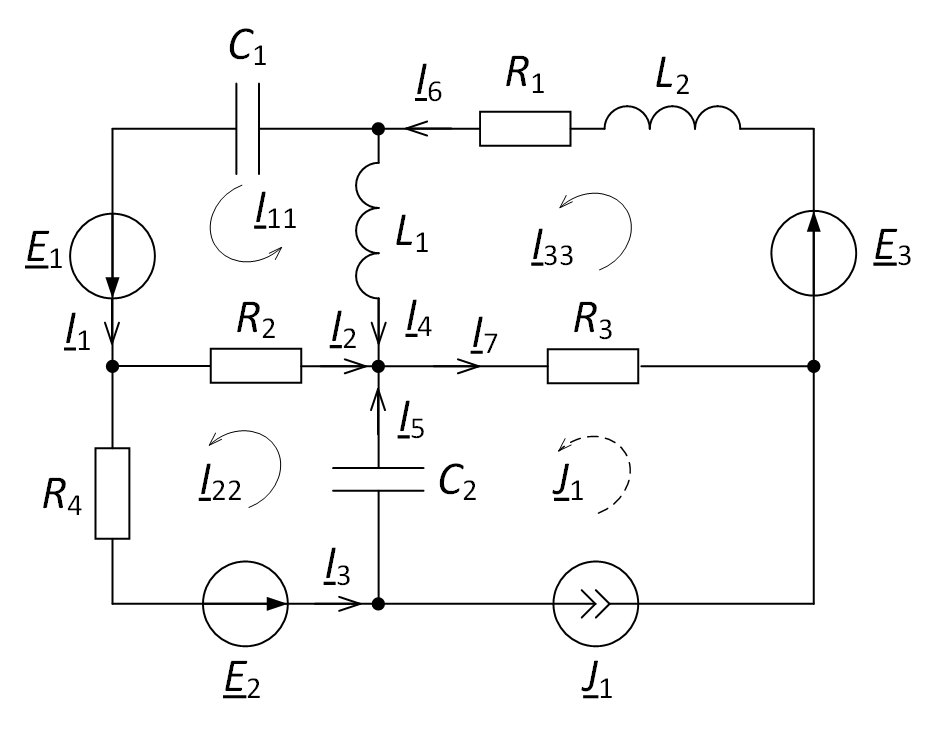
Рис. 3. Задание направления токов в электрической цепи
Для определения токов в ветвях необходимо рассмотреть все контурные токи, которые протекают через данную ветвь. Видим, что через ветвь, где протекает ток $ \underline_ <1>$, проходит только один контурный ток $ \underline_ <11>$, и он сонаправлен, отсюда
Через ветвь, где протекает ток $ \underline_ <2>$, проходят контурные токи $ \underline_ <11>$ и $ \underline_ <22>$, причём ток $ \underline_ <11>$ совпадает с принятым направлением тока $ \underline_ <2>$, а ток $ \underline_ <22>$ – не совпадает. Те контурные токи, которые совпадают с принятым направлением, берутся со знаком «+», те, которые не совпадают – со знаком «-». Отсюда
Аналогично для других ветвей
$$ \underline_ <5>= \underline_<22>— \underline
$$ \underline_ <7>= \underline_<33>— \underline
Итак, метод контурных токов позволяет рассчитывать меньшее количество сложных уравнений для расчёта аналогичной электрической цепи по сравнению с законами Кирхгофа.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…
Во время работы электроэнергетических систем могут возникнуть не только режимы коротких замыканий, но и обрывы. Метод…
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие…
Контурные уравнения для расчёта установившегося режима
Метод контурных уравнений предназначен для расчёта параметров установившихся режимов сложнозамкнутых электрических сетей. Суть метода заключается в составлении и решении системы контурных уравнений и определении на их основе параметров режима. Система контурных уравнений может быть записана в форме токов или мощностей. Число независимых контурных уравнений соответствует числу независимых контуров схемы. Составление контурных уравнений опирается на использование I и II законов Кирхгофа.
Содержание
Вывод уравнений в случае задания нагрузок токами
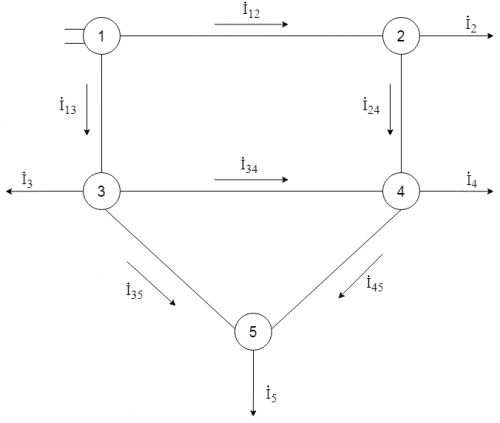
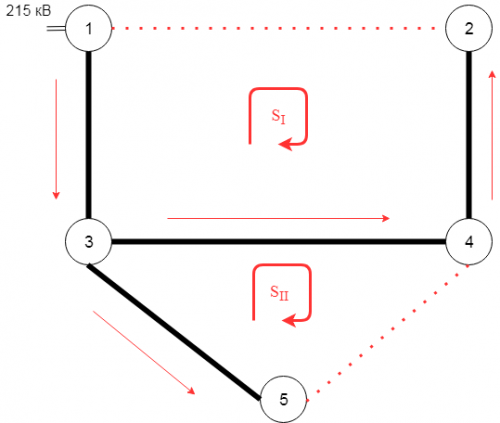
Рассмотрим вывод уравнений на примере схемы электрической сети, представленной на рисунке 1.
Запишем I закон Кирхгофа для всех узлов:
узел 2: [math] — \dot I_ <12>+ \dot I_2 + \dot I_ <24>= 0 [/math] (1) узел 3: [math] — \dot I_ <13>+ \dot I_3 + \dot I_ <34>+ \dot I_ <35>= 0 [/math] (2) узел 4: [math] — \dot I_ <34>— \dot I_ <24>+ \dot I_ <4>+ \dot I_ <45>= 0 [/math] (3) узел 5: [math] — \dot I_ <35>— \dot I_ <45>+ \dot I_ <5>= 0 [/math] (4)
для первого узла не имеет смысла записывать I закон Кирхгофа, так как первый узел является балансирующим.
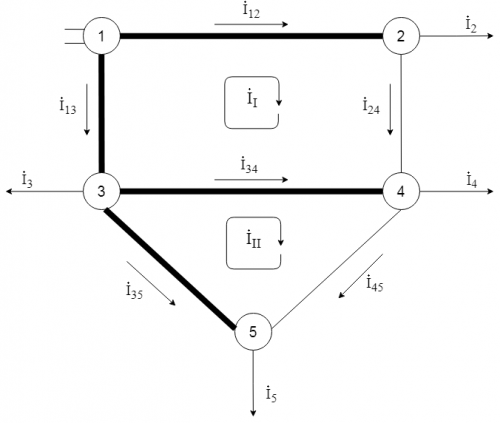
Обозначим остовное дерево графа сети и направление контурных токов, как показано на рисунке 2.
На рисунке 2 жирными линиями обозначено остовное дерево графа сети, тонкими линиями хорды.
Для удобства составления контурных уравнений рекомендуется выбирать остовное дерево так, чтобы между контурами были только рёбра графа, входящие в остовное дерево. Другими словами хорды графа должны быть с краёв графа сети. В приведённом примере графа сети не рекомендуется брать в качестве хорды ветвь 3-4, так как это приведёт к тому, что один из двух контуров будет вложен в другой. В свою очередь это увеличит количество слагаемых в контурных уравнений.
Значения контурных токов равны значениям токов ветвей, не входящих в состав дерева, поэтому:
[math]\dot I_ = \dot I_ <24>[/math] (5), и [math]\dot I_
Для удобства будем называть токи [math]\dot I_<2>, \dot I_<3>, \dot I_<4>, \dot I_<5>[/math] — узловые токи,
а [math]\dot I_<12>, \dot I_<13>, \dot I_<24>, \dot I_<34>, \dot I_<35>, \dot I_<45>[/math] — межузловые токи.
Далее, необходимо выразить все межузловые токи через контурные или узловые токи, не забывая про соотношения (5) и (6). Отсюда получаем:
[math]\dot I_ <12>= \dot I_+\dot I_ <2>[/math] , (7) [math]\dot I_ <13>= \dot I_<3>+\dot I_<35>+\dot I_ <34>[/math] , (8) [math]\dot I_ <35>= \dot I_<5>-\dot I_
Подставляем выражения (9) и (10) в (8), получаем:
[math]\dot I_ <13>= \dot I_<3>+\dot I_<4>+\dot I_<5>-\dot I_ [/math] , (11)
Запишем II закон Кирхгофа для двух контуров в виде системы:
[math]\displaystyle \begin
Воспользуемся законом Ома, согласно которому [math]\dot U_
Запишем систему уравнений (12), используя соотношение (13):
[math]\displaystyle \begin
Теперь, используя соотношения (7)-(11), то есть, записывая межузловые токи через контурные или узловые токи, запишем новую систему уравнений:
[math]\displaystyle \begin
Сгруппировав относительно [math]\dot I_[/math] и [math]\dot I_
[math]\displaystyle \begin
Пояснение к вышеобозначенной системе (16).
Множитель тока [math]\dot I_[/math] в первом уравнении (16.1) является собственным сопротивлением первого контура, включает в себя сумму сопротивлений всех ветвей, входящих в данный контур. Обозначается [math]\underline Z_
Исходя из вышесказанного, систему (16) можно представить в более наглядном виде:
[math]\displaystyle \begin
Контурные уравнения в форме баланса мощностей
Представим токи через соответствующие мощность и напряжение:
Подставим выражение (18) в систему (17), переобозначим свободную составляющую как [math] B_[/math] и [math] B_
Домножим каждое уравнение системы (19) на [math]\hat U[/math] , получим:
[math]\displaystyle \begin
Взяв сопряжение от каждого уравнения системы (20), мы получаем систему контурных уравнений в форме баланса мощностей:
[math]\displaystyle \begin
Пример расчёта потокораспределения в сети методом контурных уравнений
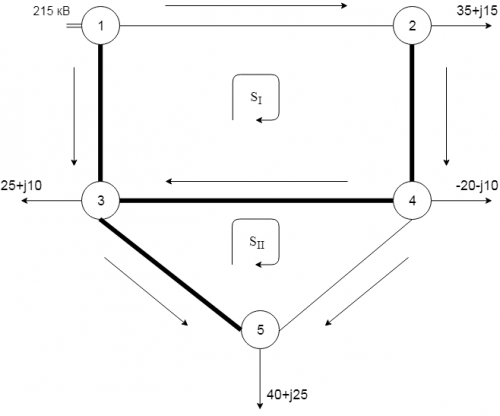
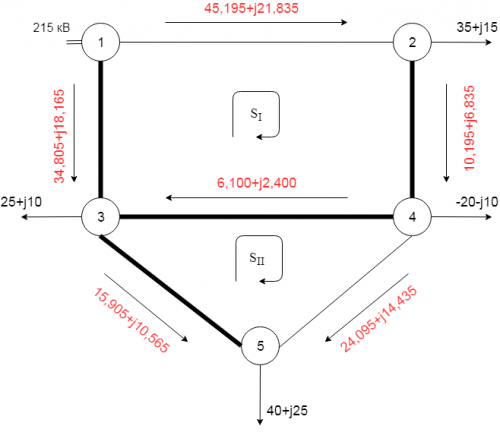
Для сети (рис. 3) расчитать потокораспределение без учёта потерь мощности методом контурных уравнений.
[math]\dot S_<2>=35+j15[/math] МВА, [math]\dot S_<3>=25+j10[/math] МВА, [math]\dot S_<4>=-20-j10[/math] МВА, [math]\dot S_<5>=40+j25[/math] МВА, [math]\underline Z_<12>=5+j17[/math] Ом, [math]\underline Z_<24>=4+j16[/math] Ом, [math]\underline Z_<34>=5+j19[/math] Ом, [math]\underline Z_<13>=8+j30[/math] Ом, [math]\underline Z_<35>=7+j26[/math] Ом, [math]\underline Z_<45>=6+j22[/math] Ом.
Запишем систему следующего вида:
[math]\displaystyle \begin
Для записи выражений свободных составляющих [math]\dot B_[/math] и [math]\dot B_
[math]\dot B_=-\hat
Решив данную систему уравнений относительно [math]\dot S_[/math] и [math]\dot S_
Мощность, протекающая по хорде (ветви, невходящей в состав дерева) равна соответствующей контурной мощности, поэтому
[math]\dot S_=\dot S_<12>=45,195+j21,835[/math] МВА, [math]\dot S_
Теперь найдем оставшиеся перетоки по ветвям, используя I закон Кирхгофа:
[math]\dot S_<24>=\dot S_<12>-\dot S_<2>=45,195+j21,835-(35+j15)=10,195+j6,835[/math] МВА, [math]\dot S_<43>=\dot S_<24>-\dot S_<4>-\dot S_<45>=10,195+j6,835-(-20-j10)-(24,095+j14,435)=6,100+j2,400[/math] МВА, [math]\dot S_<35>=\dot S_<5>-\dot S_<45>=40+j25-(24,095+j14,435)=15,905+j10,565[/math] МВА, [math]\dot S_<13>=\dot S_<3>+\dot S_<35>-\dot S_<43>=25+j10+15,905+j10,565-(6,100+j2,400)=34,805+j18,165[/math] МВА.
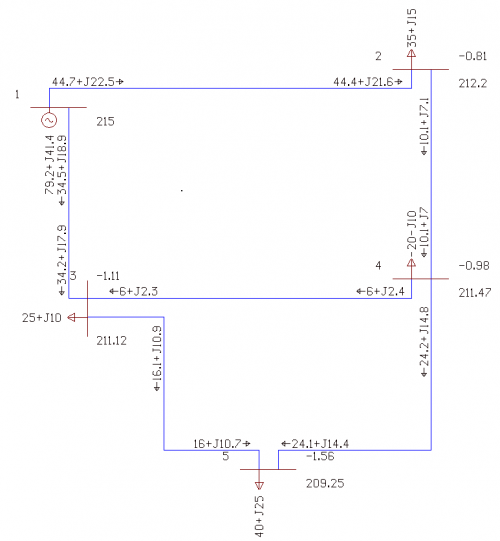
Проверка. Получившиеся значения перетоков по ветвям, исходящим из базы, должны равняться сумме мощностей узлов нагрузок.
[math]\dot S_<13>+\dot S_<12>=34,805+j18,165+45,195+j21,835=80+j40[/math] МВА, [math]\dot S_<2>+\dot S_<3>+\dot S_<4>+\dot S_<5>=35+j15+25+j10+(-20-j10)+40+j25=80+j40[/math] МВА.
http://faultan.ru/simulation/toe/loop_currents/
http://powersystem.info/index.php?title=%D0%9A%D0%BE%D0%BD%D1%82%D1%83%D1%80%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F_%D0%B4%D0%BB%D1%8F_%D1%80%D0%B0%D1%81%D1%87%D1%91%D1%82%D0%B0_%D1%83%D1%81%D1%82%D0%B0%D0%BD%D0%BE%D0%B2%D0%B8%D0%B2%D1%88%D0%B5%D0%B3%D0%BE%D1%81%D1%8F_%D1%80%D0%B5%D0%B6%D0%B8%D0%BC%D0%B0
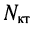
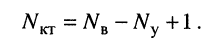
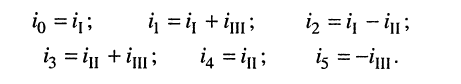
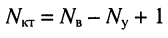 независимых контуров;
независимых контуров;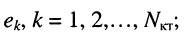
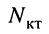 независимых контуров непосредственно связаны друг с другом, т. е. для к-го и 1-го контуров имеется хотя бы один элемент
независимых контуров непосредственно связаны друг с другом, т. е. для к-го и 1-го контуров имеется хотя бы один элемент 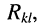 который входит в оба эти контура, причём
который входит в оба эти контура, причём 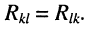
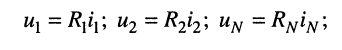
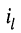 — ток в
— ток в 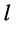 -ой ветви;
-ой ветви;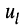 — напряжение в
— напряжение в 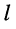 -ой ветви;
-ой ветви;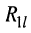 — сопротивление элемента, общего для 1-го и
— сопротивление элемента, общего для 1-го и 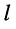 -го контуров.
-го контуров.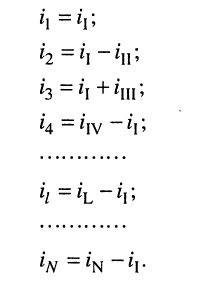
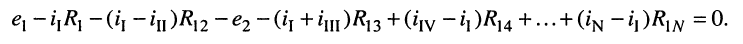
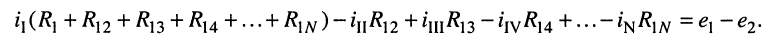
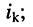
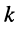 -го контура, для которого составляется уравнение, представляет собой арифметическую сумму сопротивлений этого контура;
-го контура, для которого составляется уравнение, представляет собой арифметическую сумму сопротивлений этого контура;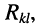 общего для
общего для 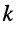 -го и
-го и 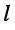 -го контуров, на контурный ток 1-го контура; эти слагаемые входят в уравнение со знаком «+», если направления токов
-го контуров, на контурный ток 1-го контура; эти слагаемые входят в уравнение со знаком «+», если направления токов 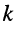 -го и
-го и 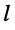 -го контуров в элементе
-го контуров в элементе 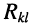 совпадают; в противном случае они входят в уравнение с отрицательным знаком.
совпадают; в противном случае они входят в уравнение с отрицательным знаком.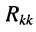 — собственное сопротивление k-го контура, оно определяется как арифметическая сумма сопротивлений всех элементов
— собственное сопротивление k-го контура, оно определяется как арифметическая сумма сопротивлений всех элементов 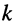 -го контура;
-го контура;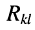 — взаимное сопротивление
— взаимное сопротивление 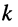 -го и
-го и 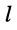 -го контуров цепи
-го контуров цепи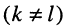 , оно является сопротивлением элемента, общего для
, оно является сопротивлением элемента, общего для 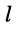 -го контуров; слагаемые вида
-го контуров; слагаемые вида 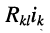 входят со знаком «+» при совпадении направлений токов в этих контурах; если связь между
входят со знаком «+» при совпадении направлений токов в этих контурах; если связь между 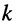 -ым и
-ым и 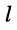 -ым контурами осуществляется через несколько элементов активного сопротивления, то
-ым контурами осуществляется через несколько элементов активного сопротивления, то 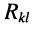 представляет собой арифметическую сумму соответствующих взаимных сопротивлений, причём
представляет собой арифметическую сумму соответствующих взаимных сопротивлений, причём 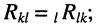
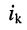 — контурный ток
— контурный ток 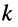 -го контура цепи;
-го контура цепи;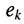 — контурная ЭДС
— контурная ЭДС 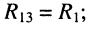
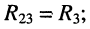
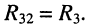
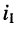 совпадает с направлением контурного тока
совпадает с направлением контурного тока 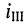 и противоположно направлению контурного
и противоположно направлению контурного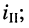
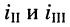 совпадают;
совпадают;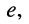 а два других контура источников не имеют.
а два других контура источников не имеют.