Область определения функции
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Материал со звездочкой
Старшеклассникам нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
- Через точку с запятой указываем два числа: левую и правую границы промежутка.
- Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую.
- Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞.
- Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
- Областью определения функции y = 3 √9 является множество R.
Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
- Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
- Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x 2 + 4x + 3 > 0.
Для этого решим квадратное уравнение x 2 + 4x + 3 = 0. Находим дискриминант:
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола f(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x 2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x 2 + 4x + 3
Область определения степенной функции
Степенная функция выглядит так: y = x a , то есть, f(x) = x a , где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = x a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0 0 . А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x 5 , y = x 12 — множество R, так как показатели степени целые положительные.
- Степенные функции
определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x −2 , как и функции y = x −5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x -√19 , y = x -3e ,
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
Область определения показательной функции
Показательную функцию можно задать формулой y = a x , где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
- y = e x
- y = (√15) x
- y = 13 x .
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
- y = log7x
- y = lnx
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
- Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
- Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].
Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.
Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].
Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y = x + x — 2 или y = 5 · x 2 + 1 · x 3 , y = x x — 5 или y = x — 1 5 — 3 . Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть ( 0 , + ∞ ) или такой [ − 3 , 1 ) ∪ [ 5 , 7 ) . Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y = x + 2 · x x 4 — 1 ;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y = x + 1 или y = 2 3 · x + 3 x ;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y = 5 · ( x + 1 ) — 3 , y = — 1 + x 1 1 3 , y = ( x 3 — x + 1 ) 2 , которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y = ln x 2 + x 4 или y = 1 + log x — 1 ( x + 1 ) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y = x 3 + t g 2 · x + 5 или y = c t g ( 3 · x 3 — 1 ) , так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y = a r c sin ( x + 2 ) + 2 · x 2 , y = a r c cos x — 1 + x , область определения которых определяется ни интервале от — 1 до 1 .
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y = x 4 + 2 · x 2 — x + 1 2 + 2 2 3 · x . Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y = 2 · x + 1 . Для вычисления ее значения можем определить x . Из выражения 2 · x + 1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y = 3 x — 1 , а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3 x — 1 знаменатель равняется нулю при х = 1 , поэтому искомая область определения данной функции примет вид ( − ∞ , 1 ) ∪ ( 1 , + ∞ ) и считается числовым множеством.
На рассмотрении примера y = x 2 — 5 · x + 6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x 2 − 5 · x + 6 ≥ 0 . После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как ( − ∞ , 2 ] ∪ [ 3 , + ∞ ) .
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция f f считается суммой n функций f 1 , f 2 , … , f n , иначе говоря, эта функция задается при помощи формулы y = f 1 ( x ) + f 2 ( x ) + … + f n ( x ) , тогда ее область определения считается пересечением областей определения функций f 1 , f 2 , … , f n . Данное утверждение можно записать как:
D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Заданная функция представляется как сумма четырех: степенной с показателем 7 ,степенной с показателем 1 , постоянной, функции тангенса.
По таблице определения видим, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) , D ( f 3 ) = ( − ∞ , + ∞ ) , причем область определения тангенса включает в себя все действительные числа, кроме π 2 + π · k , k ∈ Z .
Областью определения заданной функции f является пересечение областей определения f 1 , f 2 , f 3 и f 4 . То есть для функции существует такое количество действительных чисел, куда не входит π 2 + π · k , k ∈ Z .
Ответ: все действительные числа кроме π 2 + π · k , k ∈ Z .
Для нахождения области определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f 1 , f 2 , f 3 и f n , тогда существует такая функция f , которую можно задать при помощи формулы y = f 1 ( x ) · f 2 ( x ) · … · f n ( x ) , тогда ее область определения считается областью определения для всех функций.
Запишется D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Найти область определения функции y = 3 · a r c t g x · ln x .
Правая часть формулы рассматривается как f 1 ( x ) · f 2 ( x ) · f 3 ( x ) , где за f 1 является постоянной функцией, f 2 является арктангенсом, f 3 – логарифмической функцией с основанием e . По условию имеем, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) и D ( f 3 ) = ( 0 , + ∞ ) . Мы получаем, что
D ( f ) = D ( f 1 ) D ( f 2 ) D ( f n ) = ( — ∞ , + ∞ ) ( — ∞ , + ∞ ) D ( 0 , + ∞ ) = ( 0 , + ∞ )
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y = C · f ( x ) , где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y = C · f ( x ) – произведение постоянной функции и f . Область определения – это все действительные числа области определения D ( f ) . Отсюда видим, что область определения функции y = C · f ( x ) является — ∞ , + ∞ D ( f ) = D ( f ) .
Получили, что область определения y = f ( x ) и y = C · f ( x ) , где C является некоторое действительное число, совпадают. Это видно на примере определения корня y = x считается [ 0 , + ∞ ) , потому как область определения функции y = — 5 · x — [ 0 , + ∞ ) .
Области определения y = f ( x ) и y = − f ( x ) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y = log 3 x − 3 · 2 x .
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
f 1 ( x ) = log 3 x и f 2 ( x ) = 3 · 2 x . Тогда получим, что D ( f ) = D ( f 1 ) D ( f 2 ) .
Область определения записывается как D ( f 1 ) = ( 0 , + ∞ ) . Приступим к области определения f 2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D ( f 2 ) = ( − ∞ , + ∞ ) .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
D ( f ) = D ( f 1 ) D ( f 2 ) = ( 0 , + ∞ ) — ∞ , + ∞
Необходимо озвучить утверждение о том, что областью определения y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 является множество действительных чисел.
Рассмотрим y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы ( n + 1 ) -ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R .
Найти область определения f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 .
Примем обозначение f за разность двух функций, тогда получим, что f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 и f 2 ( x ) = 3 · x — ln 5 . Выше было показано, что D ( f 1 ) = R . Область определения для f 2 является совпадающей со степенной при показателе – ln 5 , иначе говоря, что D ( f 2 ) = ( 0 , + ∞ ) .
Получаем, что D ( f ) = D ( f 1 ) D ( f 2 ) = — ∞ , + ∞ ( 0 , + ∞ ) = ( 0 , + ∞ ) .
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y = f 1 ( f 2 ( x ) ) . Известно, что D ( f ) является множеством всех x из определения функции f 2 , где область определения f 2 ( x ) принадлежит области определения f 1 .
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Найти область определения y = ln x 2 .
Данную функцию представляем в виде y = f 1 ( f 2 ( x ) ) , где имеем, что f 1 является логарифмом с основанием e , а f 2 – степенная функция с показателем 2 .
Для решения необходимо использовать известные области определения D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) .
Тогда получим систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — ∞ , + ∞ x 2 ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x 2 > 0 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ )
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Найти область определения функции y = ( a r c sin x ) — 1 2 .
Так как дана сложная функция, необходимо рассматривать ее как y = f 1 ( f 2 ( x ) ) , где f 1 является степенной функцией с показателем — 1 2 , а f 2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = [ − 1 , 1 ] . Теперь найдем все множества значений x , где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . Получаем систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — 1 , 1 a r c sin x ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ — 1 , 1 a r c sin x > 0
Для решения a r c sin x > 0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [ − 1 , 1 ] , причем обращается в ноль при х = 0 , значит, что a r c sin x > 0 из определения x принадлежит промежутку ( 0 , 1 ] .
Преобразуем систему вида
x ∈ — 1 , 1 a r c sin x > 0 ⇔ x ∈ — 1 , 1 x ∈ ( 0 , 1 ] ⇔ x ∈ ( 0 , 1 ]
Область определения искомой функции имеет интервал равный ( 0 , 1 ] .
Ответ: ( 0 , 1 ] .
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y = f 1 ( f 2 ( … f n ( x ) ) ) ) . Область определения такой функции ищется из x ∈ D ( f n ) f n ( x ) ∈ D ( f n — 1 ) f n — 1 ( f n ( x ) ) ∈ D ( f n — 2 ) . . . f 2 ( f 3 ( . . . ( f n ( x ) ) ) ∈ D ( f 1 ) .
Найти область определения y = sin ( l g x 4 ) .
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
Имеем, что по условию D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = [ 0 , + ∞ ) , D ( f 3 ) = ( 0 , + ∞ ) . Тогда областью определения функции – это пересечение множеств таких значений, где x ∈ D ( f 3 ) , f 3 ( x ) ∈ D ( f 2 ) , f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) . Получаем, что
x ∈ D ( f 3 ) f 3 ( x ) ∈ D ( f 2 ) f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞
Условие lg x 4 ∈ — ∞ , + ∞ аналогично условию l g x ∈ [ 0 , + ∞ ) , значит
x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ 0 ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ lg 1 ⇔ x ∈ ( 0 , + ∞ ) x ≥ 1 ⇔ ⇔ x ∈ [ 1 , + ∞ )
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f 1 ( x ) f 2 ( x ) . Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f 2 ( х ) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Запишем функцию y = f 1 ( x ) f 2 ( x ) в виде y = f 1 ( x ) · ( f 2 ( x ) ) — 1 . Тогда получим произведение функций вида y = f 1 ( x ) с y = ( f 2 ( x ) ) — 1 . Областью определения функции y = f 1 ( x ) является множество D ( f 1 ) , а для сложной y = ( f 2 ( x ) ) — 1 определим из системы вида x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Значит, x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Найти область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 .
Заданная функция дробная, поэтому f 1 – сложная функция, где y = t g ( 2 · x + 1 ) и f 2 – целая рациональная функция, где y = x 2 − x − 6 , а область определения считается множеством всех чисел. Можно записать это в виде
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Представление сложной функции y = f 3 ( f 4 ( x ) ) , где f 3 –это функция тангенс, где в область определения включены все числа, кроме π 2 + π · k , k ∈ Z , а f 4 – это целая рациональная функция y = 2 · x + 1 с областью определения D ( f 4 ) = ( − ∞ , + ∞ ) . После чего приступаем к нахождению области определения f 1 :
x ∈ D ( f 4 ) 2 · x + 1 ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) 2 x + 1 ≠ π 2 + π · k , k ∈ Z ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z
Еще необходимо рассмотреть нижнюю область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 . Тогда получаем, что
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ∈ — ∞ , + ∞ x 2 — x — 6 ≠ 0 ⇔ ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ≠ — 2 x ≠ 3
Ответ: множество действительных чисел, кроме — 2 , 3 и π 4 — 1 2 + π 2 · k , k ∈ Z .
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1 . Отсюда видно, что функция y = log f 2 ( x ) f 1 ( x ) имеет область определения, которая выглядит так:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 . После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y = log a f 1 ( x ) и y = log a f 2 ( x ) можно определить из получившейся системы вида x ∈ D ( f 1 ) f 1 ( x ) > 0 и x ∈ D ( f 2 ) f 2 ( x ) > 0 . Иначе эту область можно записать в виде y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 , что означает нахождение y = log f 2 ( x ) f 1 ( x ) из самой системы вида
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Обозначить область определения функции y = log 2 · x ( x 2 — 6 x + 5 ) .
Следует принять обозначения f 1 ( x ) = x 2 − 6 · x + 5 и f 2 ( x ) = 2 · x , отсюда D ( f 1 ) = ( − ∞ , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) . Необходимо приступить к поиску множества x , где выполняется условие x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1 . Тогда получаем систему вида
x ∈ ( — ∞ , + ∞ ) x 2 — 6 x + 5 > 0 x ∈ ( — ∞ , + ∞ ) 2 · x > 0 2 · x ≠ 1 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 1 ) ∪ ( 5 , + ∞ ) x ∈ ( — ∞ , + ∞ ) x > 0 x ≠ 1 2 ⇔ ⇔ x ∈ 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ )
Отсюда видим, что искомой областью функции y = log 2 · x ( x 2 — 6 x + 5 ) считается множнство, удовлетворяющее условию 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Ответ: 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y = ( f 1 ( x ) ) f 2 ( x ) . Ее область определения включает в себя такие значения x , которые удовлетворяют системе x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Эта область позволяет переходить от показательно-степенной к сложной вида y = a log a ( f 1 ( x ) ) f 2 ( x ) = a f 2 ( x ) · log a f 1 ( x ) , где где a > 0 , a ≠ 1 .
Найти область определения показательно-степенной функции y = ( x 2 — 1 ) x 3 — 9 · x .
Примем за обозначение f 1 ( x ) = x 2 − 1 и f 2 ( x ) = x 3 — 9 · x .
Функция f 1 определена на множестве действительных чисел, тогда получаем область определения вида D ( f 1 ) = ( − ∞ , + ∞ ) . Функция f 2 является сложной, поэтому ее представление примет вид y = f 3 ( f 4 ( x ) ) , а f 3 – квадратным корнем с областью определения D ( f 3 ) = [ 0 , + ∞ ) , а функция f 4 – целой рациональной, D ( f 4 ) = ( − ∞ , + ∞ ) . Получаем систему вида
x ∈ D ( f 4 ) f 4 ( x ) ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) x 3 — 9 · x ≥ 0 ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) ⇔ x ∈ — 3 , 0 ∪ [ 3 , + ∞ )
Значит, область определения для функции f 2 имеет вид D ( f 2 ) = [ − 3 , 0 ] ∪ [ 3 , + ∞ ) . После чего необходимо найти область определения показательно-степенной функции по условию x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Получаем систему вида x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x 2 — 1 > 0 ⇔ x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x ∈ ( — ∞ , — 1 ) ∪ ( 1 , + ∞ ) ⇔ ⇔ x ∈ — 3 , — 1 ∪ [ 3 , + ∞ )
Ответ: [ − 3 , − 1 ) ∪ [ 3 , + ∞ )
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Функция | Ее область определения |
| R | |
| Линейная y = k · x + b | R |
| — ∞ , 0 ∪ 0 , + ∞ | |
| Квадратичная y = a · x 2 + b · x + c | R |
| y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 | R |
| Целая рациональная | R |
| y = C · f ( x ) , где C — число | D ( f ) |
| y = f ( x ) n , где n — четное | x ∈ D ( f 1 ) , f ( x ) ≥ 0 |
| Показательно-степенная y = ( f 1 ( x ) ) f 2 ( x ) | x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 1 ( x ) > 0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y = x 2 — 4 x — 2 и y = x + 2 являются разными функциями, так как первая определяется на ( − ∞ , 2 ) ∪ ( 2 , + ∞ ) , а вторая из множества действительных чисел. Из преобразования y = x 2 — 4 x — 2 = x — 2 x + 2 x — 2 = x + 2 видно, что функция имеет смысл при x ≠ 2 .
Область значения функций в задачах ЕГЭ
Разделы: Математика
Понятие функции и всё, что с ним связано, относится к традиционно сложным, не до конца понятым. Особым камнем преткновения при изучении функции и подготовке к ЕГЭ являются область определения и область значений (изменения) функции.
Нередко учащиеся не видят разницы между областью определения функции и областью её значений.
И если задачи на нахождение области определения функции учащимся удаётся освоить, то задачи на нахождение множества значений функции вызывают у них немалые затруднения.
Цель данной статьи: ознакомление с методами нахождения значений функции.
В результате рассмотрения данной темы был изучен теоретический материал, рассмотрены способы решения задач на нахождение множеств значений функции, подобран дидактический материал для самостоятельной работы учащихся.
Данная статья может быть использована учителем при подготовке учащихся к выпускным и вступительным экзаменам, при изучении темы “Область значения функции” на факультативных занятиях элективных курсах по математике.
I. Определение области значений функции.
Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.
Напомним области значений основных элементарных функций.
| Функция | Множество значений |
| y = kx+ b | E(y) = (-∞;+∞) |
| y = x 2n | E(y) = [0;+∞) |
| y = x 2n +1 | E(y) = (-∞;+∞) |
| y = k/x | E(y) = (-∞;0)u(0;+∞) |
| y = x 1/2n | E(y) = [0;+∞) |
| y = x 1/2n+1 | E(y) = (-∞;+∞) |
| y = a x | E(y) = (0;+∞) |
| y = logax | E(y) = (-∞;+∞) |
| y = sin x | E(y) = [-1;1] |
| y = cos x | E(y) = [-1;1] |
| y = tg x | E(y) = (-∞;+∞) |
| y = ctg x | E(y) = (-∞;+∞) |
| y = arcsin x | E(y) = [-π/2 ; π/2] |
| y = arcos x | E(y) = [0; π] |
| y = arctg x | E(y) = (-π/2 ; π/2) |
| y = arcctg x | E(y) = (0; π) |
Заметим также, что областью значения всякого многочлена чётной степени является промежуток [m;+∞) , где m – наименьшее значение этого многочлена, либо промежуток
(-∞;n] , где n – наибольшее значение этого многочлена.
II. Свойства функций, используемые при нахождении области значений функции
Для успешного нахождения множества значений функции надо хорошо знать свойства основных элементарных функций, особенно их области определения, области значений и характер монотонности. Приведём свойства непрерывных, монотонных дифференцируемых функций, наиболее часто используемые при нахождении множества значений функций.
- Если функция f(x) непрерывна и возрастает на отрезке [a;b], то множество значений функции на этом отрезке есть отрезок [f(a),f(b)]. При этом каждое значение А
[f(a),f(b)] функция принимает ровно при одном значении x принадлежит [a,b], т.е уравнение f(x) = А имеет единственный корень на отрезке [a,b]. Если же f(x) – непрерывная и убывающая на отрезке [a,b] функция, то её множество значений на [a,b] есть отрезок [f(a),f(b)].
- Если функция f(x) непрерывна на отрезке [a,b] и m = min f(x), M = max f(x) – её наименьшее и наибольшее значение на этом отрезке, то множество значений f(x) на [a,b] есть отрезок [m;M].
- Если функция непрерывна на отрезке [a,b] и дифференцируема (имеет производную) в интервале (a,b), то наибольшее и наименьшее значения функции на отрезке [a,b] существуют и достигаются либо на концах отрезка, либо в критических точках функции, расположенных на отрезке
Свойства 2 и 3, как правило, используются вместе свойством элементарной функции быть непрерывной в своей области определения. При этом наиболее простое и краткое решение задачи на нахождение множества значений функции достигается на основании свойства 1, если несложными методами удаётся определить монотонность функции. Решение задачи ещё упрощается, если функция, вдобавок, – чётная или нечётная, периодическая и т.д. Таким образом, при решении задач на нахождение множеств значений функции следует по мере надобности проверять и использовать следующие свойства функции:
- непрерывность;
- монотонность;
- дифференцируемость;
- чётность, нечётность, периодичность и т.д.
Несложные задачи на нахождение множества значений функции в большинстве своём ориентированны:
а) на использование простейших оценок и ограничений: (2 х >0, -1≤sinx?1, 0≤cos 2 x?1 и т.д.);
б) на выделение полного квадрата: х 2 – 4х + 7 = (х – 2) 2 + 3;
в) на преобразование тригонометрических выражений: 2sin 2 x – 3cos 2 x + 4 = 5sin 2 x +1;
г) использование монотонности функции x 1/3 + 2 x-1 возрастает на R.
III. Рассмотрим способы нахождения областей значений функций.
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Раскроем суть этих методов на конкретных примерах.
Пример 1. Найдите область значений E(y) функции y = log0,5(4 – 2·3 x – 9 x ).
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
y = log0,5(5 – (1 + 2·3 x – 3 2x )) = log0,5(5 – (3 x + 1) 2 )
И последовательно найдём множества значений её сложных аргументов:
E(3 x ) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2 ) = (-∞;4)
Обозначим t = 5 – (3 x +1) 2 , где -∞≤t≤4. Тем самым задача сводится к нахождению множества значений функции y = log0,5t на луче (-∞;4). Так как функция y = log0,5t определена лишь при, то её множество значений на луче (-∞;4) совпадает со множеством значений функции на интервале (0;4), представляющем собой пересечение луча (-∞;4) с областью определения (0;+∞) логарифмической функции. На интервале (0;4) эта функция непрерывна и убывает. При t > 0 она стремится к +∞, а при t = 4 принимает значение -2, поэтому E(y) = (-2, +∞).
Пример 2. Найдите область значений функции
y = cos7x + 5cosx
Решим этот пример методом оценок, суть которого состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Из неравенств -1≤cos7x?1, -5≤5cosx?5 получим оценку -6≤y?6. При x = р и x = 0 функция принимает значения -6 и 6, т.е. достигает нижней и верхней границы оценки. Как линейная комбинация непрерывных функций cos7x и cosx, функция y непрерывна на всей числовой оси, поэтому по свойству непрерывной функции она принимает все значения с -6 до 6 включительно, и только их, так как в силу неравенств -6≤y?6 другие значения у неё невозможны. Следовательно, E(y) = [-6;6].
Пример 3. Найдите область значений E(f) функции f(x) = cos2x + 2cosx.
По формуле косинуса двойного угла преобразуем функция f(x) = 2cos 2 x + 2cosx – 1 и обозначим t = cosx. Тогда f(x) = 2t 2 + 2t – 1. Так как E(cosx) =
[-1;1], то область значений функции f(x) совпадает со множеством значений функции g(t) = 2t 2 + 2t – 1 на отрезке [-1;1], которое найдём графическим методом. Построив график функции y = 2t 2 + 2t – 1 = 2(t + 0,5) 2 – 1,5 на промежутке [-1;1], находим E(f) = [-1,5; 3].
Замечание – к нахождению множества значений функции сводятся многие задачи с параметром, связанные, в основном, с разрешимостью и числом решений уравнения и неравенств. Например, уравнение f(x) = а разрешимо тогда и только тогда, когда
a 

Пример 4. При каких значениях параметра а уравнение (x + 5) 1/2 = a(x 2 + 4) имеет единственный корень на отрезке [-4;-1].
Запишем уравнение в виде (x + 5) 1/2 / (x 2 + 4) = a . Последнее уравнение имеет хотя бы один корень на отрезке [-4;-1] тогда и только тогда, когда а принадлежит множеству значений функции f(x) = (x + 5) 1/2 / (x 2 + 4) на отрезке [-4;-1]. Найдём это множество, используя свойство непрерывности и монотонности функции.
На отрезке [-4;-1] функция y = xІ + 4 непрерывна, убывает и положительна, поэтому функция g(x) = 1/(x 2 + 4) непрерывна и возрастает на этом отрезке, так как при делении на положительную функцию характер монотонности функции меняется на противоположный. Функция h(x) = (x + 5) 1/2 непрерывна и возрастает в своей области определения D(h) = [-5;+∞) и, в частности на отрезке [-4;-1], где она, кроме того, положительна. Тогда функция f(x)=g(x)·h(x), как произведение двух непрерывных, возрастающих и положительных функций, также непрерывна и возрастает на отрезке [-4;-1], поэтому её множество значений на [-4;-1] есть отрезок [f(-4); f(-1)] = [0,05; 0,4]. Следовательно, уравнение имеет решение на отрезке [-4;-1], причём единственное (по свойству непрерывной монотонной функции), при 0,05 ≤ a ≤ 0,4
Замечание. Разрешимость уравнения f(x) = a на некотором промежутке Х равносильна принадлежности значений параметра а множеству значений функции f(x) на Х. Следовательно, множество значений функции f(x) на промежутке Х совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень на промежутке Х. В частности, область значений E(f) функции f(x)совпадает с множеством значений параметра а, для которых уравнение f(x) = a имеет хотя бы один корень.
Пример 5. Найдите область значений E(f) функции
Решим пример методом введения параметра, согласно которому E(f) совпадает с множеством значений параметра а, для которых уравнение
имеет хотя бы один корень.
При а=2 уравнение является линейным – 4х – 5 = 0 с ненулевым коэффициентом при неизвестной х , поэтому имеет решение. При а≠2 уравнение является квадратным, поэтому оно разрешимо тогда и только тогда, когда его дискриминант
Так как точка а = 2 принадлежит отрезку

Как непосредственное развитие метода введения параметра при нахождении множества значений функции, можно рассматривать метод обратной функции, для нахождения которой надо решить относительно х уравнение f(x)= y, считая y параметром. Если это уравнение имеет единственное решение x =g(y), то область значений E(f) исходной функции f(x) совпадает с областью определения D(g) обратной функции g(y). Если же уравнение f(x)= y имеет несколько решений x =g1(y), x =g2(y) и т.д., то E(f) равна объединению областей определений функции g1(y), g2(y) и т.д.
Пример 6. Найдите область значений E(y) функции y = 5 2/(1-3x).
найдём обратную функцию x = log3((log5y – 2)/(log5y)) и её область определения D(x):
Так как уравнения относительно х имеет единственное решение, то
E(y) = D(x) = (0; 1)
Если область определения функции состоит из нескольких промежутков или функция на разных промежутках задана разными формулами, то для нахождения области значений функции надо найти множества значений функции на каждом промежутке и взять их объединение.
Пример 7. Найдите области значений f(x) и f(f(x)), где
Найдём сначала множество значений функции f(x) на луче (-∞;1], где она совпадает с выражением 4 x + 9·4 -x + 3. Обозначим t = 4 x . Тогда f(x) = t + 9/t + 3, где 0 2 . На промежутке (0;4] производная g’(t) определена и обращается там в нуль при t = 3. При 0 1 функция f(x) совпадает с выражением 2cos(x-1) 1/2 + 7. Квадратный корень (x-1) 1/2 при x > 1 определён и принимает все положительные значения, поэтому cos(x-1) 1/2 принимает все значения от -1 до 1 включительно, а выражение 2cos(x-1) 1/2 + 7 принимает все значения от 5 до 9 включительно. Следовательно, множеством значений функции f(x) на луче (1;+∞) будет отрезок [5;9].
Теперь, объединив промежутки [9;+∞) и [5;9] – множества значений функции f(f(x)), обозначим t = f(x). Тогда f(f(x)) = f(t), где 
Аналогично, обозначив z = f(f(x)), можно найти область значений E(f 3 ) функции f(f(f(x))) = f(z), где 5 ≤ z ≤ 9 и т.д. Убедитесь, что E(f 3 ) = [2cos8 1/2 + 7; 2cos2 + 7].
Наиболее универсальным методом нахождения множества значений функции является использование наибольшего и наименьшего значений функции на заданном промежутке.
Пример 8. При каких значениях параметра р неравенcтво 8 x —р ≠ 2 x+1 – 2 x выполняется для всех -1 ≤ x x , запишем неравенство в виде р ≠ t 3 – 2t 2 + t. Так как t = 2 x – непрерывная возрастающая функция на R, то при -1 ≤ x -1 ≤ t 2 ↔
0,5 ≤ t 3 – 2t 2 + t при 0,5 ≤ t 2 – 4t + 1. Следовательно, f(t) дифференцируема, значит, и непрерывна на отрезке [0,5;4]. Из уравнения f’(t) = 0 найдём критические точки функции t = 1/3, t = 1, первая из которых не принадлежит отрезку [0,5;4], а вторая принадлежит ему. Так как f(0,5) = 1/8, f(1) = 0, f(4) = 36, то, по свойству дифференцируемой функции, 0 – наименьшее, а 36 – наибольшее значение функции f(t) на отрезке [0,5;4]. Тогда f(t), как непрерывная функция, принимает на отрезке [0,5;4] все значения от 0 до 36 включительно, причём значение 36 принимает только при t = 4, поэтому при 0,5 ≤ t
Данная тема имеет практическое значение. В школьном курсе математики изучается тема “Область значения функции”. Такие задачи обязательно содержатся в заданиях различных математических тестов, в частности в заданиях единого государственного экзамена.
Результаты работы можно использовать на уроках и дополнительных занятиях при подготовке учащихся выпускным и вступительным экзаменам, при самостоятельной подготовке учащихся по данной теме.
- Сильвестров В.В. Множество значений функции: Учебное пособие.– Чебоксары, 2004.
- Амелькин В.В., Рабцевич В.Л. Задачи с параметрами.– Минск, 1996.
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. – Москва – Харьков, 1998.
- Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами: Учебное пособие. 4-е изд., доп., перераб. – М., 2006.
- Сильвестров В.В. Неравенства с параметром на едином государственном экзамене // Математика для школьников. 2008. № 2.
http://zaochnik.com/spravochnik/matematika/funktsii/kak-najti-oblast-opredelenija-funktsii/
http://urok.1sept.ru/articles/592706

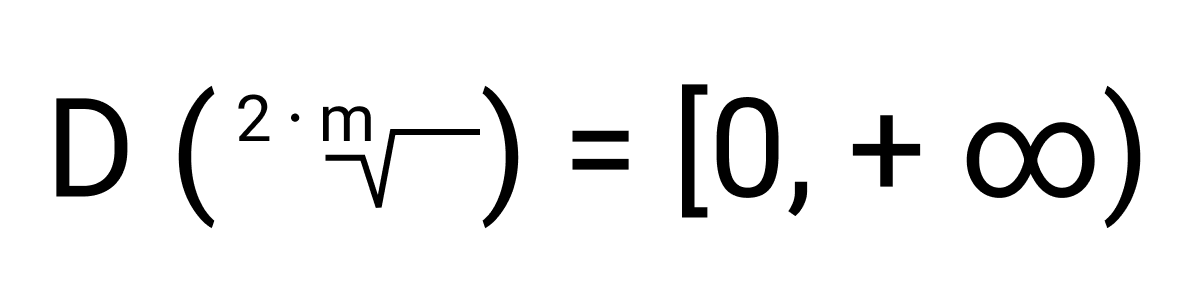
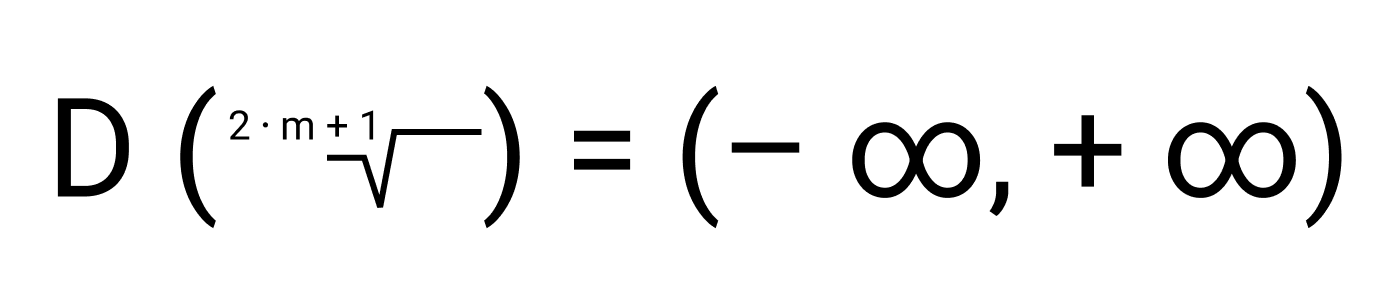


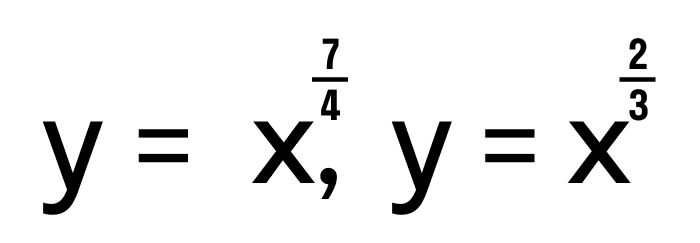 определены на интервале [0, +∞), так как их показатели положительные, но не целые.
определены на интервале [0, +∞), так как их показатели положительные, но не целые.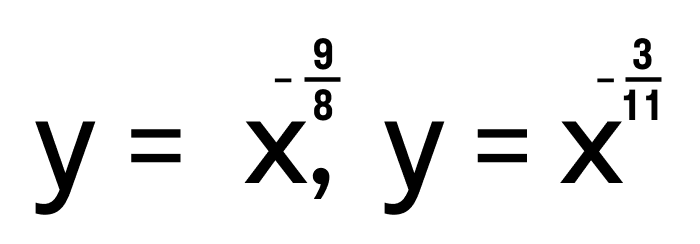 — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.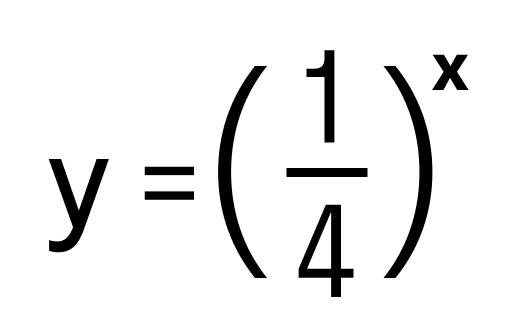
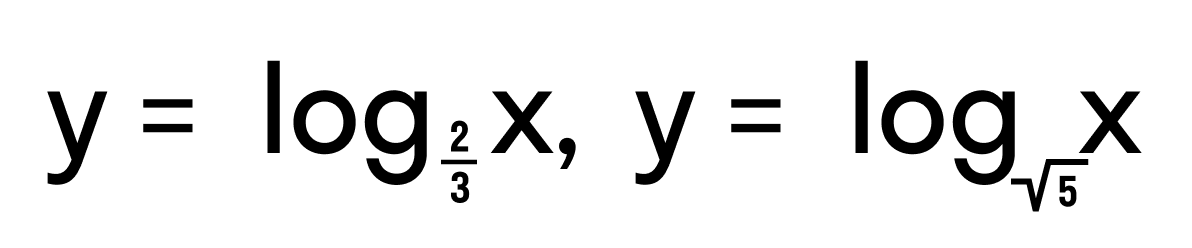



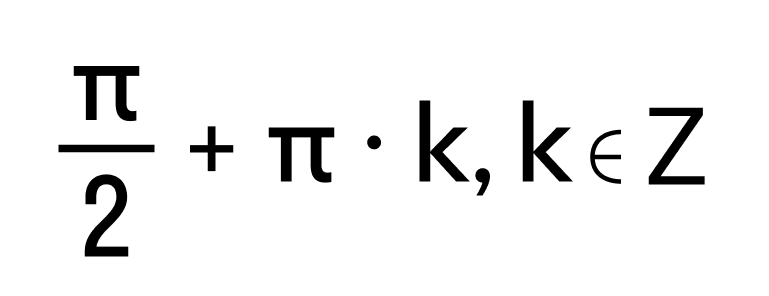 . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.








