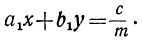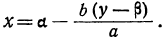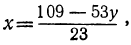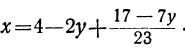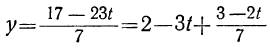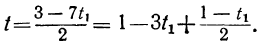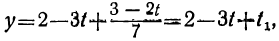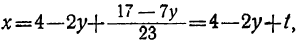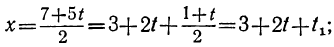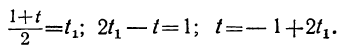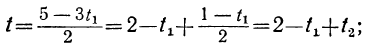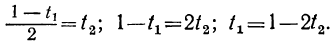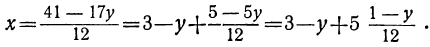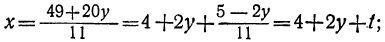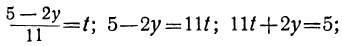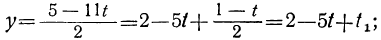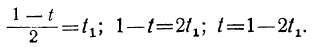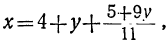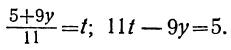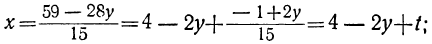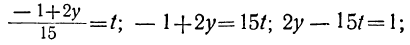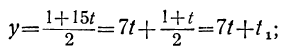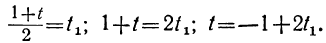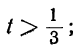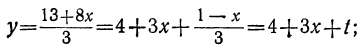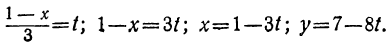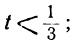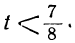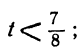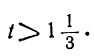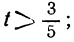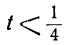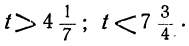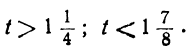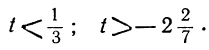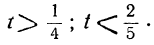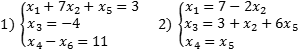Как определить определенное или неопределенное уравнение
линейных уравнений называется совместной, если у неё есть хотя бы одно решение, и несовместной, если решений нет. В примере 14 система совместна, столбик является её решением:
Это решение можно записать и без матриц: x = 2, у = 1.
Систему уравнений будем называть неопределённой, если она имеет более одного решения, и определённой, если решение единственно.
Пример 15. Система является неопределённой. Например, . являются её решениями. Читатель может найти и много других решений этой системы.
Научимся решать системы линейных уравнений сначала в частном случае. Систему уравнений AX = B будем называть крамеровской, если её основная матрица А — квадратная и невырожденная. Другими словами, в крамеровской системе число неизвестных совпадает с числом уравнений и |A| = 0.
Теорема 6 (правило Крамера). Крамеровская система линейных уравнений имеет единственное решение, задаваемое формулами:
где Δ = |A| — определитель основной матрицы, Δi — определитель, полученный из A заменой i-го столбика столбиком свободных членов.
Доказательство проведём для n = 3, так как в общем случае рассуждения аналогичны.
Итак, имеется крамеровская система:
Допустим сначала, что решение системы существует, т. е. имеются
Умножим первое . равенство на алгебраическое дополнение к элементу aii, второе равенство — на A2i, третье — на A3i и сложим полученные равенства:
Неопределенные уравнения в математике с примерами решения и образцами выполнения
При изучении уравнений первой степени мы уже видели, что если число уравнений меньше числа неизвестных, то такая система имеет бесчисленное множество решений. Такие уравнения называются неопределёнными.
Наиболее часто в практике встречается случай одного уравнения с двумя неизвестными. Общий вид такого уравнения будет:
αx+by=c,
где x и у—неизвестные, а, b и с—данные коэффициенты.
Часто условия задачи бывают таковы, что правильный ответ на вопрос, поставленный в задаче, дают только целые значения, а иногда только целые и притом положительные значения.
Задача:
Разложить число 118 на такие два числа, из которых одно делилось бы на 11, а другое на 17.
Обозначая одно число через Их, а другое через 17у, мы получим уравнение:
11x+17y=118.
Так как в задаче ничего не сказано о знаке чисел, на которые нужно разложить число 118, то в данном случае мы можем считать ответом на задачу и отрицательные решения. Так, условию задачи удовлетворяют числа 33 и 85 (при х=3 и у=5), но также удовлетворяют и числа 220 и —102 (при х=20 и у=—6).
Задача:
Для упаковки самоваров имеются ящики, из которых в одни укладываются 4 самовара, в другие 7. Сколько нужно взять тех или других ящиков, чтобы упаковать 41 самовар?
Обозначив число малых ящиков через х, а число больших через у, будем иметь уравнение:
4x-+7y=41.
Очевидно, что по условию задачи здесь пригодны только целые и притом положительные решения. Такое решение данное уравнение допускает лишь одно, именно: x=5, у=3.
Таким образом, необходимо уметь решать неопределённые уравнения в целых числах, а также в целых и положительных числах.
Признак невозможности решения уравнения в целых числах
Если среди коэффициентов а, b и с имеются дробные, то мы можем привести все коэффициенты к одному знаменателю и затем его отбросить. Тогда все коэффициенты будут целыми числами.
Далее, если а, b и с имеют какой-либо общий множитель, то на него можно сократить обе части уравнения.
Итак, мы будем предполагать, что коэффициенты a, b и с —числа целые, не имеющие общего множителя.
Предположим теперь, что а и b имеют общим множителем некоторое целое число, отличное от 1. Пусть, например,
a=ma₁, b=mb₁.
Разделив все его члены на m, получим:
При целых значениях х и у левая часть уравнения представляет собой целое число, правая же часть — дробь, так как с, по предположению, не делится на m. Такое равенство невозможно. Следовательно:
Если коэффициенты при неизвестных неопределённого уравнения имеют общий множитель, которого не имеет свободный член, то уравнение не может иметь целых решений.
Поэтому во всех дальнейших рассуждениях мы будем предполагать числа а и b взаимно простыми.
Признак невозможности решения уравнения в положительных числах
Пусть в уравнении ax+by=c коэффициенты а и b положительны, а свободный член с — отрицателен. Тогда при всяких положительных значениях х и у левая часть уравнения будет положительной, а правая останется отрицательной. Такое равенство невозможно.
Если коэффициенты а и b отрицательны, а с — положительно, то, умножив все члены уравнения на —1, мы сведём этот случай к предыдущему. Итак:
Если коэффициенты при неизвестных неопределённого уравнения имеют знаки, противоположные знаку свободного члена, то уравнение не имеет положительных решений.
Общая формула корней неопределённого уравнения
Предположим, что каким-либо способом (например, путём непосредственных проб) мы нашли одно целочисленное решение неопределённого уравнения:
ax+by=с.
Пусть это решение будет х=а и y=β. Подставляя значение x и у в данное уравнение, получим тождество:
a a+bβ =c.
Вычитая почленно это тождество из данного уравнения, получим:
α(x-α)+b(y-β)=0,
откуда:
ax=aa — b(y—β), или
Для того чтобы x было целым числом, необходимо и достаточно, чтобы выражение было целым числом (так как а—число
целое). Другими словами, необходимо и достаточно, чтобы выражение b(y-β) нацело делилось на а. Но, по предположению, b — число взаимно простое с а, следовательно, необходимо (и достаточно), чтобы разность у—β нацело делилась на а. Обозначив целое частное от деления у— β на а через t (оно может быть и положительным и отрицательным), получим:
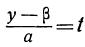
Подставляя в формулу для х число t вместо дроби 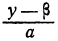
x = a-bt.
Таким образом, мы имеем для корней неопределённого уравнения формулы:
x = a-bt, y=β+at.
Давая в этих формулах t произвольные целые значения, положительные и отрицательные, мы получим бесчисленное множество целых решений данного неопределённого уравнения. В частности, при t=0 получим решение х = а; y=β, найденное нами уже ранее.
Присматриваясь к найденным формулам, легко заметить, что они составлены по следующему правилу:
- Первым членом формулы является найденное частное значение данного неизвестного.
- Вторым членом формул является произвольное целое число t, умноженное на коэффициент данного уравнения, причём в формуле для x берётся коэффициент при у в данном уравнении, а в формуле для у берётся коэффициент при х.
- Один из коэффициентов берётся с обратным знаком.
Нетрудно видеть, что совершенно безразлично, который из коэффициентов мы берём с тем же знаком, с каким он стоит в уравнении и который берём с обратным знаком. В самом деле, формулы:
x=a-bt, y=β+at и x=a+bt, y=β -at
будут давать одни и те же решения; только те решения, которые одни формулы дают при положительных значениях t, другие будут давать при равных по абсолютной величине отрицательных значениях t.
Пример:
Непосредственной подстановкой убеждаемся, что уравнение удовлетворяется значениями х=2 и у=4. Тогда все остальные решения найдутся из формул:
x=2+5t, у=4—3t, или х=2—5t, y=4+3t.
Давая в этих формулах t произвольные целые значения, будем получать различные целочисленные решения данного уравнения. Например, взяв первые формулы, будем иметь:
| t | 0 | 1 | 2 | 3 | -1 | -2 | … |
| x | 2 | 7 | 12 | 17 | -3 | -8 | … |
| y | 4 | 1 | -2 | -5 | 7 | 10 | … |
Если бы мы взяли вторые формулы, то те же решения получили бы, давая t последовательно значения: 0; —1; —2; —3; 1; 2 и т. д.
Таким образом, задача решения в целых числах неопределенного уравнения сводится к нахождению какого-либо одного решения.
Способ подстановки
Для нахождения одного решения неопределённого уравнения можно пользоваться следующим способом. Пусть дано уравнение:
ах+by=с.
Определим из него одно из неизвестных в зависимости от другого (лучше взять то, у которого коэффициент меньше). Пусть, например, a Частный вид неопределённого уравнения
Неопределённое уравнение легко решается в общем виде, когда один из коэффициентов при неизвестных равен единице. Пусть, например, равен единице коэффициент при х. Будем иметь:
x+by=c.
Определим х:
x=c-by.
Очевидно, что любому целому значению у будет соответствовать целое же значение х.
Пример:
Дано уравнение: 5x+y=18.
Находим:
у = 18—5х.
Давая x произвольные целые значения, будем соответственно получать целые значения для у:
| x | 0 | 1 | 2 | 3 | 4 | -1 | -2 | … |
| y | 18 | 13 | 8 | 3 | -2 | 23 | 28 | … |
Общее решение неопределённого уравнения
Покажем на примере способ решения неопределённого уравнения с любыми коэффициентами. Пусть дано уравнение:
23x+53y=109.
Определим из этого уравнения то неизвестное, у которого коэффициент меньше, в данном случае х:
или, исключив целую часть:
Для того чтобы x было целым при у целом, необходимо и достаточно, чтобы выражение 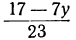
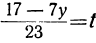
Если мы найдём для у и t такие целые значения, которые удовлетворяют уравнению 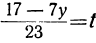
23t+7y=17,
то тем самым мы найдём соответствующие целые значения для х, и наша задача будет решена. Таким образом, решение данного уравнения мы свели к решению другого, более простого уравнения, у которого коэффициенты меньше, чем у данного.
По отношению к новому уравнению поступаем таким же образом. Определяем из него у:
Для того чтобы у было целым, необходимо и достаточно, чтобы 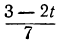
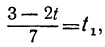
При целых t и t₁, удовлетворяющих последнему уравнению, мы получим соответственно целые значения для х и у, удовлетворяющие данному уравнению. Следовательно, наша задача свелась к решению последнего уравнения, у которого коэффициенты ещё меньше. Поступаем с ним так же, как и прежде:
Приравняв выражение 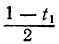
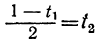
Мы получили уравнение, в котором коэффициент при одном из неизвестных равен единице, а такие уравнения решать мы уже умеем. Решив его, получим:
t₁=1-2t₂.
Давая в этом уравнении произвольные целые значения t₂, будем получать целые значения для t₁. Подставляя найденные целые значения t₁ и t₂ в выражение для t: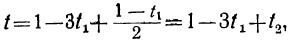
получим соответствующие целые значения для t. Подставляя соответствующие пары значений t и t₁ в выражение для у:
получим соответствующие целые значения для у. Наконец, делая подстановку найденных значений для у и t в выражение для х:
получим соответствующие целые значения для х.
Можно, однако, прямо выразить х и у в зависимости от t₂. Для этого подставим в выражение для t вместо t₁ его выражение через t₂:
t=1-3t₂+t₂=1-3 (1—2t₂)+t₂ ,
или
t=-2+7t₂ .
Подставим теперь в выражение для у вместо t и t₁ их выражения через t₂:
y=2-3t+t₁=2-3(-2+7t₂) + (1- 2t₂),
или
y=9-23t₂.
Наконец, подставляя найденные значения у и t в выражение для х, получим:
x=4-2y+t=4-2(9-23t₂)+(-2+7t₂),
или
x=- 16+53t₂ .
Таким образом, мы получим для х и у формулы:
x= — 16+53t₂, y=9-23t₂.
Давая в них произвольные целые значения для t₂, как положительные, так и отрицательные, будем получать бесчисленное множество решений данного уравнения; некоторые из них помещены в следующей таблице:
| t₂ | 0 | 1 | 2 | -1 | -2 |
| x | -16 | 37 | 90 | -69 | -122 |
| y | 9 | -14 | -37 | 32 | 55 |
Рассматривая операции, которые производились над коэффициентами данного и следующих уравнений, можно заметить такую последовательность:
- Больший коэффициент данного уравнения 53 делили на меньший 23; получили частное 2 и остаток 7.
- Меньший коэффициент данного уравнения 23 делили на остаток 7; получили частное 3 и второй остаток 2.
- Первый остаток 7 делили на второй остаток 2; получили частное 3 и третий остаток 1.
Другими словами, мы поступали точно так, как если бы находили общий наибольший делитель коэффициентов данного уравнения.
Мы знаем, что два взаимно простых числа имеют общим наибольшим делителем единицу. А так как в неопределённом уравнении мы всегда предполагаем коэффициенты при неизвестных взаимно простыми, то производя над уравнением указанные выше операции, мы всегда придём к такому уравнению, у которого коэффициент при одном из неизвестных равен единице. Тем самым мы находим решения и данного уравнения. Отсюда следует:
Если коэффициенты при неизвестных неопределённого уравнения-числа взаимно простые, то уравнение всегда имеет целые решения.
Упрощение решения уравнения. Иногда при решении неопределённого уравнения можно внести некоторые упрощения, позволяющие быстрее прийти к решению.
1. В случае, когда один из коэффициентов при неизвестных и свободный член имеют общий множитель, то на него можно сократить обе части уравнения, если надлежащим образом ввести новое неизвестное.
Пример:
Коэффициент 6 и свободный член имеют общим множителем 3. Следовательно, и член 5у должен делиться на 3, а так как 5 не делится на 3, то у должен быть кратным трём. Полагая у=3t, где t— целое число, будем иметь:
6x-15t=21,
или, по сокращении на 3:
2x-5t =7.
Решаем последнее уравнение:
Подставляя найденное значение в выражения, полученные для х и у, будем иметь:
x=3+2(-1+2t₁)+t₁ =1+5t₁;
y=3(-1+2t₁) = -3+6t₁ .
Пример:
Дано уравнение: 9x+14y=105.
Полагая у=3t и сокращая обе части уравнения на 3, получим:
3x+14t=35.
Полагая в этом уравнении x=7t₁ и сокращая обе части уравнения на 7, получим:
3t₁ +2t=5.
Решаем последнее уравнение:
Произведя последовательные подстановки, получим:
t=2-(1-2t₂) + t₂ = 1+3t₂;
x=7t₁=7(1-2t₂)=7-14t₂ ;
y=3t=3(1+3t₂) = 3+9t₂ .
2. Если в приравниваемом целому числу выражении члены, находящиеся в числителе, имеют общий множитель, то решение уравнения можно упростить.
Пример:
Дано уравнение: 12x+17y=41.
Решаем его относительно х:
Для того чтобы выражение 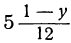
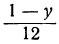
Приравнивая это выражение целому числу t, получим: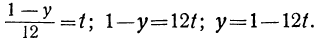
Соответственно получаем для х:
x=3-(1-12t)+5t=2+17t
3. Если при выделении целой части остаток будет более половины делителя, то удобно ввести отрицательный остаток.
Пример:
Дано уравнение: 11х—20y=49.
Решим его относительно х:
Произведя подстановки, получим:
y=2-5(1-2t₁)+t₁ = -3+11t₁;
x=4+2(-3+ 11t₁)+(1-2t₁) = -1+20t₁.
Если бы решали данное уравнение обычным способом, то получили бы для х:
и следующее уравнение было бы:
Это уравнение сложнее уравнения, полученного нами при помощи введения отрицательного остатка:
11t+2y=5.
Пример:
Дано уравнение: 15x+28y=59.
Решаем уравнение относительно х, вводя отрицательные остатки:
Попробовав решить приведённые в примерах уравнения обычным путём, легко убедимся, что без применения указанных упрощений все они потребовали бы для решения большего числа операций.
Положительные решения
Как уже говорилось ранее, часто из всех найденных решений неопределённого уравнения нужно взять лишь те, которые дают одновременно положительные значения для х и у. Найдя общие формулы для х и у, можно сразу определить, при каких значениях произвольного множителя будут получаться целые и положительные значения х и у.
Для того чтобы x и у были положительными, необходимо брать для t только такие значения, при которых:
a+bt>0; β-αt>0.
Будем считать а числом положительным. (Это мы всегда имеем право предположить, так как в противном случае мы могли бы обе части уравнения умножить на —1.) Тогда могут встретиться три различных случая.
1. Оба неравенства одинакового смысла. Это случится когда b — число отрицательное. В самом деле, пользуясь свойствами неравенства, будем иметь:
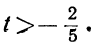
bt > — a ; at 0; 2+-5t>0,
или
Взяв для t любое целое число, большее 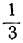
Пример:
Решаем уравнение:
Ищем положительные решения:
1 —3t>0; 7 —8t>0,
или
Любое целое значение t, меньшее 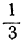
2. Неравенства противоположного смысла, причём они противоречат одно другому. Пусть, например, мы получим следующие неравенства:
Очевидно, что не существует таких значений t, которые одновременно удовлетворяли бы обоим неравенствам. В этом случае уравнение не может иметь положительных решений.
Пример:
4x+5y=-7.
Решая это уравнение, получим:
х=— 3+5t; y=1—4t.
Отсюда:
— 3+5t>0; 1 — 4t>0,
или
Неравенства противоречат друг другу; уравнение не имеет положительных решений.
3. Неравенства противоположного смысла, причём они не противоречат друг другу. Пусть, например, мы получили неравенства:
Все целые значения t, заключающиеся между 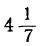
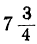
6 и 7, дадут для х и у положительные решения. Таким образом, в этом случае:
Уравнение имеет столько целых положительных решений, сколько целых чисел заключено между найденными пределами для t.
Заметим, что, в частности, уравнение и здесь может не иметь положительных решений. Это будет тогда, когда между найденными пределами для t не содержится ни одного целого числа. Например, пусть мы получим неравенства:
Неравенства не противоречат друг другу, но между 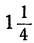
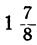
находится ни одного целого числа. Уравнение не имеет целых положительных решений.
Пример:
3x+7y=55.
Решаем уравнение: 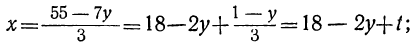
у=1 — 3t; x= 16+7t.
Отсюда:
1 —3t>0; 16+7t> 0,
или
Очевидно, для / можно взять лишь значения: 0; —1; —2. Получаем три решения уравнения:
| t | 0 | -1 | -2 |
| x | 16 | 9 | 2 |
| y | 1 | 4 | 7 |
Пример:
5. 5x+4y=3.
Решая уравнение, получим:
х=— 1 + 4t; у=2 —5t.
Отсюда:
Неравенства не противоречат друг другу; но между 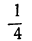
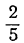
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Системы линейных уравнений: основные понятия
— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
— это последовательность чисел ( k 1, k 2, . kn ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1, x 2, . xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Переменная xi называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
Обе системы являются разрешенными относительно переменных x 1, x 3 и x 4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x 1, x 3 и x 5. Достаточно переписать самое последнее уравнение в виде x 5 = x 4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1, x 2 = b 2, . xk = bk ;
- Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x 2, x 5, x 6 (для первой системы) и x 2, x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.
Теорема. Если в системе из n уравнений переменные x 1, x 2, . xr — разрешенные, а x r + 1, x r + 2, . x k — свободные, то:
- Если задать значения свободным переменным ( x r + 1 = t r + 1, x r + 2 = t r + 2, . xk = tk ), а затем найти значения x 1, x 2, . xr , получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
http://lfirmal.com/neopredelennye-uravneniya/
http://www.berdov.com/works/algebra/system_of_linear_equations/