Как определить по коэффициентам тип уравнения

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.

Напомним, что y ‘ = d x d y , если y является функцией аргумента x .

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3

Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .

Приведем примеры подобных дифференциальных уравнений:

e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1

Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .

Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )

Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x

Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.

В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .

К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .

Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .

Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.

Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .

Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .

Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0

Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .

Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:

y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x

Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2

Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0

Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.

Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R

Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :

• действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
• комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

• y = C 1 e k 1 x + C 2 e k 2 x ;
• y = C 1 e k x + C 2 x e k x ;
• y = e a · x · ( C 1 cos β x + C 2 sin β x ) .

Пример 13

Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:

y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2

Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R

Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.

К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:

y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .

Частные решения мы можем выбрать из систем независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.

В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .

Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.

В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

• находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
• записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

— частное решение неоднородного дифференциального уравнения.

y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Как определить a, b и c по графику параболы

Предположим, вам попался график функции \(y=ax^2+bx+c\) и нужно по этому графику определить коэффициенты \(a\), \(b\) и \(c\). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью \(y\) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент \(a\) можно найти с помощью следующих фактов:

— Если \(a>0\), то ветви параболы направленных вверх, если \(a 1\), то график вытянут вверх в \(a\) раз по сравнению с «базовым» графиком (у которого \(a=1\)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: \(y=ax^2+bx+c\). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим \(9a\) вместо \(b\):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки \(A\) и \(B\) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение \(a\):

Получается квадратичная функция: \(y=-x^2-9x-15\).

Сразу заметим, что по графику можно сразу определить, что \(c=4\). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: \(C(-1;8)\), \(D(1;2)\) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).

– Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.

– График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
— График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц.

График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).

То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:

Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).

Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).

Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).

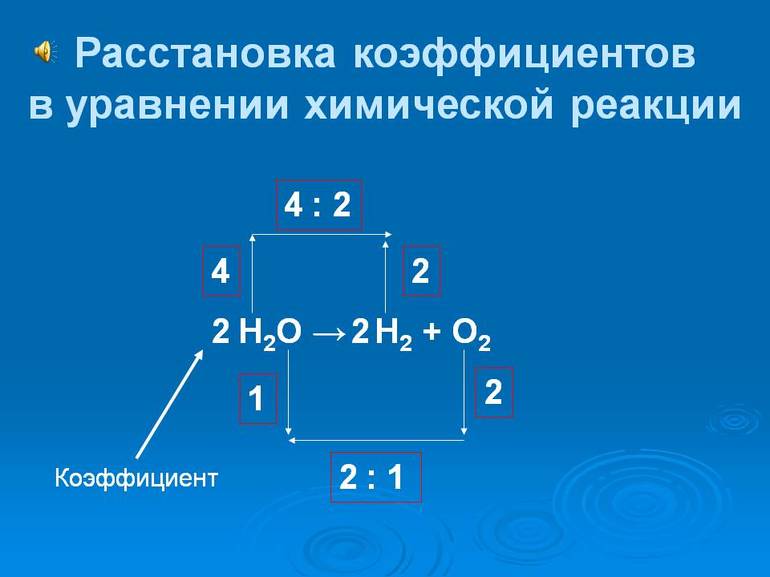
Коэффициенты в химических уравнениях — как правильно расставлять и уравнивать

Краткое описание

Всем достоверно известно, что диоксид углерода (СО2) и вода (Н2О) образуются в результате горения метана (СН4) в кислороде (О2). Это химическое явление элементарное и вполне логическое. Саму реакцию можно обозначить следующим уравнением: СН4+О2→СО2+Н2О. Если ученик решил более углублённо заняться изучением этой удивительной науки, то наверняка ему будет интересно постараться извлечь из этого примера химического уравнения гораздо больше ценной информации, нежели просто просмотреть запись всех реагентов, а также продуктов реакции.

Уравнение относится к категории неполных, из-за чего неподготовленный ученик не может быстро посчитать, сколько именно молекул О2 уходит на одну молекулу метана, а также какое количество молекул диоксид углерода и воды можно получить в сумме. В такой ситуации может помочь дополнительная запись данных перед соответствующими молекулярными формулами (численные стехиометрические коэффициенты).

Указанные цифры будут обозначать, сколько именно молекул каждого вида будет принимать активное участие в химической реакции. В химии часто используется стехиометрия (направление науки, которое занимается изучением количественного соотношения между веществами, вступившими в реакцию и сформированными во время этого процесса продуктами) для переноса зарядов.

Чтобы ученик мог логическим образом закончить составление уравнения, необходимо усвоить одно, но очень важное правило: в обеих частях примера должно присутствовать равное число атомов каждой разновидности. Во время химических реакций не образуются новые атомы, а также не происходит ликвидация имеющихся молекул. Именно это правило базируется на законе сохранения массы, что тоже нужно запомнить.

Востребованные сегодня онлайн-калькуляторы позволяют найти ответы на самые сложные задания, а также выстроить поэтапно алгоритм решения более сложных упражнений.

Правильная запись реакций

Различные примеры того, как можно уравнивать химические реакции позволяют ученикам лучше усвоить то, каким именно образом принято расставлять коэффициенты в уравнениях. Для избежания грубых ошибок нужно подробно разобраться во всех нюансах. Если ученику необходимо записать правильное уравнение, которое сможет подтвердить базовые характеристики метана, тогда ему следует выбрать один из следующих вариантов:

1. Элементарное горение в воздухе кислорода.
2. Специфическое галогенирование (специфическое взаимодействие с элементом типа VIIA).

Стоит отметить, что для первого варианта в левой части пишут первоначальное вещество, а вот в правой подробно описаны полученные во время реакции продукты. После тщательной проверки количества атомов можно сформировать оптимальную финальную запись происходящего процесса. Во время произведённых экспериментов специалистами было доказано, что в результате горения метана в кислороде неизбежно происходит своеобразный экзотермический процесс. В итоге возникает углекислый газ и водяной пар.

Чтобы уметь правильно расставлять коэффициенты в химических уравнениях, необходимо прибегнуть к действующему закону сохранения массы веществ.

Лучше всего начинать процесс уравнения с определения точного количества атомов углерода. На финальном этапе остаётся только выполнить все необходимые расчёты для водорода, чтобы после этого иметь возможность проверить количество кислорода. Базовые значения задействованных элементов можно узнать из специальной таблицы.

Ключевые нюансы

Для правильного решения поставленных задач ученики обязательно должны знать, что собой представляет балансировка химических уравнений. Элементарное уравнение необходимо для того, чтобы из самого обычного примера получить максимально развёрнутый результат.

Проще всего начинать изучение этой темы с углерода. В левой части присутствует всего один атом С, который является неотъемлемым компонентом состава молекулы СН4. А вот с правой стороны содержится одна молекула С, которая дополняет состав СО2. Это значит, что в двух присутствующих частях итоговое количество атомов углерода максимально совпадает, из-за чего нет необходимости выполнять какие-либо действия. Просто для лучшего понимания всех нюансов можно поставить единицу в качестве коэффициента перед молекулами с углеродом. Итоговая формула примет следующий вид: 1СН4+О2→1СО2+Н2О.

После всех проделанных манипуляций можно подсчитать количество атомов водорода. С левой стороны присутствует четыре атома H в составе СН4, а вот с правой — только два атома, которые входят в состав Н2О. После этого остаётся только всё уровнять. Для этих целей достаточно записать коэффициент 2 перед молекулой Н2О. В итоге не только в реагентах, но и в полученных продуктах будет по четыре молекулы водорода. Формула будет выглядеть так: 1СН4+О2→1СО2+2Н2О.

Во время расстановки коэффициентов методом электронного баланса очень важно не только разбираться в химии, но и владеть элементарными математическими навыками. Если изучить этот пример — 1СН4+2О2→1СО2+2Н2О, то можно понять, как выглядит полноценное уравнение исследуемой химической реакции. В этом случае полностью соблюдается закон о сохранении имеющейся массы.

Число атомов, которые вступают в сложную реакцию, максимально совпадает с итоговым количеством веществ определённого сорта по окончании реакции. Но ученику нужно хорошо понимать тот факт, что возникающая реакция представляет собой весьма специфическую последовательность отдельных промежуточных стадий. Но даже успешное уравнение не может раскрыть всю информацию об изучаемом молекулярном механизме.

Понятие ОВР в химии

В учебной литературе подробно описано то, что даже самые сложные уравнения можно уровнять. Но для этих целей понадобятся знания в сфере того, как управлять методом электронного баланса либо полуреакций. Существует определённая последовательность всех манипуляций, которая была разработана специалистами для поэтапной расстановки всех коэффициентов в реакциях двух категорий:

1. Элементарное разложение.
2. Специальное замещение.

Для избежания грубых ошибок на первом этапе правильно расставляют степени окисления возле каждого задействованного элемента. В этом случае нужно учитывать ряд рекомендаций:

• Показатель окисления всегда равен нулю у простых компонентов.
• Если в состав соединения входит три и более элемента, тогда у первого вещества проявляется положительная характеристика, а вот у крайнего только отрицательное. Необходимый центральный элемент высчитывают исключительно при помощи математических знаний, но в итоге должен получиться ноль.
• В соединении бинарного типа степень окисления соответствует нулю.

После проделанных манипуляций учащемуся нужно выбрать те ионы либо атомы, показатель степени окисления которых можно преобразовать. Количеством электронов можно показывать при помощи знаков + и -. А также нельзя забывать о необходимости определить наименьшее кратное. Во время деления НОК можно находить максимально достоверный результат.

Определение коэффициентов

Лучше всего разобраться во всех нюансах на конкретном примере. Специалисты рекомендуют рассмотреть тринитротолуол (ТНТ) С7Н5 N 3О6. Этот элемент отлично соединяется с кислородом, благодаря чему образуется Н2О, СО2, а также N2. Чтобы не запутаться, данные могут записаться в виде обычного уравнения реакций, с которым нужно будет активно работать: C7H5N3O6+O2→CO2+H2O+N2.

Гораздо проще самостоятельно составлять максимально развёрнутую химическую задачу, базируясь во время этого на двух молекулах тринитротолуола, так как с левой стороны содержится нечётное количество атомов азота и водорода, а с правой записывают чётное число молекул. Если изучить приведённый пример, то становится понятно, что атомы углерода, водорода и азота содержатся в соотношении 14:10:6. Но после нехитрых действий они подвергнутся изменениям. В итоге можно будет получить молекулы воды, диоксид углерода и азота (соотношение 5:14:3).

Полное химическое уравнение примет следующий вид — 4C7H5N3O6 + 21O2 → 28CO2 + 10H2O + 6N2. Пример несёт в себе много полезной информации, которая первым делом указывает на исходные вещества — конкретные реагенты, а также другие химические продукты. Во время реакции индивидуально сохраняются абсолютно все атомы каждого сорта.

Если попробовать умножить обе части уравнения на число Авогадро (NA=6,022·10 23 ), то в итоге можно будет смело утверждать, что 4 моля ТНТ реагируют на 21 моль О2. После такого «контакта» могут сформироваться 28 молей СО2, 10 молей Н2О, а также 6 молей N2.

Решение классической задачи

Если учащемуся необходимо определить точный объём раствора хлороводорода 10%, стандартная плотность которого находится в пределах 1,05 г/мл, тогда нужно знать, что эта жидкость идеально подходит для полной ликвидации гидроксида кальция, неизбежно формирующегося в процессе гидролиза его карбида. Из химии всем хорошо известно, что во время этой процедуры в воздух выделяется специфический газ, объём которого составляет 8,96 л. Чтобы решить поставленную задачу без единой ошибки, нужно первым делом постараться составить уравнение для гидролиза карбида кальция.

Эта задача не является сложной, но только в том случае, если ученик хорошо усвоит все основные правила. Гидроксид кальция вступает во взаимодействие с хлороводородом, из-за чего происходит полноценная нейтрализация. На финальном этапе формула примет такой вид: Са (ОН)2+2HCI = CaCl2+2H2O. Обязательно нужно записать точную массу кислоты, так как она неизбежно понадобится для дальнейших действий. Остаётся установить объём задействованного раствора хлороводорода.

Абсолютно все расчёты по этой задаче должны выполняться в соответствии с коэффициентами стереохимического типа, что лишний раз подтверждает их актуальность.

Дополнительная информация

Если учитывать то, что в большинстве случаев расстановка коэффициентов вызывает определённые затруднения, тогда нужно отработать схему действий на конкретных примерах. Для лучшего понимания всех нюансов следует рассмотреть уравнение, которое связано с расстановкой важных данных в классической реакции окислительно-восстановительного типа. Нужно разобраться со следующей формулой: Н2S+HMnO4=S+MnO2…

Ключевая особенность этой задачи в том, что ученику нужно максимально дополнить утерянный продукт реакции, чтобы в итоге иметь возможность перейти к указанию всех необходимых коэффициентов. После правильной расстановки на положенные места базовых степеней окисления у каждого вещества в соединениях можно выполнить логический вывод, что первоначальные свойства проявляет только марганец, который понижает валентность. Восстановительную способность в этой реакции лучшим образом демонстрирует сера, которая восстанавливается до простого вещества.

После окончательного составления электронного баланса остаётся правильно расставить коэффициенты в предполагаемую схему химического процесса. На этом задачу можно считать выполненной.

Необходимо дополнительно поработать над нахождением наименьшего общего кратного, чтобы правильно делить, а также умножать числа. Расстановке коэффициентов в уравнениях обязательно нужно уделять должное внимание, так как это одна из основных тем в многогранной и интересной химии.