Как определить порядок фильтра по разностному уравнению

Как определить порядок фильтра по разностному уравнению

21.6. ЦИФРОВЫЕ ФИЛЬТРЫ, ИХ РАЗНОСТНЫЕ УРАВНЕНИЯ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ИМПУЛЬСНЫЕ ХАРАКТЕРИСТИКИ

Цифровой фильтр описывается тремя характеристиками — разностным уравнением , которому может быть поставлена в соответствие передаточная функция K ( z ) или полученная в результате обратного z -преобразования K ( z ) его дискретная импульсная характеристика h [ k ] . Из приведенных примеров следует, что существуют два принципиально различных класса цифровых фильтров. Фильтры первого класса — нерекурсивные — описываются разностным уравнением, в котором выходная величина y [ k ] выражается только через конечное число значений входного сигнала x [ n ] . Таким, например, является уравнение усреднения, рассмотренное выше.

Фильтры второго класса — рекурсивные — описываются уравнением, в котором выходная переменная y [ k ] выражается не только через значения входного сигнала x [ n ], но и через предшествующие значения выходного сигнала y [ k – m ] . Сюда, например, относится разностное уравнение u₂[ k + 1] = u₂[ k ] e -T/ t + u₁[ k ][h(T) – h(T – T_и)], описывающее преобразование прямоугольных сигналов RС -цепью (см. п. 20.4), а также дискретные модели любых других аналоговых динамических систем (в частности, электрических цепей).

Нерекурсивный цифровой фильтр сохраняет информацию о входном сигнале за конечное число шагов — его импульсная характеристика конечна, а передаточная функция имеет вид ряда по степеням z (который включает и отрицательные показатели).

Информация, поступившая на вход рекурсивного фильтра, сохраняется в нем бесконечно долго; он имеет бесконечную по длительности импульсную характеристику и описывается передаточной функцией в виде рациональной дроби. Максимальная разность индексов переменных в разностном уравнении, который отвечает разность степеней z в числителе и знаменателе передаточной функции, определяет порядок цифрового фильтра.

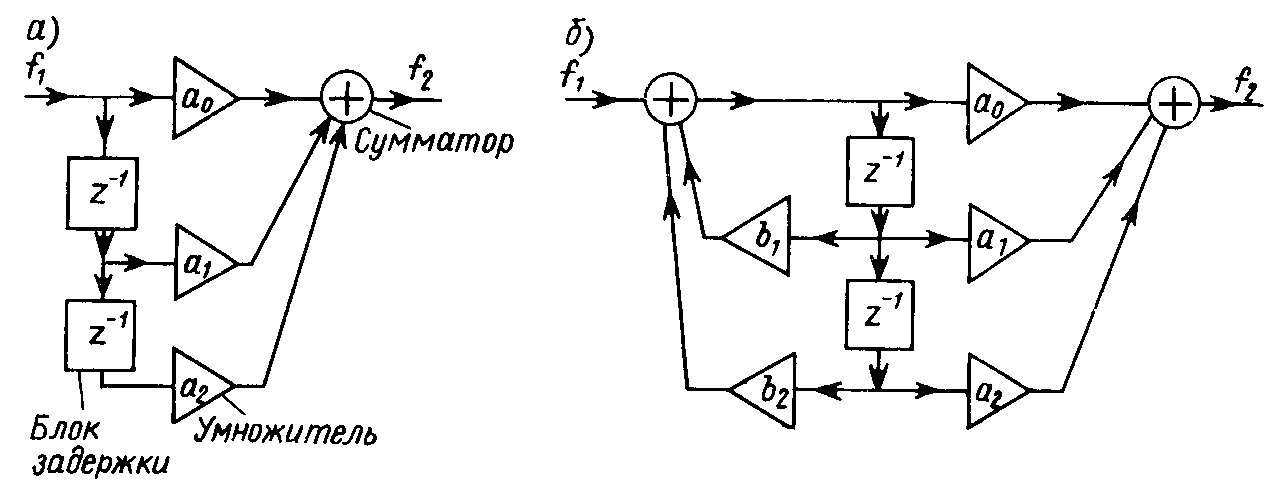
Так, нерекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2], его передаточная функция K ( z ) = a 0 + a 1 z –1 + a 2 z –2 , а импульсная характеристика определяется коэффициентами, h [ n ] = a 0 , a 1 , a 2 , 0, 0, 0, 0, .

Рекурсивный цифровой фильтр второго порядка описывается разностным уравнением f 2 [ n ] = a 0 f 1 [ n ] + a 1 f 1 [ n – 1] + a 2 f 1 [ n – 2] + b 1 f 2 [ n – 1] + b 2 f 2 [ n – 2],

а его передаточная функция — .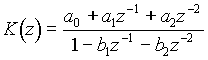

По известным значениям коэффициентов разностного уравнения a k и b k цифровой фильтр 2-го порядка может быть реализован с помощью умножителей, сумматоров и блоков задержки.

Блок-схемы цифровых фильтров обоих классов 2-го порядка, включающие перечисленные блоки, показаны на рис. 21.10 ( а – нерекурсивный; б – рекурсивный).

Преобразование Лапласа дискретного сигнала. Z-преобразование. Разностное уравнение дискретного фильтра

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

В предыдущих разделах мы подробно рассмотрели расчет аналоговых фильтров с заданными характеристиками. Пришло время переходить к анализу цифровых фильтров. Необходимо разделить понятия дискретного и цифрового фильтра.

Дискретным мы будем называть фильтр, импульсная характеристика которого является дискретной, а коэффициенты передаточной функции рассчитаны точно без ошибок округления.

Под цифровым фильтром мы будем понимать дискретный фильтр, коэффициенты передаточной характеристики которого рассчитаны не точно, а с ошибками округления вызванными конечной разрядностью представления числа.

На практике все рассчитанные фильтры являются цифровыми, так как разрядность представления числа ограничена. Однако использование компьютера позволяет производить операции с 64-битными числами с плавающей точкой, что минимизирует ошибки округления, поэтому можно предполагать, что рассчитанные с такой разрядностью фильтры «почти дискретные».

Важно отметить, что округление коэффициентов устойчивого дискретного фильтра, даже самое незначительное, может привести к неустойчивому цифровому фильтру. Поэтому при расчете фильтров, особенно фильтров высокого порядка, всегда необходимо проверять их устойчивость.

В цифровых системах сигналы представляют собой последовательности отсчетов, взятые, как правило, через равные промежутки времени . Ранее мы уже рассматривали модель дискретного сигнала :

Графически процесс дискретизации сигнала показан на рисунке 1.

Рассмотрим преобразование Лапласа дискретного сигнала :

Важное замечание. Если , то получаем дискретно-временное преобразование Фурье дискретного сигнала, при этом является периодической функцией частоты с периодом , кроме того, если , то

Кружочками условно показаны нули образа , а крестиками — полюсы.

Важно отметить, что периодичность дискретного преобразования Лапласа соответствует периодичности преобразования Фурье дискретного сигнала . Однако, как мы знаем из теории дискретного преобразования Фурье, на каждом периоде повторения спектр дискретного сигнала может быть искажен эффектом алиасинга, т.е. наложением «хвостов» исходной спектральной плотности из высших зон Найквиста (заполненная точками область на карте нулей и полюсов образа соответствует высшим зонам Найквиста).

В случае дискретного преобразования Лапласа эффект алиасинга сохраняется, и периодический образ на каждом периоде отличается от исходного образа . Так например, мы можем наблюдать алиасинг полюсов из высших зон Найквиста при неверном выборе частоты дискретизации. Если все полюсы исходного образа попадают в первую зону Найквиста, то при дискретизации они периодически разможатся, как это показано на рисунке 2.

Положение нулей дискретного преобразования Лапласа , как правило отличается от положения нулей исходного образа в результате эффекта алиасинга.

Рассмотрим процесс фильтрации дискретного сигнала . Согласно свойству преобразования Лапласа, процесс фильтрации во временно́й области сводится к умножению образа исходного сигнала на передаточную характеристику фильтра , которая в свою очередь, представляет преобразование Лапласа импульсной характеристики фильтра . Тогда преобразование Лапласа сигнала на выходе фильтра можно записать:

Первый случай. — образ дискретного сигнала, удовлетворяет (3), а — передаточная характеристика непрерывного фильтра, и свойство (3) не выполняется, значит также не удовлетворяето (3). Тогда можно сделать вывод о том, что при прохождении дискретного сигнала через аналоговый фильтр, выходной сигнал получается аналоговым. Аналоговый фильтр производит восстановление непрерывного сигнала по имеющемуся дискретному.

Второй случай. удовлетворяет (3), также удовлетворяет (3) (импульсная характеристика фильтра является дискретной), причем интервалы дискретизации сигнала и фильтра одинаковые и равны . Тогда в результате произведения также удовлетворяет (3). Таким образом, при прохождении дискретного сигнала через дискретный фильтр, выходной сигнал получается дискретным, с той же частотой дискретизации.

Третий случай. и удовлетворяют (3), но интервал дискретизации сигнала равен , а интервал дискретизации импульсной характеристики фильтра (исходный сигнал и и импульсная характеристика фильтра дискретизированы с разной частотой). В этом случае , в частных случаях, может удовлетворять (3), но период дискретизации выходного сигнала , будет равен «наименьшему общему кратному» периодов и . Заметим, что термин «наименьшее общее кратное» взят в кавычки, потому что и могут быть вещественными числами, в том числе и иррациональными. Тогда понимается как вещественное число, которое делится нацело как на , так и на . Например, если , а , то . Данный на практике не встречается, так как требует реализации цифровых схем, работающих на разных тактовых частотах. Разработка таких схем сопряжена с трудностями синхронизации при переходе данных из модулей, работающих на различных тактовых частотах.

Основное правило — для дискретных и цифровых фильтров интервалы дискретизации сигнала и фильтра должны быть равны.

Таким образом, для того чтобы на выходе фильтра получить дискретный сигнал, необходимо чтобы импульсная характеристика фильтра также была дискретной, а значит передаточная характеристика дискретного фильтра может быть представлена как результат дискретного преобразования Лапласа:

Если у дискретного фильтра количество коэффициентов ограничено, то такой фильтр называют фильтром с конечной импульсной характеристикой (КИХ-фильтром) [1] , а если количество коэффициентов бесконечно, то такой фильтр называют фильтром с бесконечной импульсной характеристикой (БИХ-фильтр) [2] .

При переходе от аналогового фильтра к цифровому, происходит периодическое размножение передаточной характеристики вдоль оси . При этом, переменная в образах дискретного преобразования Лапласа всегда присутствует только в показателе экспоненты, для обеспечения периодичности передаточных характеристик дискретных систем [1, стр 155].

В результате периодизации также происходит периодическое размножение нулей и полюсов, что доставляет некоторые неудобства. Для облегчения анализа вводят переменную вида:

Отображение не является конформным [2, стр. 145], потому что множество точек плоскости отображается в одну точку плоскости .

Графически отображение -плоскости в комплексную -плоскость показано на рисунке 3.

Рассмотрим некоторые особенности отображения (7).

Если , где , то для всех этих точек .

Если чисто вещественно, то и также вещественное, причем 0″/>. Заметим, что при , (внутри единичной окружности), а при величина (вне единичной окружности).

При , точка на мнимой оси плоскости отображается в точку , расположенную на единичной окружности и повернутой на угол рад. Таким образом, вся мнимая ось плоскости отображается в единичную окружность плоскости . Причем, один оборот единичной окружности соответствует от до рад/c.

Левая полуплоскость комплексной плоскости отображается внутрь единичной окружности плоскости . Действительно если , то представляет вектор длины повернутый на угол рад. При , длина вектора .

Правая полуплоскость комплексной плоскости отображается вне единичной окружности плоскости .

При переходе из комплексной -плоскости в комплексную -плоскость все бесконечно-повторяющиеся нули и полюса дискретного фильтра в -плоскости отображаются в конечное количество нулей и полюсов в -плоскости. Тогда выражение для передаточной характеристики дискретного фильтра может быть представлено при помощи подстановки (7) через конечное количество нулей и полюсов в -плоскости как:

Таким образом, главный вывод, который мы должны сделать заключается в следующем: при переходе от аналогового фильтра к дискретному, образ по Лапласу становится периодическим по мнимой оси, а количество нулей и полюсов фильтра бесконечным. Но при переходе в комплексную –плоскость мы получаем снова конечное количество нулей и полюсов, и соответственно конечное количество коэффициентов дискретного фильтра.

Рассмотрим некоторые свойства -преобразования. При этом мы будем рассматривать свойства относительно индексов отсчетов в предположении . В результате мы можем опустить период дискретизации в выражениях -преобразования.

Линейность. -образ суммы двух сигналов равен сумме -образов этих сигналов. Действительно, пусть есть два дискретных сигнала и , . Найдем -преобразование их суммы :

Можно показать, что данное свойство также справедливо и для циклической задержки ограниченной выборки сигнала:

Теорема о свертке. Пусть дано два сигнала ограниченной длительности и , . Найдем -преобразование их циклической свертки :

При выводе было использовано свойство циклической задержки -преобразования. Таким образом циклическая свертка сигналов соответствует произведению их -образов.

Аналогично, используя свойство задержки, можно показать, что -образ линейной свёртки сигналов равен произведению их -образов:

Ранее мы говорили о том, что пассивные аналоговые цепи описываются интегро-дифференциальными уравнениями непрерывного времени . При этом математический аппарат преобразования Лапласа позволяет перейти к алгебраическим уравнениям комплексной переменной при описании характеристик комплексных сопротивлений двухполюсников и передаточных функций четырехполюсников.

Ограничение количества пассивных элементов аналогового фильтра приводит к ограничению порядков интегро-дифференциальных уравнений и, соответственно, полиномов переменной при описании передаточных характеристик.

Прохождение сигнала через аналоговый фильтр описывается интегралом свертки входного сигнала и непрерывной импульсной характеристики , которая в свою очередь не может иметь произвольную форму при ограничении порядка аналогового фильтра, потому что является результатом решения интегро-дифференциальных уравнений ограниченного порядка.

Дискретные системы, в свою очередь, описываются разностными уравнениями дискретного времени . По аналогии с аналоговыми фильтрами, мы не можем требововать бесконечных порядков разностных уравнений, потому что это потребует бесконечных вычислительных ресурсов. Таким образом, мы должны ограничить порядки разностных уравнений, которые связывают выходной сигнал дискретного фильтра с входным сигналом , а также со значениями выходного сигнала на предыдущих тактах .

Заметим, что здесь мы также ведем рассмотрение относительно индексов отсчетов сигналов, в предположении c.

Общее разностное уравнение линейного цифрового фильтра имеет вид:

Временной индекс изменяется от до бесконечности, т.к. предполагается, что фильтр после включения может работать неограниченно долго.

Рассмотрим -преобразование разностного уравнения (16). -образ выходного сигнала равен:

Основы цифровой обработки сигналов: АЧХ и ФЧХ, Цифровые фильтры, КИХ и БИХ фильтры

Рассмотрены 3 темы по основам цифровой обработки сигналов: АЧХ и ФЧХ, цифровые фильтры, КИХ и БИХ фильтры

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

АЧХ и ФЧХ

В этом видео мы поговорим о таких характеристиках линейных стационарных систем, как амплитудно-частотная характеристика (АЧХ) и фазо-частотная характеристика (ФЧХ). В предыдущей публикации мы рассмотрели различные способы описания линейных стационарных дискретных систем. Разностное уравнение показывает, как вычислять значения отсчётов на выходе системы, передаточная функция описывает динамику в зэд области, импульсная характеристика нужна для свёртки с входным сигналом. Но ни одно из рассмотренных описаний не даёт нам понимания, как же именно наша система будет преобразовывать сигнал. А это хотелось бы знать до того, как мы подадим входное воздействие.

Именно поэтому для описания систем используют частотные характеристики. А именно – амплитудно-частотную характеристики (АЧХ) и фазочастотную характеристику (ФЧХ). Как вы уже поняли, это характеристики системы, но для их лучшего понимания мы можем обратиться к характеристикам сигнала.

Давайте для простоты начнём с АЧХ. У сигнала есть амплитудный спектр, то есть зависимость энергии сигнала в зависимости от частоты. А у системы есть АЧХ, говоря простыми словами, зависимость коэффициента усиления от частоты.

В частотной области спектр сигнала должен пройти через АЧХ системы, при этом его спектр исказится, подобно тому, как брусок пластилина изменит своё сечение при прохождении через определённую формочку.

Давайте рассмотрим влияние АЧХ и ФЧХ на отдельные спектральные составляющие сигнала, или синусоиды. Допустим, у нас есть сигнал, состоящий из двух отдельных синусоид. При прохождении через систему с АЧХ представленной формы, синусоида меньшей частоты не изменит своей амплитуды, в то время как синусоида большей частоты станет меньше по уровню, так как этой частоте соответствует коэффициентт усиления меньше единицы. АЧХ системы может усиливать сигнал в одних полосах и подавлять в других.

Фазочастотная характеристика показывает зависимость фазового сдвига от частоты. Подобно тому, как мы можем отразить фазовый спектр сигнала. Но в случае с ФЧХ, к начальной фазе сигнала на конкретной частоте добавится сдвиг, определяемый ФЧХ. Проще говоря, синусоида не только изменит свою амплитуду, но и сдвинется на временной оси.

АЧХ и ФЧХ наглядно демонстрируют нам, как система изменяет проходящий через неё сигнал. Но откуда мы получаем эти характеристики, и связанны ли они с разностным уравнением, или передаточной функцией? На самом деле да, связаны.

Если мы отобразим передаточную функцию на комплексной плоскости в виде трёхмерной поверхности, с учётом нулей и полюсов, и наложим на неё окружность единичного радиуса, то проекция или разворот этой кривой с учётом всех взлётов и падений и есть ни что иное, как форма амплитудно-частотной характеристики системы.

Как вы видите, кривая строится также и в области отрицательных частот. А о способах определения АЧХ системы я рекомендую Вам поискать дополнительную информацию самостоятельно.

Мы же подошли к основному смыслу рассматриваемых систем. Задачи линейных стационарных систем – изменять амплитуду и фазу входных сигналов. И процесс этот называется фильтрацией. К примеру, удаление нежелательной высокочастотной составляющей в сигнале и усиление полезной низкочастотной – типичная задача для линейной стационарной системы. Отныне и в дальнейшем мы будем называть такие системы фильтрами. И в следующих публикациях мы познакомимся с различными типами дискретных фильтров. Пока что нам важно усвоить, что для описания фильтра нам достаточно знать его коэффициенты a и b.

Давайте перейдём в MATLAB и проанализируем фильтр с коэффициентами из прошлой публикации.

Начнем мы с формирования входного воздействия. В нашем случае, это будет ЛЧМ сигнал, то есть так называемый сигнал с линейной частотной модуляцией. Давайте запустим секцию и посмотрим как он выглядит во временной области.

Вы видите, что это сигнал, у которого частота нарастает с ростом времени. Подобный тип сигнала позволит нам достаточно наглядно во временной области посмотреть на работу нашего фильтра.

Теперь давайте посмотрим, как же выглядит амплитудно-частотные и фазо-частотные характеристики при заданных коэффициентах b и a. Для этого мы воспользуемся встроенной функцией freqz. Это функция отображает сразу АЧХ и ФЧХ, также в этой секции мы высчитываем нули и полюса нашей передаточной функции и отображаем их на нуль-полюсной диаграмме. Из форм АЧХ мы сразу можем понять, что данный фильтр представляет собой фильтр нижних частот, то есть он пропускает частоты меньше 2 кГц, а начиная с 2 кГц он начинает постепенно подавлять, и высокочастотные компоненты будут уже гораздо меньше по уровню нежели низкочастотные. Нуль-полюсная диаграмма конечно не настолько наглядно показывает нам, что же будет происходить с сигналом при прохождении через наш фильтр.

В следующей секции мы будем строить трёхмерный вид передаточной функции на комплексной плоскости. Все длинные формулы вычисления я убрал в функцию helperfunk2, мы также будем прилагать её в описании к этому видео. Так что если хотите проанализировать ее, можете это сделать, но сейчас я на это время тратить не буду. Я просто запущу эту секцию, и мы посмотрим на вид нашей передаточной функции на комплексной плоскости.

Я специально отразил здесь 2 версии этой проекции, то есть в данном случае у нас здесь просто показаны 2 явных полюса и 1 ноль.

Если приблизить передаточную функцию, то мы явно увидим нашу кривую, которая при развороте даёт нам уже форму нашей АЧХ.

Если мы посмотрим на вид этого разворота, конкретно в области положительных частот, то он по форме очень напоминает то, что выдавала нам функция freqz. То есть здесь мы также наблюдаем АЧХ фильтра нижних частот.

Пришло время отфильтровать наш сигнал. Для этого мы воспользуемся встроенной функцией filter, которой мы просто передаём наши наборы коэффициентов фильтра и входное воздействие х. Затем мы отобразим отфильтрованный сигнал на одном графике с исходным. Давайте запустим эту секцию.

И как мы видим в момент времени t=1 сек, когда частота нашего сигнала доходит до 4 кГц, его амплитуда становится минимальной. Ну и завершении этого скрипта давайте попробуем вычислить выход нашего фильтра при помощи свертки. Для этого сперва мы вычисляем нашу импульсную характеристику фильтра при помощи встроенной функций impz, а затем при помощи функции conv определяем выход нашего фильтра.

В данном случае я накладываю выход функции filter и выход функции conv друг на друга. Как видите, они точно совпадают.

Цифровые фильтры

В этой публикации мы начинаем знакомиться с цифровыми фильтрами. В прошлых публикациях мы познакомились с описанием линейных стационарных дискретных систем, в данном и последующих видео мы будем знакомиться с применением подобных систем для задач цифровой обработки сигналов и фильтрации, в частности.

Для начала давайте вспомним, что делает фильтр в соответствии с задачами цифровой обработки. Например, он может пропускать сигналы в определённой полосе частот, и подавлять в других полосах. Он может быть частью эквалайзера, усиливая или подавляя сигнал в выбранной полосе. Помимо этого, фильтры могут быть использованы для изменения фазы сигнала, дифференцирования, изменения частоты дискретизации, но об этом мы пока не говорим. А сосредоточимся мы именно на свойствах частотной избирательности цифровых фильтров.

Давайте вспомним знакомый нам пример фильтра из предыдущих публикаций – скользящее среднее. Только в этот раз мы представим осредняющие коэффициенты как импульсную характеристику нашей линейной дискретной системы. Как ведёт себя подобный фильтр с точки зрения частотной избирательности? Давайте разберёмся в MATLAB.

В данном скрипте мы будем осуществлять осреднение входного сигнала, но теперь – через операцию свёртки сигнала с импульсной характеристикой линейной дискретной системы. Длина импульсной характеристики h может варьироваться через переменную num. Создаём сумму двух синусоид, медленной, которую мы считаем полезным сигналом, и быстрой, большей частоты и меньшей амплитуды, которая будет зашумлять первую. Сумму s мы затем сворачиваем с вектором h. Запускаем секцию скрипта и наблюдаем эффект осреднения входного сигнала.

Если импульсную характеристику сделать длиннее, то сигнал осредняется ещё сильнее, и задержка выхода относительно входа также увеличивается.

Но что здесь происходит с точки зрения частотной избирательности? Быстро меняющаяся синусоида подавляется, так как близко расположенные отсчёты входного сигнала приравниваются к среднему значению попавших в окно осреднения. Медленно изменяющийся сигнал при подобной операции искажается меньше, а это значит, что относительно плавно изменяющаяся первая синусоида на выходе подобного фильтра будет иметь большую амплитуду. С точки зрения частотной избирательности, подобная система пропускает сигналы меньшей частоты, и подавляет сигналы большей частоты.

Давайте убедимся в этом, оценив АЧХ фильтра. Воспользуемся функцией freqz. Как мы видим по форме АЧХ, это действительно фильтр нижних частот. В данной публикации мы рассмотрим параметры частотно-избирательных цифровых фильтров, и очертим основные этапы проектитования фильтров. И тут нужно сделать одно пояснение. Несмотря на то, что в предыдущих публикациях я говорил, что линейные дискретные системы мы можем смело называть фильтром, и часто в инженерных кругах так и делают, между ними всё же есть различие. Формально, линейной дискретной системой мы называем математическое описание, а фильтром – устройство. Фильтры строятся на основе описания линейной дискретной системы, но, помимо этого, также определяются способом их реализации – архитектурой, квантованием, платформой – например, цифровой фильтр может быть реализован программно, в виде кода, или аппаратно, как цифровая схема.

Давайте попробуем очертить основные параметры цифровых фильтров. Во-первых, сюда относятся параметры линейной дискретной системы, такие как передаточная функция или разностное уравнение, то есть по сути – коэффициенты фильтра. Тесно связанные с коэффициентами АЧХ и ФЧХ определяют функцию фильтра, например, тип его частотной избирательности, и об этом мы подробно поговорим в этом видео.

Импульсная характеристика также относится к параметрам линейной системы, но мы чаще говорим о классификации фильтров в зависимости от их импульсной характеристик. Мы различаем фильтры с конечной импульсной хар-кой – КИХ фильтры, и фильтры с бесконечной импульсной характеристикой – БИХ фильтры. О разнице между ними я расскажу с следующей публикации.

Помимо этого, у фильтров есть дополнительные характеристики, вытекающие из вышеперечисленных – например, переходная функция, групповая и фазовые задержки, нуль-полюсная диаграмма и прочие.

Фильтры могу различаться по своей архитектуре, а она тесно связана с реализацией устройства в железе. Также, большинство реальных фильтров работают в целочисленной арифметике, и при их реализации надо обязательно учитывать эффекты квантования.

Цифровые фильтры могут быть классифицированы по перечисленным характеристикам.

Давайте рассмотрим классификацию фильтров по их частотной избирательности, то есть по АЧХ. С точки зрения своей функции частотно-избирательной цепи, фильтры могут разделяться на множество типов. Рассмотрим основные, наиболее распространённые типы.

Во-первых, это фильтры нижних и верхних частот. Как вы понимаете из названия, фильтр нижних частот пропускает низкие частоты, до определённой частоты среза, и подавляет высокие частоты. Фильтр верхних частот исполняет обратную функцию.

Также существуют полосно-пропускающие и полосно-заграждающие фильтры. Первые пропускают сигнал только в определённой полосе частот, вторые могут подавлять сигнал в определённой полосе частот, и пропускать во всех остальных.

Ну и частным случаем полосовых фильтров могут считаться резонансные фильтры, пропускающие или подавляющие сигнал только на одной конкретной частоте.

Требования к частотной избирательности фильтра в зависимости от накладываемой на него задачи можно записать в виде спецификации к его частотным характеристикам.

Давайте познакомимся со спецификацией на примере фильтра нижних частот. У АЧХ подобного фильтра можно выделить три основные полосы, а именно – полосу пропускания, полосу перехода, и полосу заграждения.

Полоса пропускания фильтра, или passband, – это тот диапазон частот, в котором в идеале находится наш полезный сигнал. Его мы хотим пропустить по возможности без искажений. Границей полосы пропускания для ФНЧ является частота Fp, или Fpass. Она отсчитывается по уровню минус три децибела от максимума.

Усиление сигнала в полосе пропускания, опять-таки в идеале, должно быть постоянным. Но на практике зачастую присутствуют определённые нестабильности усиления, или пульсации. Уровень допустимых пульсаций в полосе пропускания определяется параметром Apass, и измеряется в децибелах.

Полоса заграждения, или stopband, – это тот диапазон частот, в котором сигнал должен гарантированно ослабляться не менее чем на Ast децибел. Начинается полоса заграждения с частоты Fst.

А между этими полосами находится переходная полоса, или transition band, усиление в этой полосе плавно спадает. Кстати, чем более резкий переход у фильтра от полосы пропускания к полосе заграждения, то есть чем уже полоса перехода, тем больший порядок должен иметь фильтр. А порядок – это количество коэффициентов фильтра, и оно связано с количеством умножителей, необходимых для реализации.

Так что фильтры с крутыми спадами обычно более сложные и дорогие, поэтому перед проектировщиком всегда стоит задача поиска компромисса между соответствием формы частотной характеристики некой идеальной, и стоимостью реализации устройства.

Давайте также рассмотрим этапы проектирования того самого устройства – цифрового фильтра. Начинаем мы с определения спецификации фильтра, исходя из его задачи. Затем нам надо понять, хотим мы использовать для этого КИХ или БИХ фильтр. Как и говорил, о разнице между ними – в следующей публикации. Затем нам необходимо на основе спецификации и типа фильтра подсчитать коэффициенты, то есть те значения, на которые мы будем умножать отсчёты входного и, возможно, выходного сигналов.

Процесс, который является ключевым здесь – переход от спецификации к коэффициентам! Сложная в прошлом вычислительная задача в современном мире решается очень просто – при помощи MATLAB. Большинство инженеров занимаются расчётом коэффициентов фильтров именно в MATLAB с использованием средств Signal Processing Toolbox.

Давайте пройдём путь до подсчёта коэффициентов по заданной спецификации в livescript, пока что не затрагивая реализацию. Для начала импортируем и прослушаем аудиофайл, который будет нашим входным сигналом.

Затем перейдём к спецификации.

Я хочу попробовать создать полосно-заграждающий фильтр, который слегка подавит так называемую середину. Полоса заграждения будет лежать в пределах от 1000 до 4000 Гц. Подавление в полосе будет всего лишь 10 дБ, а уровень допустимых пульсаций в полосах пропускания составит 1 дБ. Для аудио-фильтра это весьма много, но для нашего примера это не так критично.

Затем мы формируем объект спецификации d. Для этого мы передаём функции fdesign тип отклика – bandstop, и все наши значения параметров.

Затем на основе объекта спецификации мы уже будем счиать коэффициенты, которые будут храниться в объекте фильтра Hd . Подсчитываем мы их командой design. Ей мы передаём объект спецификации и тип фильтра. У нас это КИХ фильтр типа equiripple.

На основе подсчитанных коэффициентов MATLAB вычисляет характеристики фильтра и мы можем их посмотреть в программе Filtel Visualization Tool.

Здесь мы сразу наглядно оцениваем АЧХ фильтра и соответствие её спецификации. Маска спецификации отрисовывается красными пунктирными линиями. Так же нам доступны выизуализации фазочастотной характеристики, групповой и фазовой задержек, импульсной и переходной характеристик, нуль-полюсная диаграмма, значения коэффициентов и сводная информация, включающая также стоимость реализации фильтра.

Если мы отразим значения коэффициентов числителя передаточной функции фильтра на графике, то мы можем заметить, что это – импульсная характеристика.

Для КИХ-фильтров это всегда так, но подробнее об этом мы поговорим в следующей публикации.

А сейчас нам осталось только применить фильтр к входному аудиофайлу и прослушать результат. Ну а если вам интересно посмотреть на спектр сигнала до и после фильтрации – попробуйте сделать это самостоятельно, команды вы знаете. Просто добавьте их в livescript.

КИХ и БИХ фильтры

В данной публикации мы поговорим о КИХ и БИХ фильтрах, о разнице между ними и мотивациях применения. Начнём с КИХ-фильтров. По определению, КИХ – это фильтр с конечной импульсной характеристикой. По английский это произносится как FIR Filter, от final impulse response. КИХ фильтры – нерекурсивные, а это значит, что для вычисления значения на выходе фильтра используются только текущее и задержанные значения входа. В разностном уравнении есть только коэффициенты при x. Передаточная функция в знаменателе имеет константу, часто единицу. А схема фильтра не имеет обратных связей.

Если вы вспомните схему для подсчёта дискретной свёртки из предыдущих публикаций, то она очень похожа на представленную схему КИХ-фильтра. Вектор входных отсчётов формируется при помощи линий задержки, или регистров, перемножение отсчётов сигнала на отсчёты импульсной характеристики осуществляется в умножителях, а сумматоры потом объединяют всё в отсчёт выходного сигнала. Отсчёты импульсной характеристики КИХ-фильтра – это и есть вектор коэффициентов b. То есть мы указываем импульсную характеристику явно, и она по понятным причинам конечна.

Теперь поговорим о преимуществах и недостатках применения КИХ-фильтров.

Начнём с преимуществ:

• они могут обладать линейной фазой, и это очень важно, так как задача компенсации фазового набега заметно упрощается;
• они всегда устойчивы, то есть даже при очень большом уровне входного сигнала при его выключении через некоторое время сигнал на выходе гарантированно затухнет. Это прямое следствие того, что схемы КИХ-фильтров не содержат обратных связей
• ну и фактически имея достаточный порядок фильтра, мы можем сформировать произвольный частотный или фазовый отклик

Основной существенный недостаток КИХ-фильтров:

• Они до роже в реализации, чем БИХ-фильтры со схожей АЧХ.

Мы говорим, что КИХ-фильтры обычно бывают больших порядков, а порядок фильтра влияет на количество ресурсов, требуемых для его реализации. О каких ресурсах мы говорим? Когда мы рассматриваем аппаратную реализацию, то есть цифровую схему, то речь идёт о базовых блоках для построения фильтров – умножителях, сумматорах и регистрах, или линиях задержки. Иногда там ещё используются мультиплексоры.

Кратко расскажу об одном из методов синтеза КИХ-фильтров, наиболее наглядном. Под синтезом мы понимаем процесс получения коэффициентов. И так как коэффициенты КИХ-фильтра – это его импульсная характеристика, то мы можем нарисовать идеальную форму АЧХ, (к примеру, здесь мы идём от идеальной АЧХ фильтра нижних частот) и при помощи обратного быстрого преобразования Фурье получить соответствующую ей идеальную импульсную характеристику. Она получится бесконечная.

Затем эту импульсную характеристику мы перемножаем с оконной функцией конечной длительности, то есть формируем конечную импульсную характеристику. При ограничении количества отсчётов, форма АЧХ отклоняется от идеальной, появляются пульсации и переходные полосы. Вспоминаем эффект Гиббса. А вообще методы синтеза фильтров – это отдельная наука, в рамках данного курса мы её не охватим.

А в рамках этой публикации мы познакомимся с БИХ-фильтрами, фильтрами с бесконечной импульсной характеристикой. По-английски они называются IIR (Infinite impulse response). Кстати, БИХ-фильтры могут быть как аналоговые, так и цифровые. КИХ-фильтры могут быть только цифровыми.

БИХ фильтры – рекурсивные, для вычисления значения на выходе фильтра используются как значения входа, так и задержанные значения выхода. Передаточная функция представляется в стандартном дробно-рационально виде, а схема фильтра содержит обратные связи.

Из преимуществ БИХ-фильтров можно отметить:

• относительную простоту реализации по сравнению с КИХ-фильтрами (мы убедимся в этом на примере),
• относительную простоту синтеза на основе аналоговых прототипов.

В качестве недостатков:

• могут быть неустойчивыми. Если коэффициент в цепи обратной связи будет больше единицы, может образоваться положительная обратная связь, фильтр может завестись, и сигнал на его выходе может продолжаться и усиливаться даже после выключения входного воздействия,
• они не могут обладать линейной фазой,
• мы не можем сформировать произвольную АЧХ и ФЧХ, по сути, мы выбираем АЧХ из типов, основывающихся на аналоговых прототипах, чаще всего это стандартные фильтры нижних и верхних частот, полосовые и так далее. Частотно-избирательные фильтры, с полосами пропускания и заграждения и без какого-либо контроля над фазой сигнала.

Синтезируются БИХ-фильтры при помощи преобразования непрерывной передаточной характеристики аналогового прототипа в дискретную характеристику цифрового фильтра. В детали билинейного преобразования тоже не лезем.

А поговорим мы про автоматизацию задания спецификации и синтеза самых разнообразных фильтров в MATLAB. Конкретно – про интерактивное приложение Filter Designer App, ранее называлось FDA Tool. Это приложение в составе Signal Processing Toolbox для анализа, синтеза, квантования фильтров, создания многоскоростных систем, импорта и экспорта коэффициентов и многого другого. Инженеры по всему миру не один десяток лет используют именно это приложение для быстрого проектирования цифровых фильтров, очень его любят и уважают, вполне заслуженно.

Давайте воспользуемся им для фильтрации зашумлённого музыкального файла. Во-первых, загрузим аудиоданные. Я это сделаю, просто кликнув дважды по mp3-файлу. Именя переменных оставляем по-умолчанию. Ну и сразу прослушаем аудио. Мы слышим Дебюсси с наложенными на него ударными из другой композиции.

Посмотрим на этот сигнал в Signal Analyzer. Выберем наш вектор, отобразим его во временной области, укажем частоту дискретизации, чтобы наблюдать сигнал в реальных секундах и герцах. И отобразим спектр.

Курсор поможет нам понять, где проходит граница полезного сигнала и помехи. Граница расположена в районе 2.2 кГц. Свернём Signal Analyzer и откроем инструмент Filter Designer. Попробуем разработать в нём подходящий цифровой фильтр.

Выбираем тип отклика мы оставляем lowpass, то есть фильтр нижних частот. Пока что попробуем реализовать его в виде КИХ-фильтра equiripple. Указываем частоту дискретизации, границу полосы пропускания и начало полосы заграждения. На переходную полосу мы оставляем всего лишь 200 Герц, это достаточно крутой спад. Пульсации для аудио-фильтра мы зададим не более 0.1 децибела, а подавление оставим на уровне 80. Нажимаем кнопку Design Filter.

И наблюдаем АЧХ. Форма вполне соответствует спецификации, фазочастотная характеристика линейна в полосе пропускания, групповая и фазовая задержки – константы, тут же можем оценить форму импульсной характеристики и переходной функции,

Но на вкладке информации мы можем увидеть, что фильтр требует очень много ресурсов, более семи сотен умножителей, сумматоров и регистров.

Проверим, будет ли БИХ-фильтр экономичнее. Выберем самый экономичный вариант, эллиптический БИХ-фильтр, наблюдаем форму его АЧХ, и в информации видим, что ресурсов подобный фильтр требует в тридцать раз меньше! Это серьёзная разница.

Но за неё придётся поплатиться нелинейностью фазы, а также зависящими от частоты групповой и фазовой задержками. Но наш БИХ-фильтр устойчив, все его полюса находятся внутри окружности единичного радиуса на нуль-полюсной диаграмме.

И в информации о структуре фильтра мы видим надпись Second Order Sections. Покажем структуру в центре документации.

Секции второго порядка – это каскадный способ построения БИХ-фильтров из меньших фильтров второго порядка. Оставим всё как есть, убедимся, что форма АЧХ нас устраивает, а фаза для задачи фильтрации аудио не так критична.

И теперь мы экспортируем вычисленные коэффициенты фильтра в рабочее пространство MATLAB в виде так называемой sos матрицы и вектора усилений для каждого каскада. Каждая секция содержит шесть коэффициентов, они объединяются в матрицу размером n на 6. При желании мы можем преобразовать такую форму преставления в привычные нам коэффициенты передаточной функции. Воспользуемся функцией sos2tf и получим общую дробь для всего фильтра. Теперь отфильтруем входной сигнал data, и оценим результат в Signal Analyzer. Добавим вектор y, укажем ему частоту дискретизации, чтобы на временной оси его можно было отрисовать.

Видим явное уменьшение амплитуды на всём промежутке, и на спектре после 2,2 кГц мы наблюдаем серьёзное подавление. Проверим, удалось ли нам освободить Дебюсси. Прослушаем выход фильтра командой sound. В целом, получилось неплохо.