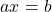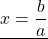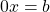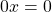Как определить сколько корней имеет линейное уравнение

Что такое линейное уравнение

Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?

В курсе алгебры 7 класса линейное уравнение определяется следующим образом.

Определение.

Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.

Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.

Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:

Количество корней линейного уравнения зависит от значения a (коэффициента перед x).

При a≠0 линейное уравнение имеет единственное решение.

Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:

Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).

В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).

При a=0, b≠0 линейное уравнение

При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.

При a=0, b=0 линейное уравнение

имеет бесконечное множество решений.

При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.

Возможные решения линейных уравнений можно изобразить в виде схемы.

Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.

Решение многих уравнений сводится к решению линейных уравнений.

Как решать линейные уравнения с одной переменной

Линейное уравнение с одной переменной — общие сведения

С темой уравнений можно познакомиться на первых уроках алгебры. В школьном курсе предложено такое объяснение: уравнение является равенством с неизвестным, которое необходимо вычислить. Неизвестное, или переменную, принято обозначать с помощью латинских букв.

Уравнение является математическим равенством с одной или несколькими неизвестными величинами.

Значение неизвестных определяется так, чтобы при подстановке в уравнение оно обращало его в верное числовое равенство.

Рассмотрим следующее выражение:

Если посчитать значение левой части, уравнение станет верным числовым равенством, то есть:

Еще одно выражение:

Здесь имеется некая переменная х, которую нужно вычислить. Уравнение в этом случае станет справедливым равенством, если найденное значение х оправдает знак равенства. Тогда левая часть выражения станет равна правой части.

Специфика преобразований при работе с алгебраическими уравнениями состоит в том, чтобы оставить слева в выражении многочлен от неизвестных, а правую часть обратить в ноль.

Линейное уравнение — это уравнение, записанное в виде:

где а и b являются действительными числами.

Корень уравнения, сколько их всего

Корень уравнения является таким числом, которое при подстановке на место неизвестной уравнивает правую и левую части выражения.

Решить уравнение — определить все из возможных его корней, либо доказать их отсутствие.

Принципы поиска корней уравнения ах + b = 0:

• при а, отличном от нуля, уравнение имеет только один корень;
• когда а имеет нулевое значение, уравнение не имеет корней;
• если а и b равны нулю, тогда корнем уравнения является любое число.

Как решать, описание алгоритма

Правило переноса: если требуется перенести член из одной части уравнения в другую, то нужно изменить знак этого члена на противоположный.

Рассмотрим действие данного правила на примере:

Заметим, что в уравнении имеется пара частей:

• (х + 3) является левой частью;
• 5 — это правая часть.

Переместим число 3 вправо, изменив его знак на противоположный:

В итоге получилось верное числовое равенство. Это значит, что корень определен правильно.

Разберем еще одно уравнение:

Переместим член 5х влево с заменой знака на противоположный:

После приведения подобных вычислим х:

Правило деления: обе части любого уравнения допускается делить на одно и то же число.

Рассмотрим применение этого правила на практике:

Здесь при неизвестном записан числовой коэффициент в виде числа 4. Преобразуем уравнение так, чтобы числовой коэффициент при х стал равным единице. Для этого нужно поделить обе части уравнения на число 4:

Далее выполним сокращение дробей и найдем корень уравнения:

Разберем вариант, когда перед неизвестной переменной стоит знак минуса:

Выполним сокращение обеих частей уравнения на число -4:

Когда перед скобками стоит знак минуса, который необходимо исключить, следует изменить знаки внутри скобок на противоположные. В результате при вычислениях не будет допущена ошибка, что особенно важно при решении заданий на системы уравнений, примеров с разным количеством неизвестных.

Стандартный алгоритм решения линейных уравнений:

1. Раскрыть скобки при их наличии.
2. Сгруппировать члены с неизвестной переменной в одной части уравнения. Остальные члены должны остаться в другой части уравнения.
3. Привести подобные в обеих частях уравнения.
4. Решить уравнение вида aх = b, разделив обе части уравнения на числовой коэффициент a при неизвестном x.

Упростить решение задач на линейные уравнения можно методом использования следующей схемы:

Примеры задач для 7 класса с объяснением

Найти корни уравнения:

Перенесем единицу вправо, изменив знак на отрицательный:

Далее разделим уравнение на число 6, которое является общим множителем:

Требуется решить уравнение:

5 ( х − 3 ) + 2 = 3 ( х − 4 ) + 2 х − 1

В первую очередь избавимся от скобок:

5 х − 15 + 2 = 3 х − 12 + 2 х − 1

Далее сгруппируем члены уравнения, руководствуясь стандартным алгоритмом решения линейных уравнений:

5 х − 3 х − 2 х = 0 − 12 − 1 + 15 − 2

Затем следует привести подобные:

Ответ: х является любым числом.

Нужно вычислить неизвестную х :

Выполним вычисления по правилу деления:

Найти решение уравнения:

4 ( х + 2 ) = 6 − 7 х

Выполним вычисления, руководствуясь стандартным алгоритмом решения линейных уравнений:

Вычислить корни уравнения:

3 x — 4 4 = 7 x 3 + 2

Выполним вычисления, руководствуясь стандартным алгоритмом решения линейных уравнений:

12 × 3 x — 4 4 = 12 × 7 x 3 + 12 × 2

3 ( 3 x — 4 ) = 4 × 7 х + 24

9 х – 12 = 28 х + 24

9 х – 28 х = 24 + 12

Решить линейное уравнение:

В первую очередь избавимся от скобок:

5 х − 15 + 2 = 3 х − 2 + 2 х − 1

Затем выполним группировку членов с неизвестными, а справа оставим свободные члены:

Ответ: данное уравнение не имеет решений.

Решить линейное уравнение:

2 ( х + 3 ) = 5 − 7 х

Выполним вычисления, согласно стандартному алгоритму решения линейных уравнений:

Решение линейных уравнений с одной переменной

В данной статье рассмотрим принцип решения таких уравнений как линейные уравнения. Запишем определение этих уравнений, зададим общий вид. Разберем все условия нахождения решений линейных уравнений, используя, в том числе, практические примеры.

Обратим внимание, что материал ниже содержит информацию по линейным уравнениям с одной переменной. Линейные уравнения с двумя переменными рассматриваются в отдельной статье.

Что такое линейное уравнение

Линейное уравнение – это уравнение, запись которого такова:
a · x = b , где x – переменная, a и b – некоторые числа.

Такая формулировка использована в учебнике алгебры ( 7 класс) Ю.Н.Макарычева.

Примерами линейных уравнений будут:

3 · x = 11 (уравнение с одной переменной x при а = 5 и b = 10 );

− 3 , 1 · y = 0 (линейное уравнение с переменной y, где а = — 3 , 1 и b = 0 );

x = − 4 и − x = 5 , 37 (линейные уравнения, где число a записано в явном виде и равно 1 и — 1 соответственно. Для первого уравнения b = — 4 ; для второго — b = 5 , 37 ) и т.п.

В различных учебных материалах могут встречаться разные определения. К примеру, Виленкин Н.Я. к линейным относит также те уравнения, которые возможно преобразовать в вид a · x = b при помощи переноса слагаемых из одной части в другую со сменой знака и приведения подобных слагаемых. Если следовать такой трактовке, уравнение 5 · x = 2 · x + 6 – также линейное.

А вот учебник алгебры ( 7 класс) Мордковича А.Г. задает такое описание:

Линейное уравнение с одной переменной x – это уравнение вида a · x + b = 0 , где a и b – некоторые числа, называемые коэффициентами линейного уравнения.

Примером линейных уравнений подобного вида могут быть:

3 · x − 7 = 0 ( a = 3 , b = − 7 ) ;

1 , 8 · y + 7 , 9 = 0 ( a = 1 , 8 , b = 7 , 9 ) .

Но также там приведены примеры линейных уравнений, которые мы уже использовали выше: вида a · x = b , например, 6 · x = 35 .

Мы сразу условимся, что в данной статье под линейным уравнением с одной переменной мы будем понимать уравнение записи a · x + b = 0 , где x – переменная; a , b – коэффициенты. Подобная форма линейного уравнения нам видится наиболее оправданной, поскольку линейные уравнения – это алгебраические уравнения первой степени. А прочие уравнения, указанные выше, и уравнения, приведенные равносильными преобразованиями в вид a · x + b = 0 , определим, как уравнения, сводящиеся к линейным уравнениям.

При таком подходе уравнение 5 · x + 8 = 0 – линейное, а 5 · x = − 8 — уравнение, сводящееся к линейному.

Принцип решения линейных уравнений

Рассмотрим, как определить, будет ли заданное линейное уравнение иметь корни и, если да, то сколько и как их определить.

Факт наличия корней линейного уравнения определятся значениями коэффициентов a и b . Запишем эти условия:

• при a ≠ 0 линейное уравнение имеет единственный корень x = — b a ;
• при a = 0 и b ≠ 0 линейное уравнение не имеет корней;
• при a = 0 и b = 0 линейное уравнение имеет бесконечно много корней. По сути в данном случае любое число может стать корнем линейного уравнения.

Дадим пояснение. Нам известно, что в процессе решения уравнения возможно осуществлять преобразование заданного уравнения в равносильное ему, а значит имеющее те же корни, что исходное уравнение, или также не имеющее корней. Мы можем производить следующие равносильные преобразования:

• перенести слагаемое из одной части в другую, сменив знак на противоположный;
• умножить или разделить обе части уравнения на одно и то же число, не равное нулю.

Таким образом, преобразуем линейное уравнение a · x + b = 0 , перенеся слагаемое b из левой части в правую часть со сменой знака. Получим: a · x = − b .

Далее мы разделим обе части равенства на число а , при этом условившись, что это число отлично от нуля, иначе деление станет невозможным. Случай, когда а = 0 , рассмотрим позже.

Итак, производим деление обеих частей уравнения на не равное нулю число а, получив в итоге равенство вида x = — b a . Т.е., когда a ≠ 0 , исходное уравнение a · x + b = 0 равносильно равенству x = — b a , в котором очевиден корень — b a .

Методом от противного возможно продемонстрировать, что найденный корень – единственный. Зададим обозначение найденного корня — b a как x 1 . Выскажем предположение, что имеется еще один корень линейного уравнения с обозначением x 2 . И конечно: x 2 ≠ x 1 , а это, в свою очередь, опираясь на определение равных чисел через разность, равносильно условию x 1 − x 2 ≠ 0 . С учетом вышесказанного мы можем составить следующие равенства, подставив корни:
a · x 1 + b = 0 и a · x 2 + b = 0 .
Свойство числовых равенств дает возможность произвести почленное вычитание частей равенств:

a · x 1 + b − ( a · x 2 + b ) = 0 − 0 , отсюда: a · ( x 1 − x 2 ) + ( b − b ) = 0 и далее a · ( x 1 − x 2 ) = 0 . Равенство a · ( x 1 − x 2 ) = 0 является неверным, поскольку ранее условием было задано, что a ≠ 0 и x 1 − x 2 ≠ 0 . Полученное противоречие и служит доказательством того, что при a ≠ 0 линейное уравнение a · x + b = 0 имеет лишь один корень.

Обоснуем еще два пункта условий, содержащие a = 0 .

Когда a = 0 линейное уравнение a · x + b = 0 запишется как 0 · x + b = 0 . Свойство умножения числа на нуль дает нам право утверждать, что какое бы число не было взято в качестве x, подставив его в равенство 0 · x + b = 0 , получим b = 0 . Равенство справедливо при b = 0 ; в прочих случаях, когда b ≠ 0 , равенство становится неверным.

Таким образом, когда a = 0 и b = 0 , любое число может стать корнем линейного уравнения a · x + b = 0 , поскольку при выполнении этих условий, подставляя вместо x любое число, получаем верное числовое равенство 0 = 0 . Когда же a = 0 и b ≠ 0 линейное уравнение a · x + b = 0 вовсе не будет иметь корней, поскольку при выполнении указанных условий, подставляя вместо x любое число, получаем неверное числовое равенство b = 0 .

Все приведенные рассуждения дают нам возможность записать алгоритм, дающий возможность найти решение любого линейного уравнения:

• по виду записи определяем значения коэффициентов a и b и анализируем их;
• при a = 0 и b = 0 уравнение будет иметь бесконечно много корней, т.е. любое число станет корнем заданного уравнения;
• при a = 0 и b ≠ 0 заданное уравнение не будет иметь корней;
• при a , отличном от нуля, начинаем поиск единственного корня исходного линейного уравнения:

1. перенесем коэффициент b в правую часть со сменой знака на противоположный, приводя линейное уравнение к виду a · x = − b ;
2. обе части полученного равенства делим на число a , что даст нам искомый корень заданного уравнения: x = — b a .

Собственно, описанная последовательность действий и есть ответ на вопрос, как находить решение линейного уравнения.

Напоследок уточним, что уравнения вида a · x = b решаются по похожему алгоритму с единственным отличием, что число b в такой записи уже перенесено в нужную часть уравнения, и при a ≠ 0 можно сразу выполнять деление частей уравнения на число a .

Таким образом, чтобы найти решение уравнения a · x = b , используем такой алгоритм:

• при a = 0 и b = 0 уравнение будет иметь бесконечно много корней, т.е. любое число может стать его корнем;
• при a = 0 и b ≠ 0 заданное уравнение не будет иметь корней;
• при a , не равном нулю, обе части уравнения делятся на число a , что дает возможность найти единственный корень, который равен b a .

Примеры решения линейных уравнений

Необходимо решить линейное уравнение 0 · x − 0 = 0 .

Решение

По записи заданного уравнения мы видим, что a = 0 и b = − 0 (или b = 0 , что то же самое). Таким образом, заданное уравнение может иметь бесконечно много корней или любое число.

Ответ: x – любое число.