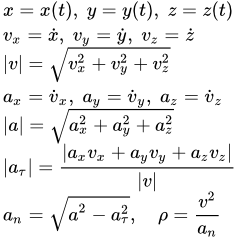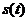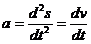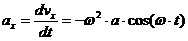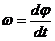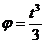Координатный способ задания движения точки
Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
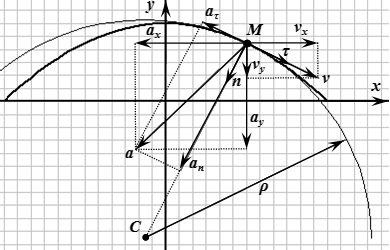
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
Определение скорости и ускорения точки.
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Ускорение точки – векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
Задание скорости и ускорения точки естественным способом
При задании точки естественным способом известен закон движения, выраженный зависимостью перемещения точки от времени
В этом случае скорость точки будет определяться как первая производная от данной зависимости
Ускорение точки будет определяться как вторая производная от зависимости перемещения или как первая производная от зависимости скорости
Точка движется по окружности радиусом R согласно уравнению.
Определить скорость и ускорение точки в конце 3 секунды

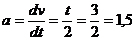
Задание скорости точки координатным способом
При задании точки координатным способом известны законы изменения координат данной точки в зависимости от времени 
В этом случае скорость точки будет определяться как геометрическая сумма первых производных от данных зависимостей

Ускорение точки будет определяться как геометрическая сумма первых производных от зависимостей скорости или вторых производных от зависимости изменения координат

Уравнения движения точки имеют вид
Определить уравнения скорости и ускорения данной точки
Если направление ускорения совпадает с направлением скорости (имеет одинаковый знак) то тело движется с положительным ускорением (ускоряется), если направление ускорения не совпадает с направлением скорости (имеет разные знаки) то тело движется с отрицательным ускорением (замедляется)
Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Все точки твердого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести С.
Для описания скорости и ускорения точки используются зависимости рассмотренные в предыдущем вопросе.
Вращательное движение
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.
Аналогом перемещения во вращательном движении является угол поворота 
Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростьютела.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорениемтела.
Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением. При этом, если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается —равнозамедленным.
Рассмотрим движение точки М тела движущуюся по окружности с радиусом R.
Обозначим точку отсчета О, и угол, на который повернется эта точка за время t через 
За время t точка М пройдет расстояние s равное длине дуги окружности ОМ. Это расстояние определяется по формуле.
Скорость точки М в момент времени t при вращательном движении направлена по касательной к окружности в этой точке и называется окружной скоростью.
Величина окружной скорости определяется из выражения.
Из предыдущей формулы следует, что модули окружных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Ускорение точки М в момент времени t при вращательном движении складывается из двух составляющих вращательного ускорения (тангенциального) и центростремительного ускорения (нормального).
Тангенциальное ускорение направлено по касательной к окружности в точке М.
Величина тангенциального ускорения определяется по зависимости
Нормальное ускорение направлено по радиусу окружности к её центру.
Величина нормального ускорения определяется по зависимости
Полное ускорение точки определится из выражения
Вращение маховика в период пуска машины определяется уравнением
где t — в сек, 
По уравнению вращения маховика находим его угловые скорость и ускорение
Определяем уравнение окружной скорости точки
Выражаем отсюда время

Угловая скорость 
Угловое ускорение 
Тангенциальное ускорение 
Нормальное ускорение 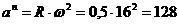
Полное ускорение 
Скорость и ускорение точки
Механическим движением называют изменение с течением времени положения в пространстве точек и тел относительно какого-либо основного тела, с которым скреплена система отсчета. Кинематика изучает механическое движение точек и тел независимо от сил, вызывающих эти движения. Всякое движение, как и покой, относительно и зависит от выбора системы отсчета.
Траекторией точки называют непрерывную линию, описывае мую движущейся точкой. Если траектория — прямая линия, то движение точки называют прямолинейным, а если — кривая, то — криволинейным. Если траектория — плоская, то движение точки называют плоским.
Движение точки или тела, считается заданным или известным, если для каждого момента времени (t) можно указать положение точки или тела относительно выбранной системы координат.
Положение точки в пространстве определяется заданием:
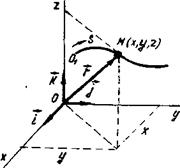 |
а) траектории точки;
б) начала О1 отсчета расстояния по траектории (Рисунок 11): s = О1М — криволинейная координата точки М;
в) направления положи тельного отсчета расстояний s;
г) уравнения или закона движения точки по траектории: S = s(t)
Скорость точки. Если точка за равные промежутки времени проходит равные отрезки пути, то ее движение называют равномерным. Скорость равномерного движения измеряется отношением пути з, пройденного точкой за некоторый промежуток времени, к величине этого промежутка времени: v = s/1. Если точка за равные промежутки времени проходит неравные пути, то ее движение называют неравномерным. Скорость в этом случае также переменна и является функцией времени: v = v(t). Рассмотрим точку А, которая перемещается по заданной траектории по некоторому закону s = s(t) (Рисунок 12):
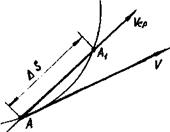 |
За промежуток времени t т. А переместилась в положение А1 по дуге АА. Если промежуток времени Δt мал, то дугу АА1 можно заменить хордой и найти в первом приближении величину средней скорости движения точки vcp = Ds/Dt. Средняя скорость направлена по хорде от т. А к т. А1.
Истинная скорость точки направлена по касательной к траектории, а ее алгебраическая величина определяется первой производной пути по времени:
v = limΔs/Δt = ds/dt
Размерность скорости точки: (v) = длима/время, например, м/с. Если точка движется в сторону увеличения криволинейной координаты s, то ds > 0, и следовательно, v > 0, а в противном случае ds
Нормальное ускорение характеризует изменение скорости по
направлению.
Величина полного ускорения: 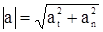
Виды движения точки в зависимости от ускорения.
Равномерное прямолинейное движение (движение по инерции) характеризуется тем, что скорость движения постоянна, а радиус кривизны траектории равен бесконечности.
То есть, r = ¥, v = const, тогда 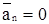
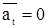
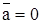
Прямолинейное неравномерное движение. Радиус кривизны траектории r = ¥, аn = 0, поэтому 
Криволинейное равномерное движение. Поскольку v = const, то аt = dv/dt = 0; 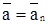
Движение точки, при котором величина касательного ускорения постоянна (аt = соnst) называют равнопеременным. Величину ускорения можно также определить через значение скорости в начале и в конце произвольного промежутка времени t: at = (v – v0)/t, откуда v = v0 + at·t. Путь, пройденный точкой при равнопеременном движении, определится по уравнению:
Примером равномерно-ускоренного движения может служить свободное падение тела, при этом ускорение свободного падения тел вблизи поверхности Земли составляет в среднем g = 9,81 м/с 2 .
Дата добавления: 2015-08-08 ; просмотров: 7034 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://lektsii.org/17-8319.html
http://helpiks.org/4-65709.html