Тригонометрические уравнения и преобразования
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | $<π>/<6>$ | $<π>/<4>$ | $<π>/<3>$ | $<π>/<2>$ | $π$ |
| $sinα$ | $ 0$ | $ <1>/<2>$ | $ <√2>/<2>$ | $ <√3>/<2>$ | $ 1$ | $ 0$ |
| $cosα$ | $ 1$ | $ <√3>/<2>$ | $ <√2>/<2>$ | $ <1>/<2>$ | $ 0$ | $ -1$ |
| $tgα$ | $ 0$ | $ <√3>/<3>$ | $ 1$ | $ √3$ | $ -$ | $ 0$ |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ <√3>/<3>$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ ($<π>/<2>$ и $<3π>/<2>$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα=
/ $ - $ctgα=
/ $ - $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = <5>/ <13>; t ∈(<3π>/<2>;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(<3π>/<2>;2π)$ -это четвертая четверть, то синус в ней имеет знак минус
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .
Обозначение: sin α = y ; cos α = x ; tg α = y : x .
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
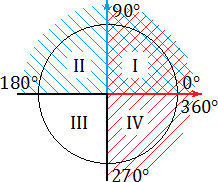
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
- cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
http://www.berdov.com/ege/trigonometry/sign/
http://epmat.ru/modul-geometriya/urok-1-trigonometriya/