Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Высшая математика.
- Аналитическая геометрия.
- Уравнение эллипса, гиперболы, параболы в полярной системе координат.
Уравнение эллипса, гиперболы, параболы в полярной системе координат.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Пример.
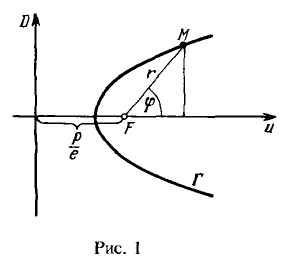
Пусть $\Gamma -$ эллипс, ветвь гиперболы или парабола, $F -$ фокус этой кривой, $D -$ соответствующая директриса. Вывести уравнение кривой $\Gamma$ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1).
Решение.
Общее свойство эллипса, гиперболы и параболы состоит в следующем $$M\in\Gamma\Leftrightarrow\frac<\rho(M, F)><\rho(M, D)>=const=e,\qquad\qquad (1)$$ где $e -$ эксцентриситет кривой ( $e 1$ для гиперболы и $e=1$ для параболы)
Обозначим расстояние от фокусы до директрисы через $\frac
<1-e\cos\varphi>.\qquad\qquad (2)$$ Уравнение (2) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы. Примеры. 2.321(а). Для эллипса $\frac Решение. Найдем эксцентриситет параболы и параметр $p:$ Далее, подставляя найденные параметры в полярное уравнение (2), найденное в предыдущей задаче, найдем уравнение данного эллипса: 2.324(а). Написать каноническое уравнение кривой второго порядка $r=\frac<9><5-4\cos\varphi>.$ Решение. Приведем заданное уравнение, к уравнению вида $r=\frac <1-e\cos\varphi>:$ Отсюда имеем: $e=\frac<4><5>,$ $p=\frac<9><5>.$ Поскольку $e Далее, подставляя выражения эксцентриситета и параметра по определению, надем полуоси эллипса: Таким образом, запишем каноническое уравнение эллипса: Вывести полярное уравнение гиперболы $\frac Решение. Так как полюс находится в центре гиперболы, то $OM=r,$ тогда $\rho(M, D)=r\cos\varphi-\frac Таким образом, из уравнения (1) находим: Домашнее задание. 2.321(б) Для эллипса $\frac 2.322. Для правой ветви гиперболы $\frac а) в левом фокусе, б) в правом фокусе. 2.323. Для параболы $y^2=6x$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в фокусе параболы. 2.324 (б, в) Написать канонические уравнения следующих кривых второго порядка: Ответ: а) $\frac 2.327. Вывести полярное уравнение параболы $y^2=2px$ при условии, что полярная ось сонаправленна с осью $Ox,$ а полюс находится в вершине параболы. Вы будете перенаправлены на Автор24 На плоскости, кроме декартовой прямоугольной системы координат, используют также полярную систему координат. Это связано с тем, что сложность уравнений кривых зависит от системы координат, в которой они представляются. Поэтому при удачном выборе системы координат можно существенно упростить решение той или иной задачи. Уравнение окружности радиуса $R$ с центром в начале координат в декартовой системе координат имеет вид: $x^ <2>+y^ <2>=R^ <2>$. Уравнение той же окружности в полярной системе координат: $\rho =R$. Полярная система координат вводится следующим образом. На плоскости вибираем некоторую точку $O$, которая называется полюсом. Из этой точки проводим луч $Ox$, который называется полярной осью. Выбираем линейный масштаб для измерения длин отрезков. Для измерения углов выбираем или градусную, или радианную меру. Положение точки $M$ на плоскости определяют два числа: число $\rho $ — расстояние точки $M$ от полюса (полярный радиус $OM$), а также число $\phi $ — угол, образованный полярным радиусом с полярной осью (полярный угол). Положительным направлением отсчета угла $\phi $ считается направление против часовой стрелки. Числа $\rho $ и $\phi $ называются полярными координатами точки $M\left(\rho ,\; \phi \right)$. При этом полярный радиус $\rho \ge 0$, а полярный угол $0\le \phi Между полярными и декартовыми прямоугольными координатами точки $M$ можно установить связь. Для этого нужно совместить полюс и полярную ось с началом и положительным направлением оси $Ox$ прямоугольной системы координат. Из треугольника $OMM_ <1>$ получаем следующие формулы связи: Обратная тригонометрическая функция $\phi =Arctg\frac Общая формула имеет вид: \[\phi =\left\<\begin При построении графиков в полярных координатах с помощью средств MS Excel имеются некоторые особенности. График в MS Excel может быть построен, если функция однозначна и задана в декартовой прямоугольной системе координат. Для построения графика циссоиды $y^ <2>=\frac При построении графика строфоиды поступаем аналогично. Для построения графиков кардиоиды и лемнискаты такой прием не подходит, так как разрешить их уравнения в декартовой прямоугольной системе координат относительно $y$ невозможно. Поэтому рекомендуется использовать уравнения этих кривых в полярных координатах по следующей схеме: задать значение угла $\phi $ в градусах (так удобнее), перевести это значение в радианы, в соответствии с уравнением кривой вычислить значение $\rho $, вычислить декартовы координаты $x$ и $y$ по формулам $x=\rho \cdot \cos \phi $ и $y=\rho \cdot \sin \phi $. Теперь можно строить график обычным образом. http://spravochnick.ru/matematika/chislo_peremennaya_funkciya/polyarnaya_sistema_koordinat/Полярная система координат
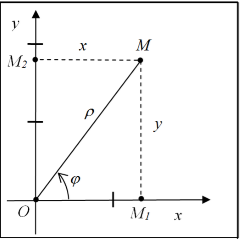
Образование полярной системы координат
Связь между прямоугольными и полярными координатами
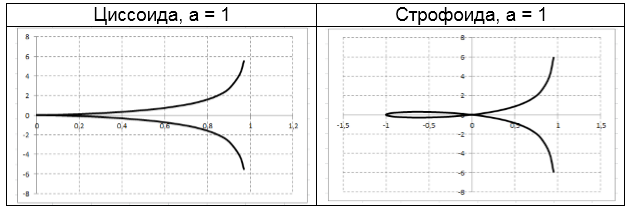
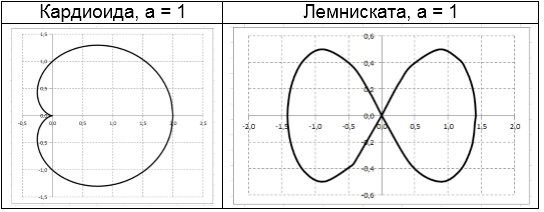
Некоторые важнейшие кривые