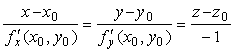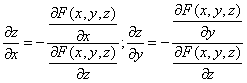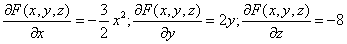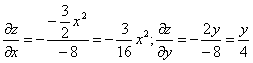Как по уравнению касательной составить уравнение плоскости

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

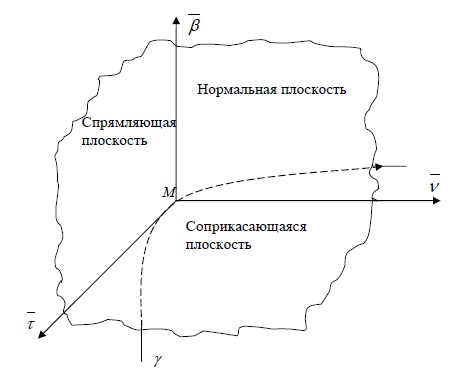
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $\gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

\begin \vec=\vec(t_0), \quad x_0=x(t_0),\, y_0=y(t_0), \, z_0=z(t_0). \end

Пусть в точке $M$ $ \vec(t_0)\neq\vec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $\vec(t_0)$.

Пусть $\vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $\lambda\in(-\infty,+\infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $\lambda$ будут соответствовать разные значения $\vec$).

Если $\vec=\$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $\gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $\vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $\vec-\vec(t_0)$ и $\vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

\begin x'(t_0)\cdot(X-x(t_0))+y'(t_0)\cdot(Y-y(t_0))+z'(t_0)\cdot(Z-z(t_0))=0. \end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ параллельно векторам $\vec(t_0)$, $\vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $\vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

\begin \left| \begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \\ x'(t_0) & y'(t_0) & z'(t_0)\\ x»(t_0) & y»(t_0) & z»(t_0) \\ \end \right|=0 \end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $\gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ \vec(t_0)\times\vec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $\vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $\vec(t_0) \times\left[\vec(t_0),\vec(t_0)\right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)\times\vec(t_0)$: \begin \left(\vec-\vec(t_0),\, \vec(t_0),\, \vec(t_0)\times\vec(t_0)\right)=0. \end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ \vec<\tau>=\frac<\vec(t_0)><|\vec(t_0)|>. $$ Орт бинормали: $$ \vec<\beta>=\frac<\vec(t_0)\times\vec(t_0)><|\vec(t_0)\times\vec(t_0)|>. $$ Орт главной нормали: $$ \vec<\nu>=\frac<\vec(t_0) \times[\vec(t_0),\,\vec(t_0)]><|\vec(t_0) \times [\vec(t_0),\,\vec(t_0)]|>. $$

Правая тройка векторов $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $\gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

\begin 1\cdot X+0\cdot Y+1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X+Z=1. \end

\begin \left| \begin X-0 & Y-0 & Z-1 \\ 1 & 0 & 1\\ 0 & 2 & 1 \\ \end \right|=0 \end Раскрываем определитель, получаем уравнение: \begin -2X-Y+2Z-2=0 \end

\begin 1\cdot X-4\cdot Y-1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X-4Y-Z+1=0. \end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ не будет правой (по определению векторного произведения вектор $\vec<\tau>\times\vec<\beta>$ направлен так, что тройка векторов $\vec<\tau>$, $\vec<\beta>$, $\vec<\nu>=\vec<\tau>\times\vec<\beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\tilde<\beta>>$ образует репер Френе для кривой $\gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,\,\, y=\frac<2>,\,\, z=\frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $\gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)\in\gamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $\vec(t_0)$, $\vec(t_0)$, поэтому записываем определитель \begin \left| \begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \\ &&\\ 1 & t_0 & t^2_0 \\ &&\\ 0 & 1 & 2t_0 \end \right|=0 \quad \Rightarrow \end

\begin (X-t_0)\cdot t_0^2 — (Y-t_0^2/2)\cdot 2t_0 + (Z-t_0^3/3)=0. \end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: \begin 9-t_0^3/3=0 \quad \Rightarrow \quad t_0=3. \end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $P\left(-\frac45,1,2\right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,\,\, y=1+t,\,\, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $\vec(t_0)$ и $\vec(t_0)\times\vec(t_0)$.

Записываем уравнение спрямляющей плоскости: \begin \left| \begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \\ 2t_0 & 1 & 2\\ 0 & 4 & -2 \end \right|= 0 \end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: \begin 5t_0^2-8t_0-4=0 \,\, \Rightarrow \,\, t_<01>=2,\, t_<02>=-\frac25. \end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: \begin & 5X-4Y-8Z+24=0,\\ & 25X+4Y+8Z=0. \end

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

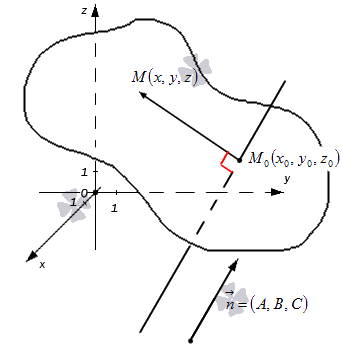
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

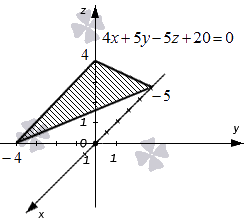
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

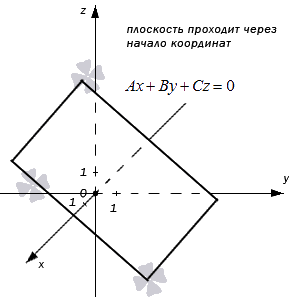
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .