Контрольная работа: Передаточные функции одноконтурной системы
| Название: Передаточные функции одноконтурной системы Раздел: Рефераты по математике Тип: контрольная работа Добавлен 21:52:15 24 декабря 2010 Похожие работы Просмотров: 508 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Y(s) |
| F(s) |
| f |
| v |
| V(s) |
| y |
| W(s) |
| ε |
| E(s) |
Рисунок 7.2. стандартная схема системы
1. Передаточная функция разомкнутой системы:



2. Передаточная функция по задающему воздействию:
Приравниваем знаменатель к нулю, получаем характеристическое уравнение замкнутой системы.

3. Передаточная функция по возмущению:
4. Передаточная функция по ошибке:
Понятие устойчивости
Очень важно изучить поведение системы во времени. В некоторых случаях процессы оказываются расходящимися, что свидетельствует о неустойчивости системы.
Для нормальной эксплуатации система должна быть устойчивой, т.е. после действия возмущения она должна возвращаться в состояние равновесия.
В качестве примера рассмотрим поведение шарика на вогнутой поверхности (желоб), выпуклой поверхности и плоской поверхности.
Устойчивая система (вогнутая поверхность), процесс сходится:
| X |
| x0 |
| t |
Неустойчивая система (выпуклая поверхность), процесс расходится:
| t |
| X |
| x0 |
Нейтральная система (горизонтальная поверхность), координата (процесс) остается постоянной.
| t |
| x0 |
| X |
Эти примеры являются механической аналогией понятия устойчивости. Рассмотрим математическое определение понятия устойчивости.
| u(t) |
| Д.У. |
| y(t) |
| U(s) |
| W(s) |
| Y(s) |
Система описывается дифференциальным уравнением:






Строго устойчивость определяется в смысле Ляпунова. Для линейных систем с постоянными параметрами считается, что система устойчива, если предел свободной составляющей равен 0

Устойчивость — внутреннее свойство системы, присущее ей вне зависимости от действующих на нее сигналов, поэтому рассматривается только свободная составляющая.
Это есть определение асимптотической устойчивости.
Свяжем требование устойчивости с расположением корней характеристического уравнения:


вещественные обозначим 
комплексные – 
Рассмотрим свободные составляющие соответствующие различным корням.
1. Корень вещественный, положительный:
| +j |
| yсв |
 |
| + |
| пл.s |
| t |
| система неустойчива |
2. Корень вещественный, отрицательный:
 +j +j |
| +j |
| пл. s |
| + |
| yсв |
| t |
| система устойчива |
3. Корни комплексные, сопряженные, с положительной вещественной частью:
| +j |
 |
 |
| yсв |
 |
| + |
| пл. s |
| t |

4. Корни комплексные, сопряженные, с отрицательной вещественной частью:
| yсв |
| +j |
 |
 |
 |
| пл. s |
| + |
| t |

Условием устойчивости является расположение корней характеристического уравнения в левой полуплоскости.
Система на границе устойчивости, если корни на мнимой оси.
Устойчивость – необходимое условие функционирования системы, поэтому в курсе уделяется много внимания методам оценки устойчивости системы.
Синтез регуляторов
Под синтезом понимается отыскание параметров вводимых в систему регуляторов, позволяющих достичь требуемые характеристики технического задания, в том числе по ограничению времени переходного процесса и показателя колебательности.
Идея синтеза линейных систем управления во временной области корневым методом состоит в том, что для структурной схемы системы, представленной, например, на рисунке, составляется характеристический полином, а также по известным требованиям к системе рассчитывается желаемый характеристический полином, после чего коэффициенты полиномов приравниваются и по полученным уравнениям составляются уравнения для определяемых параметров регуляторов.
При заданных структурах корректирующих связей и неизвестных в них параметрах осуществляется описание всей системы в виде дифференциальных уравнений, характеризующих свободное поведение системы
Тогда характеристическое уравнение примет вид:
В выражении коэффициенты a являются функциями синтезируемых параметров. Желаемое характеристическое уравнение для рассматриваемой системы имеет вид:
Все корни λi характеристического уравнения считаются известными и задаются пользователем или автоматически рассчитываются программой. Следовательно, коэффициенты bi уравнения также известны, так как рассчитываются по известным корням уравнения. Тогда уравнения представляются в виде системы уравнений:
Приравнивая полученные уравнения, будут определены значения неизвестных параметров искомой системы:
Таким образом, все неизвестные коэффициенты корректирующих звеньев могут быть получены путём решения системы уравнений. После этого полученные значения подставляются в систему, и выполняется её моделирование. Если результаты моделирования удовлетворяют требованиям, то синтез выполнен успешно. В ином случае возможно внесение изменений в требуемые характеристики системы, состоящие, например, в увеличении времени переходного процесса.
Выбор регулятора
Основным правилом при выборе порядка передаточной функции регулятора является равенство порядка всей системы и количества неизвестных параметров вводимых регуляторов. Кроме того, вводимый регулятор должен иметь как можно меньший порядок. Передаточные функции регуляторов для 0, 1 и 2 порядков имеют вид:
Так, если неизменяемая часть системы имеет 3 порядок и необходимо ввести один регулятор, то его передаточная функция может быть только W22(p), т.к. тогда порядок системы будет равен 3+2 и число неизвестных параметров (B0, B1, B2, A0, A1) также равно 5.
При выборе корней желаемого характеристического уравнения действует следующее правило. Для того, чтобы система стала устойчивой, время переходного процесса которой будет приблизительно равно tпп при колебательности μ, необходимо выбрать доминантный корень в левой полуплоскости
Значение μ выбирается исходя из технических требований. При отсутствии дополнительной информации значение показателя принимается равным 1,6. Начальное значение действительной части α0 рассчитывается следующим образом
Все последующие значения действительной части увеличиваются в 1,5–3,0 раза относительно предыдущего значения, а значение мнимой части пересчитывается согласно значению действительной части.
Пример синтеза простого объекта
На рисунке представлена структурная схема объекта с последовательным корректирующим устройством, требуется обеспечить установление всех процессов за 1 секунду. Порядок системы без введения корректора равен 1. Так как выбирается простейший корректор, порядок которого не увеличит порядок системы, а число неизвестных параметров будет равно общему порядку системы с корректором, следовательно, корректирующее устройство для рассматриваемой системы будет равно W0(p)=K.
По структурной схеме составляется матричная математическая модель системы, которая имеет вид
По матричной математической модели записываются системы дифференциальных и алгебраических уравнений
Выражая выходы звеньев и подставляя их в дифференциальное уравнение, будет получено дифференциальное уравнение и матрица A
В результате выполнения синтеза будет получено значение параметра K, которое равно 0,3.
Пример синтеза сложного объекта
Система с тремя неизвестными регуляторами представлена на рисунке. Требуется определить структуру регуляторов и найти такие их параметры, чтобы переходные процессы завершились за 0,9 секунд.
Тогда выбранные согласно правилам регуляторы представлены в структурной схеме на рисунке
Путем исключения из последующего рассмотрения внешнее воздействие и сумматор, на которое оно действует, будет получена обобщенная структура системы. Полученная система имеет пятый порядок, а число синтезируемых параметров равно 5. Так как порядок системы и число неизвестных параметров равны, то возможно применение синтеза корректирующих устройств.
Матричная математическая модель исследуемой системы имеет вид:
По матричной математической модели составляются дифференциальные уравнения:
По матричной математической модели составляются алгебраические уравнения:
После этого выражаются все сигналы y:
Тогда система дифференциальных уравнений примет вид:
Полученная система дифференциальных уравнений представляется в матричном виде:
На основе матрицы производится синтез. В результате при использовании одного из методов синтеза получены значения: K1 = 17430.482, B1 = -96867.517, A1 = 36.402, B2 = 3726.059, A2 = 2.675.
Получение характеристического уравнения в символьном виде
Для исследуемой системы, представленной на рисунке, получить характеристическое уравнение в символьном виде возможно при помощи следующего подхода.
Дифференциальные уравнения в матричном виде после подстановки zT1 и zT2 для исследуемой системы имеют вид:
В результате нахождения определителя |A-L*E| получено 2 коэффициента характеристического полинома: zT 2+ zT 1 и zT 1* zT 2+ zT 1* K 1* zT 2* K 2. Тогда, выполняя обратную подстановку для zT 1 и zT 2, получен характеристический полином в символьном виде:
Кроме того, характеристический полином может быть получен классическим способом, приравнивая знаменатель передаточной функции замкнутой системы 1+K1K2/(1+pT1)(1+pT2) к нулю.
Получение передаточных функций по структурной схеме
Для исследуемой системы, представленной на рисунке, получить передаточную функцию замкнутой системы по ошибке в символьном виде можно следующим образом.
Передаточная функция по ошибке (Y3/U) может быть вычислена путём расчёта двух матриц. Для их получения следует записать математическую модель системы без переменных состояния в подматрице алгебраических уравнений. Для динамических звеньев по главной диагонали для выходов записываются знаменатели с обратным знаком, а при входах – числители со своим знаком. Для суммирующих и усилительных звеньев по главной диагонали заносятся –1.
Тогда по условию задачи необходимо определить передаточную функцию следующего вида
Верхний определитель получен путём замены третьего столбца четвёртым, но с обратным знаком. Он отражает передаточную функцию на сумматоре Y3 при подаче воздействия U. Нижний определитель соответствует замкнутой системе. Последовательно решая определители, будет получена передаточная функция замкнутой системы по ошибке в символьном виде:
http://megaobuchalka.ru/12/9337.html
http://www.vs87.ru/d/theory/sint/
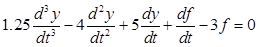 ; б)
; б)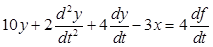 .
.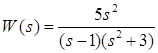 .
.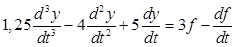 .
. .
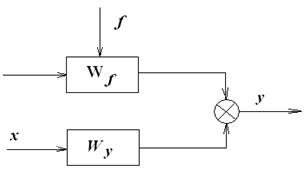
. , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.
, то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.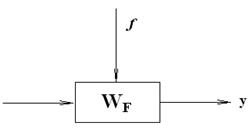
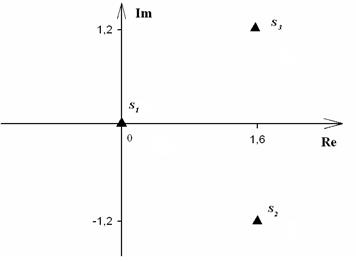
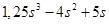 .
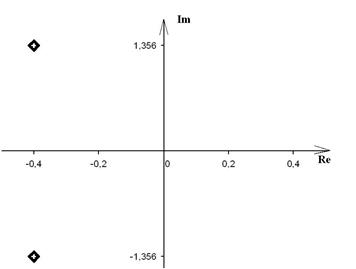
.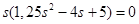 , корни которого:
, корни которого: ,
, 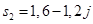 и
и 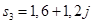 .
.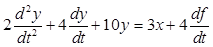 .
.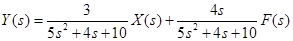 .
.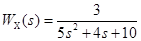 и
и  ,
,
 ,
, .
.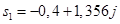 и
и 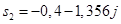 .
.
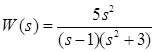
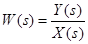 , получим:
, получим: , тогда:
, тогда: .
.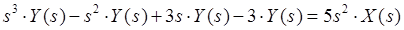
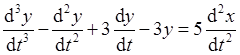 .
.
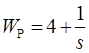 ;
;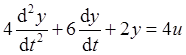 .
.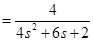 .
.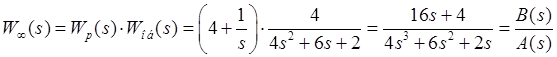
 ;
;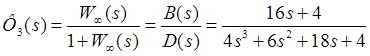 — по заданию;
— по заданию;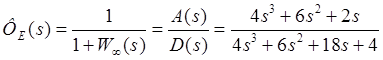 — по ошибке;
— по ошибке;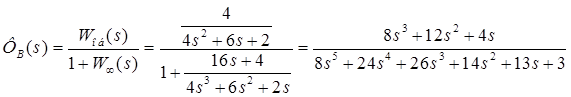 — по возмущению.
— по возмущению.