Как получить уравнение траектории пули

Движение пули в воздушной среде.

Пуля, получив при вылете из канала ствола определенную скорость, стремится по инерции сохранить величину и направление этой скорости. Если бы полет пули проходил в безвоздушном пространстве, и на нее не действовала сила тяжести, пуля двигалась бы прямолинейно, равномерно и бесконечно. Однако на пулю, летящую в воздушной среде, действуют силы, которые меняют скорость полета и направление движения. Этими силами являются сила тяжести и сила сопротивления воздушной среды.

В результате совместного действия этих двух сил пуля теряет скорость и направление своего движения, перемещаясь по кривой линии, проходящей ниже направления оси канала ствола.

Траекторией называется кривая линия, описываемая центром тяжести пули в полете.

Движение пули, а следовательно, и форма траектории зависит от многих условий. Поэтому необходимо прежде всего рассмотреть как действует на пулю сила тяжести и сила сопротивления воздуха.

Действие силы тяжести. Если представить, что на пулю, вылетевшую из канала ствола не действует никакая сила, то в таком случае она двигалась бы по инерции бесконечно, равномерно и прямолинейно по направлению оси канала ствола и за каждую секунду пролетала бы одинаковое расстояние с постоянной скоростью, равной начальной. Тогда, если бы ствол оружия был направлен прямо в цель, пуля, следуя в направлении оси канала ствола, непременно попала бы в нее. Действие сил тяжести не зависит от скорости полета снаряда. Поэтому понижение снаряда во время полета под линией бросания также будет совершаться по закону свободного падения тел и снарядов, выпущенных под каким-то углом к горизонту оружия, опишет кривую, показанную на рисунке 3.

В конце первой секунды полета под действием силы тяжести снаряд будет не в точке «а» ‘ или «а», а в точке А. Это происходит в результате поступательного движения снаряда в первоначальном направлении и движения его под действием силы тяжести. Рассматривая аналогичное положение снаряда в конце 2, 3 и т.д. секунд, мы получим точки Б, В, и т.д.

Математическим выражением закона движения снаряда является уравнение траектории, которое отражает зависимость между координатами х и у в любой точке полета снаряда. Допустим, что в безвоздушном пространстве мы произвели выстрел из орудия под углом бросания Θ₀ с начальной скоростью равной V₀ (рис. 3).

Рис. 3. Понижение снаряда под линией бросания.

Вылетев из ствола, снаряд опишет какую-то траекторию и упадет в точке Д. Необходимо найти, на какой высоте над горизонтом оружия летит снаряд на удалении X от точки вылета при данных значениях V₀ , Θ₀. Для вывода уравнения поместим начало системы координат в точке вылета, как это показано на рис. Из рисунка 4 видно, что:

Определим значения АВ и АС.

Значение АВ находится из треугольника ОА:

АС есть не что иное, как понижение снаряда под линией бросания за время его полета до точки С. Понижение как путь, проходимый свободно падающим телом, определяется по формуле:

Рис. 4. К выводу уравнения параболической траектории.

Время полета снаряда до точки С находится следующим образом:

откуда

Из треугольника ОАВ видно, что:

Подставив найденные значения АВ и АС в выражение:

,

получим уравнение траектории:

.

Полученное уравнение описывает траекторию снаряда, которая представляет параболу в безвоздушном пространстве под действием только одной силы тяжести. Траектория полета снарядов в безвоздушном пространстве представляет собой кривую, называемую параболой. Поэтому траекторию полета снарядов в пустоте называют параболической траекторией.

Для того чтобы определить, на какую дальность полетел бы снаряд в безвоздушном пространстве с данной начальной скоростью и данным углом бросания, необходимо решить уравнение траектории относительно «x». т.к. полная горизонтальная дальность есть расстояние по горизонту оружия от точки вылета до точки падения, то превышение траектории «y» в точке падения будет равно нулю. Подставляя в уравнение траекториизначение y= 0, получим:

.

Вынесем «x» за скобки:

.

Произведение может быть равно нулю в том случае, если из сомножителей: или «x», или выражение в скобке будет равно нулю. В первом случае получим х₁=0, что соответствует точке вылета. Приравнивая выражение в скобках к нулю, получим:

,

;

;

.

Используя данную формулу, мы можем определить величину начальной скорости или угол бросания, чтобы получить заданную величину полной горизонтальной дальности. Действие силы сопротивления воздуха на полет пули очень велико; оно вызывает уменьшение скорости и дальности полета пули. Например, пуля образца 1930 года при угле бросания 15° и начальной скорости 800м/сек, в безвоздушном пространстве полетела бы на дальность 32620м; дальность полета этой пули при тех же условиях, но при наличии сопротивления воздуха равна лишь 3900м.

Пуля, выброшенная из канала ствола с определенной начальной скоростью, при полете в воздухе подвергается действию двух сил: силы тяжести; силы сопротивления воздуха (рис. 5.).

Сила тяжести заставляет пулю постепенно снижаться, а сила сопротивления воздуха непрерывно замедляет движение пули и стремиться опрокинуть ее.

Сила тяжести заставляет пулю или гранату постоянно понижаться, а сила сопротивления воздуха непрерывно замедляет движение пули или гранаты стремится опрокинуть ее в результате действия этих сил скорость полета пули или гранаты постепенно уменьшается, а ее траектория представляет сбой по форме неравномерно изогнутую кривую линию.

Рис. 5. Полет пули в воздухе.

При стрельбе из огнестрельного оружия длительное время применялись круглые пули и шаровые снаряды, у которых центр тяжести (ЦТ) и центр сопротивления (ЦС) находились в одной точке, а именно, в геометрическом центре этих тел. При таком положении сила сопротивления всегда направлена в сторону, противоположную направлению полета, и действие ее сводится только к уменьшению скорости движения. Однако, ввиду плохой обтекаемости и малой поперечной нагрузки, шаровые снаряды быстро теряют свою скорость, и дальность их полета невелика. Поэтому уже с середины ХIХ века производились опытные стрельбы продолговатыми снарядами. К концу ХIХ века эта работа повсеместно закончилась введением на вооружение продолговатых пуль и снарядов. Продолговатые снаряды имеют большую поперечную нагрузку и, следовательно, большую дальность полета. Однако при такой конструкции центр тяжести не совпадает с центром сопротивления, который находится впереди ЦТ. Рассмотрим, как действует в этом случае сила сопротивления воздуха на продолговатый снаряд. Если бы сила сопротивления воздуха действовала строго вдоль оси снаряда, то ее действие на снаряд сводилось бы только к замедлению скорости полета. В действительности ее действие значительно сложнее. Уже к моменту вылета вследствие неуравновешенности и перекоса снаряда, а также вследствие давления на донную часть снаряда в период последействия газов, его ось отклоняется от направления полета, образуя с касательной к траектории угол, называемый углом нутации (δ). Это отклонение оси снаряда может произойти в любую сторону – случайно (рис. 6.). Таким образом, сила сопротивления воздуха действует не вдоль оси снаряда, а под некоторым углом к ней.

Рис. 6. Образование угла нутации.

Для выяснения действия силы сопротивления воздуха приложим к центру тяжести снаряда две взаимоуравновешивающие силы R’ и R», равные по величине силе R и противоположные по направлению (рис. 7).

Таким образом, действие силы R, приложенное в центре давления, заменяется действием R’ в центре масс и момента М пары сил R» и R’ относительно центра масс. При этом R’ — создает сопротивление в поступательном движении, а момент М стремится опрокинуть снаряд.

Сопротивление воздуха полету пули (гранаты) вызывается тем, что воздух представляет собой упругую среду (рис. 8.), и поэтому на движение в этой среде затрачивается часть энергии пули (гранаты).

Сила сопротивления воздуха вызывается тремя основными причинами:

1. Трением воздуха.

2. Образованием завихрений.

3. Образованием баллистической волны.

Рис. 7. Действие сил сопротивления воздуха

Рис. 8.Образование силы сопротивления воздуха

1. Частицы воздуха, соприкасающиеся с движущейся пулей (гранатой), вследствие внутреннего сцепления (вязкости) и сцепления с ее поверхностью создают трение и уменьшают скорость полета пули.

2. За донной частью пули образуется разряженное пространство, вследствие чего появляется разность давлений на головную и донную части. Эта разность создает силу, направленную в сторону, обратную движению пули, и уменьшает скорость ее полета. Частицы воздуха, стремясь заполнить разрежение, образовавшееся за пулей, создают завихрения.

3. Пуля (граната) при полете сталкивается с частицами воздуха и заставляет их колебаться. Вследствие этого перед пулей (гранатой) повышается плотность воздуха, и образуются звуковые волны.Поэтому полет пули (гранаты) сопровождается звуком.

При скорости полета пули (гранаты), меньшей скорости звука, образование этих волн оказывает незначительное влияние на ее полет, т.к. скорость распространения волн больше скорости полета пули (гранаты). При скорости пули, большей скорости звука, от наложения звуковых волн друг на друга создается волна сильно уплотненного воздуха – баллистическая волна, замедляющая скорость полета пули, т.к. пуля тратит часть своей энергии на создание и преодоление этой волны. Давление на фронте этой волны может достигать 8 — 10 атмосфер. Для преодоления такого большого давления у головной части расходуется наибольшая часть энергии снаряда, что приводит к резкому уменьшению скорости его полета.

Сила сопротивления воздуха зависит от:

— Величины поверхности пули;

— Скорости движения пули: при скоростях движения пули, меньших скорости звука (скорость звука при t = +15°С равна 340 м/сек.), возрастание силы сопротивления идет относительно медленно, но при переходе скорости пули свыше скорости звука наблюдается резкое увеличение сопротивления воздуха;

— Атмосферных условий: с увеличением плотности воздуха сопротивление увеличивается, причем, величина сопротивления воздуха пропорциональна его плотности.

Вследствие значительной сложности такого явления, как сопротивление воздуха, до сих пор нет полной теоретической зависимости, выражающей величину силы сопротивления. Существует ряд эмпирических формул для выражения силы сопротивления воздуха R.

Калибр снаряда (d) – площадь поперечного сечения снаряда. Приведем одну из них:

.

Сила сопротивления воздуха изменяется прямо пропорционально квадрату калибра. Это значит, что если калибр снаряда увеличить в 2 раза, то сила сопротивления воздуха увеличится в 4 раза.

В развернутом виде зависимость для оценки силы R может быть представлена в виде:

,

где: i — коэффициент формы снаряда; d — калибр снаряда; H(у) — функция, показывающая изменение плотности воздуха с высотой; F(v) — функция, показывающая зависимость изменения плотности воздуха от скорости движения.

Влияние плотности воздуха учитывается функцией Н(у), которая показывает изменение плотности воздуха с изменением высоты. Чем меньше будет плотность воздуха, тем меньше будет и сила сопротивления воздуха.

Значение Н(у) можно подсчитать по эмпирической формуле В. Ветчинкина:

,

где: у — высота полета снаряда в метрах.

Для стрелкового оружия, танковых и артиллерийских орудий при стрельбе прямой наводкой высота полета снарядов бывает очень невелика, поэтому значение Н(у) принимается равным 1.

Влияние скорости полета на величину силы сопротивления характеризуется функцией F(v), называемой функцией сопротивления.

Для приближенного определения значения F(v) можно пользоваться эмпирическими формулами.

При дозвуковых скоростях:

.

При сверхзвуковых скоростях:

.

Чем глаже поверхность пули, тем меньше сила трения и сила сопротивления воздуха. Разнообразие форм современных пуль во многом определяется необходимостью уменьшить силу сопротивления воздуха.

Баллистический коэффициент.В 1881 году, в Германии, Крупп первый собрал и упорядочил данные о влиянии сопротивления воздуха на полет и смещение пули. Крупп взял несколько тысяч пуль одинаковой формы (какой именно — не имеет значения) и замерил с большой точностью степень их замедления (потерю скорости) и снижение траектории. Такая пуля была названа «Стандартной». Было принято, что «Стандартная» пуля имеет баллистический коэффициент равный 1. Через несколько лет русский полковник Майевский разработал математическую модель для предсказания траектории пули, а затем американский полковник Ингалс опубликовал свои знаменитые таблицы, использовав формулы Майевского и данные Круппа. Их работа и сейчас, по прошествии более 100 лет, служит базой для большинства компьютерных программ по баллистике. В середине этого века пули стали более аэродинамичными и появились более совершенные способы измерения аэродинамических сил. После Второй мировой войны в США начались исследования зависимости перемещения пули от сопротивления воздуха при различной форме самой пули. Они обнаружили, что поведение пули на сверхзвуковой скорости отличается от ранее описанного. В 1965 году Винчестерн-Вестерн опубликовал баллистические таблицы для разных типов пуль и модернизированную математическую модель Ингалса/Маевского, названную «G1», а также еще одну – «G5». «G1» была принята баллистиками как лучшая и стала широко использоваться для вычисления траекторий пуль и баллистических коэффициентов. Хотя, как показали исследования, пуля не всегда летит в соответствии с этой моделью. «G5» преимущественно используется для длинных траекторий (1 000 метров и более). Для того, чтобы иметь возможность сравнивать эффективность различных пуль, предсказывать их траекторию, Ингалсом был разработан математический инструмент, который называетсябаллистический коэффициент–способность пули преодолевать сопротивление воздуха. Таким образом, баллистический коэффициент отражает соотношение сил инерции пули и сил аэродинамического сопротивления, действующих на пулю. Если какая-нибудь пуля имеет баллистический коэффициент меньше 1, то это означает, что она быстрее теряет скорость, чем «Стандартная» пуля. Для того чтобы добиться улучшения характеристик этой пули (например, скорость на дистанции 400 метров) необходимо либо увеличивать массу пули, либо улучшать ее аэродинамическую форму. До середины 20-го века считалось, что B.C. – величина постоянная (константа) для определенной пули вдоль всей траектории ее полета. Но американские баллистики выяснили, что B.C. может изменяться в зависимости от скорости. Для решения этой проблемы производители пуль применяют различные способы:

— вычисляют и указывают два или больше B.C. для изготовленной пули для разных скоростей;

— указывают приблизительный коэффициент, вычисленный из форм-фактора пули и таблиц-классификаторов. Погрешность, как правило, не более 10%;

— применяют расширенные и сложные математические модели (G1.1, G5.1, G6.1, G7.1, GS, RA4, GL, GI).

Для сверхзвуковых скоростей, когда в сопротивлении воздуха основную роль играет образование баллистической волны, наиболее выгодным является снаряд с остроконечной головной частью длиной до 3,5 калибров и донной частью с небольшой конусностью для уменьшения завихрения.

Существует формула для определения баллистического коэффициента:

,

где: W-вес пули в фунтах; d — диаметр пули в дюймах; i — форм-фактор (коэффициент формы пули или драг-коэффициент или коэффициент аэродинамического сопротивления).

Движение тела, брошенного горизонтально или под углом к горизонту.

Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.

Движение тела, брошенного горизонтально.

Выразим проекции скорости и координаты через модули векторов.

Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:

Движение тела, брошенного под углом к горизонту.

Порядок решения задачи аналогичен предыдущей.

Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):

.

Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.

Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно:

Тогда:

Максимальная высота:

Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна

Угол, под которым направлен вектор скорости в любой момент времени:

Как получить уравнение траектории пули

змбчб IV

учедеойс йъ чоеыоек вбммйуфйлй

4.2. дЧЙЦЕОЙЕ УОБТСДБ РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ

дЕКУФЧЙЕ УЙМ ФСЦЕУФЙ ОЕ ЪБЧЙУЙФ ПФ УЛПТПУФЙ РПМЈФБ УОБТСДБ. рПЬФПНХ РПОЙЦЕОЙЕ УОБТСДБ ЧП ЧТЕНС РПМЕФБ РПД МЙОЙЕК ВТПУБОЙС ФБЛЦЕ ВХДЕФ УПЧЕТЫБФШУС РП ЪБЛПОХ УЧПВПДОПЗП РБДЕОЙС ФЕМ Й УОБТСДПЧ, ЧЩРХЭЕООЩИ РПД ЛБЛЙН-ФП ХЗМПН Л ЗПТЙЪПОФХ ПТХЦЙС, ПРЙЫЕФ ЛТЙЧХА, РПЛБЪБООХА ОБ ТЙУ.24.

ч ЛПОГЕ РЕТЧПК УЕЛХОДЩ РПМЈФБ РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ УОБТСД ВХДЕФ ОЕ Ч ФПЮЛЕ «Б ‘ « ЙМЙ «Б« , Б Ч ФПЮЛЕ б .

ьФП РТПЙУИПДЙФ Ч ТЕЪХМШФБФЕ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС УОБТСДБ Ч РЕТЧПОБЮБМШОПН ОБРТБЧМЕОЙЙ Й ДЧЙЦЕОЙС ЕЗП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ.

тБУУНБФТЙЧБС БОБМПЗЙЮОПЕ РПМПЦЕОЙЕ УОБТСДБ Ч ЛПОГЕ 2, 3 Й Ф.Д. УЕЛХОД, НЩ РПМХЮЙН ФПЮЛЙ в , ч , Й Ф.Д. (ТЙУ. 24).

уПЛТБЭБС РПУМЕДПЧБФЕМШОП РТПНЕЦХФЛЙ ЧТЕНЕОЙ, ЮЕТЕЪ ЛПФПТЩЕ НЩ ПРТЕДЕМСМЙ РПМПЦЕОЙЕ УОБТСДБ, НПЦОП РПМХЮЙФШ ТСД ПЮЕОШ ВМЙЪЛП ПФУФПСЭЙИ ДТХЗ ПФ ДТХЗБ ФПЮЕЛ.

уПЕДЙОЙЧ ЬФЙ ФПЮЛЙ ЛТЙЧПК, НЩ РПМХЮЙН ЗТБЖЙЮЕУЛПЕ ЙЪПВТБЦЕОЙЕ ФТБЕЛФПТЙЙ РПМЈФБ УОБТСДБ ВЕЪ ХЮЈФБ УЙМЩ УПРТПФЙЧМЕОЙС ЧПЪДХИБ.

хТБЧОЕОЙЕ РБТБВПМЙЮЕУЛПК ФТБЕЛФПТЙЙ

нБФЕНБФЙЮЕУЛЙН ЧЩТБЦЕОЙЕН ЪБЛПОБ ДЧЙЦЕОЙС УОБТСДБ СЧМСЕФУС ХТБЧОЕОЙЕ ФТБЕЛФПТЙЙ, ЛПФПТПЕ ПФТБЦБЕФ ЪБЧЙУЙНПУФШ НЕЦДХ ЛППТДЙОБФБНЙ И Й Х Ч МАВПК ФПЮЛЕ РПМЈФБ УОБТСДБ.

чЩЧЕДЕН ХТБЧОЕОЙЕ ФТБЕЛФПТЙЙ УОБТСДБ, МЕФСЭЕЗП РПД ДЕКУФЧЙЕН ФПМШЛП ПДОПК УЙМЩ ФСЦЕУФЙ.

дПРХУФЙН, ЮФП Ч ВЕЪЧПЪДХЫОПН РТПУФТБОУФЧЕ НЩ РТПЙЪЧЕМЙ ЧЩУФТЕМ ЙЪ ПТХДЙС РПД ХЗМПН ВТПУБОЙС Θ₀ У ОБЮБМШОПК УЛПТПУФША ТБЧОПК V₀ (ТЙУ. 25).

чЩМЕФЕЧ ЙЪ УФЧПМБ, УОБТСД ПРЙЫЕФ ЛБЛХА-ФП ФТБЕЛФПТЙА Й ХРБДЈФ Ч ФПЮЛЕ д .

оЕПВИПДЙНП ОБКФЙ, ОБ ЛБЛПК ЧЩУПФЕ ОБД ЗПТЙЪПОФПН ПТХЦЙС МЕФЙФ УОБТСД ОБ ХДБМЕОЙЙ X ПФ ФПЮЛЙ ЧЩМЕФБ РТЙ ДБООЩИ ЪОБЮЕОЙСИ V₀ , Θ₀.

дМС ЧЩЧПДБ ХТБЧОЕОЙС РПНЕУФЙН ОБЮБМП УЙУФЕНЩ ЛППТДЙОБФ Ч ФПЮЛЕ ЧЩМЕФБ, ЛБЛ ЬФП РПЛБЪБОП ОБ ТЙУ. 25.

йЪ ТЙУХОЛБ ЧЙДОП, ЮФП

.

пРТЕДЕМЙН ЪОБЮЕОЙС бч Й бу .

ъОБЮЕОЙЕ бч ОБИПДЙФУС ЙЪ ФТЕХЗПМШОЙЛБ пбч ;

бу ЕУФШ ОЕ ЮФП ЙОПЕ, ЛБЛ РПОЙЦЕОЙЕ УОБТСДБ РПД МЙОЙЕК ВТПУБОЙС ЪБ ЧТЕНС ЕЗП РПМЈБ ДП ФПЮЛЙ у .

рПОЙЦЕОЙЕ ЛБЛ РХФШ, РТПИПДЙНЩК УЧПВПДОП РБДБАЭЙН ФЕМПН, ПРТЕДЕМСЕФУС РП ЖПТНХМЕ:

.

чТЕНС РПМЈФБ УОБТСДБ ДП ФПЮЛЙ у ОБИПДЙФУС УМЕДХАЭЙН ПВТБЪПН:

.

йЪ ФТЕХЗПМШОЙЛБ пбч ЧЙДОП, ЮФП

.

.

.

рПДУФБЧЙЧ ОБКДЕООЩЕ ЪОБЮЕОЙС бч Й бу Ч ЧЩТБЦЕОЙЕ

,

РПМХЮЙН ХТБЧОЕОЙЕ ФТБЕЛФПТЙЙ:

.

рПМХЮЕООПЕ ХТБЧОЕОЙЕ ПРЙУЩЧБЕФ ФТБЕЛФПТЙА УОБТСДБ, ЛПФПТБС РТЕДУФБЧМСЕФ РБТБВПМХ Ч ВЕЪЧПЪДХЫОПН РТПУФТБОУФЧЕ РПД ДЕКУФЧЙЕН ФПМШЛП ПДОПК УЙМЩ ФСЦЕУФЙ.

фТБЕЛФПТЙС РПМЈФБ УОБТСДПЧ Ч ВЕЪЧПЪДХЫОПН РТПУФТБОУФЧЕ РТЕДУФБЧМСЕФ УПВПК ЛТЙЧХА, ОБЪЩЧБЕНХА РБТБВПМПК .

рПЬФПНХ ФТБЕЛФПТЙА РПМЈФБ УОБТСДПЧ Ч РХУФПФЕ ОБЪЩЧБАФ РБТБВПМЙЮЕУЛПК ФТБЕЛФПТЙЕК.

рБТБВПМЙЮЕУЛЙЕ ФТБЕЛФПТЙЙ ЙНЕАФ УМЕДХАЭЙЕ УЧПКУФЧБ:

• ФТБЕЛФПТЙС РТЕДУФБЧМСЕФ УПВПК РМПУЛХА УЙННЕФТЙЮОХА ЛТЙЧХА ПФОПУЙФЕМШОП ЧЕТЫЙОЩ, Ф.Е. ЧЕТЫЙОБ ФТБЕЛФПТЙЙ ОБИПДЙФУС РПУТЕДЙОЕ РПМОПК ЗПТЙЪПОФБМШОПК ДБМШОПУФЙ;

ЧПУИПДСЭБС ЧЕФЧШ ФТБЕЛФПТЙЙ ТБЧОБ ОЙУИПДСЭЕК ЧЕФЧЙ;

ЧТЕНС РПМЈФБ УОБТСДБ ПФ ФПЮЛЙ ЧЩМЕФБ ДП ЧЕТЫЙОЩ ТБЧОП ЧТЕНЕОЙ РПМЈФБ ПФ ЧЕТЫЙОЩ ДП ФПЮЛЙ РБДЕОЙС;

ХЗПМ РБДЕОЙС РП УЧПЕК БВУПМАФОПК ЧЕМЙЮЙОЕ ТБЧЕО ХЗМХ ВТПУБОЙС;

ПЛПОЮБФЕМШОБС УЛПТПУФШ УОБТСДБ ТБЧОБ ОБЮБМШОПК УЛПТПУФЙ;

рТЙ УФТЕМШВЕ Ч ЧПЪДХИЕ УОБТСДБНЙ У ОЕВПМШЫЙНЙ ОБЮБМШОЩНЙ УЛПТПУФСНЙ ЙИ ФТБЕЛФПТЙЙ ВМЙЪЛЙ Л РБТБВПМЙЮЕУЛЙН.

рПЬФПНХ, ЛБЛ ХЛБЪЩЧБМПУШ Ч ПЮЕТЛЕ РП ЙУФПТЙЙ ВБММЙУФЙЛЙ, ДПМЗПЕ ЧТЕНС ЧУЕ ТБУЮЈФЩ ДМС УФТЕМШВЩ ЧЕМЙУШ РП ЧЩЧЕДЕООПНХ ХТБЧОЕОЙА РБТБВПМЙЮЕУЛПК ФТБЕЛФПТЙЙ.

Движение тела, брошенного горизонтально или под углом к горизонту.
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты. Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
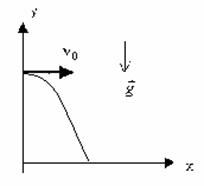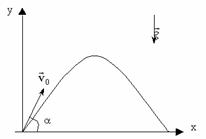
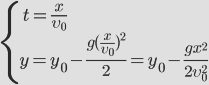	— между координатами квадратичная зависимость, траектория – парабола!
Следовательно, для решения этой задачи необходимо решить уравнение
Оно будет иметь решение при t=0 (начало движения) и
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.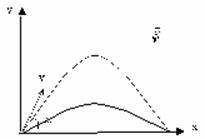
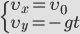
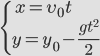
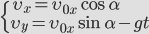
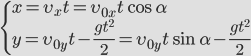
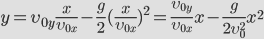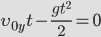
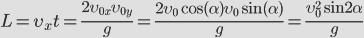
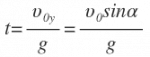
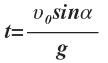
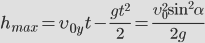
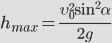
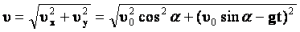