Как понять производная положительная или отрицательная по уравнению

Производная

Производная – отношение приращения функции к приращению ее аргумента при приращении аргумента стремящемся.

ЭЙ-ЭЙ, СТОЙТЕ. Куда вы побежали-то? Сейчас легко и просто всё объясню! Приготовьтесь, текста будет много. Зато понятно и наглядно. Так же в конце будут разобраны примеры из ЕГЭ.

Понятие производной на интервале

Пусть у нас есть некоторая линейная функция , определенная на промежутке \([a;b]\). Что значит слово «определенная»? Это значит, что для любого \(x\) из этого промежутка значений мы можем найти соответствующий \(y\) (смотрите, например, следующий график).

Возьмем на этом промежутке \([a;b]\) некоторое значение аргумента — \(x_A\). Ему соответствует точка \(A\) на графике и значение функции \(y_A\).

Теперь дадим выбранному значению \(x_A\) некоторое приращение \(∆x\). Эта запись — \(∆x\) — читается как «дельта икс» и означает величину изменения икса.
То есть мы увеличиваем значение \(x_A\) на \(∆x\). Тогда мы сдвинемся по оси \(x\) и попадем в некое \(x_B\) равное \(x_A+∆x\).
Очевидно, что «расстояние» между \(x_B\) и \(x_A\) равно как раз \(∆x\) (см. график), то есть приращению аргумента. И это приращение аргумента есть «длина» интервала, который мы рассматриваем.

Значению аргумента \(x_B\) соответствует точка \(B\) на графике и значение функции \(y_B\).
Давайте обозначим «расстояние» между \(y_B\) и \(y_A\) как некоторое \(∆y\) (аналогично тому, как это было сделано на оси \(x\)).
Что такое \(∆y\)? Подумайте – был аргумент равный \(x_A\), ему соответствовало значение функции \(y_A\). Потом мы аргумент увеличили на \(∆x\) (до \(x_B\)), при этом значение функции тоже выросло до \(y_B\). Что такое тогда \(∆y\) равное разности между \(y_B\) и \(y_A\)? Верно, это приращение значения функции при соответствующем приращении аргумента!

Так вот — если мы теперь разделим \(∆y\) на \(∆x\), то получим производную функции на интервале \(∆x\) (от \(x_A\) до \(x_B\)). В этом суть понятия «производная» на интервале – это просто число, которое получится, если поделить длину отрезка ∆y на длину соответствующего ему отрезка \(∆x\).

Производная на интервале — это отношение приращения функции на интервале к ширине этого интервала (то есть приращению аргумента).

Внимание! Это определение не математически строгое, а «по смыслу», для понимания.

То есть, производная на интервале показывает насколько сильно изменилась функция по отношению к некоторому изменению аргумента этой функции. Или по-другому: производная на интервале характеризует скорость роста функции на этом интервале.

Действительно, посмотрите два графика ниже.

На первом графике при росте аргумента с \(3\) до \(4\), функция выросла с \(1\) до \(4\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<3><1>=3\)

На втором графике при росте аргумента с \(3\) до \(4\), функция выросла с \(2\) до \(3\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<1><1>=1.\)

Легко заметить, что график слева «круче», а график справа – более «пологий», т.е. \(f(x)\) растет быстрее, чем \(g(x)\). И производная слева – больше, чем справа. Это логично, ведь фактически производная – это дробь \(\frac<∆y><∆x>\), а если числитель дроби увеличить, то и значение всей дроби тоже растет.

Производная на интервале характеризует скорость роста функции. Чем больше производная – тем быстрее растет функция на интервале.

Хорошо, теперь вопрос на засыпку тем, кто читал внимательно. А что будет с производной, если график линейной функции падает?
Давайте рассмотрим эту ситуацию.

Функция \(f(x)\) падает, то есть при росте аргумента, значение функции становиться все меньше.
Действительно, при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит, \(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\).
Тогда значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<-3><1>=-3\).

То есть, если функция на интервале падает – производная станет отрицательна.
Причем, чем круче падает функция, тем больше по модулю будет значение производной. Посмотрите на графики ниже, и вы в этом сами убедитесь.

На первом графике при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<-3><1>=-3\).

На втором графике при росте аргумента с \(2\) до \(3\), функция упала с \(2\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-2=-1\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<-1><1>=-1\).

Если функция падает – производная на интервале отрицательна.

Осталось рассмотреть последнюю ситуацию — а если функция в точке не возрастает и не убывает? Что будет с производной в этом случае? Смотрите график ниже.

Вот, например, функция, имеющая прямолинейный участок, параллельный оси \(x\) на интервале \((2;4)\). Понятно, что если мы рассмотрим этот интервал, то изменение функции \(∆y\) на нем равно нулю, ведь на нем функция не растет и не падает и для любой точки равна \(2\).
И тогда производная равна \(\frac<∆y><∆x>=\frac<0><∆x>=0\).

Если функция не растет и не падает – производная на интервале равна \(0\).

Понятие производной в точке

Хорошо, мы разобрали производную на интервале для линейной функции. А если функция отличается от прямой?

Первый порыв ответить: «да какая разница, делаем также!» — неверен. Дело в том, что на прямой была не важна длина рассматриваемого интервала, ведь для неё значение производной – постоянная величина на любом интервале. Смотрите на график ниже:

Если мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(3\). То есть, \(∆x=4-2=2\), \(∆y=3-1=2\), т.е. значение производной на интервале \((2;4)\) равно \(\frac<∆y><∆x>=\frac<2><2>=1\).

Если мы рассмотрим интервал по иксу с \(2\) до \(3\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=3-2=1\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<1><1>=1\).

И на любом другом интервале будет тоже самое — и на \((2;5)\), и на \((3;4)\), и на \((3;5)\) – производная везде равна \(1\). Это и логично, ведь скорость роста функции везде одинакова.

Теперь давайте посмотрим график некоторой нелинейной функции.

Если мы рассмотрим интервал по иксу с \(2\) до \(5\), то на нем прирост значения функции – с \(1\) до \(4\). То есть, \(∆x=5-2=3\), \(∆y=4-1=3\), т.е. значение производной на интервале \((2;5)\) равно \(\frac<∆y><∆x>=\frac<3><3>=1\).

Если же мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=4-2=2\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;4)\) равно \(\frac<∆y><∆x>=\frac<1><2>=0,5\).

Получается, что значение производной изменяется в зависимости от ширины рассматриваемого интервала. Чтобы выйти из этой ситуации и при этом сохранить все вышеописанную логику, математики придумали следующую хитрость.

Дело в том, что при увеличении масштаба график любой нелинейной функции становится все больше похож на линейный.

Вот, например, график параболы \(y=x^2\), построенный на компьютере с высокой точностью, на интервале от \(-5\) до \(5\). Видно, что график ну очень далек от прямой.

А если рассмотреть тот же график, но на более узком интервале?

Вот тот же график, но уже на интервале от \(0\) до \(2\). Видно, что он изрядно «распрямился».

А вот он же на интервале от \(1\) до \(1,1\). Визуально он уже мало отличается от прямой, хотя на самом деле очень небольшое искривление все же есть. Понятно, что если сжимать интервал еще сильнее, то вскоре график будет практически неотличим от прямой.

Таким образом, вся вышеописанная логика вполне применима и для нелинейных графиков, но только на очень маленьких интервалах. А что мы получим, если будем БЕСКОНЕЧНО уменьшать ширину интервал? Мы будем сжимать его до точки. А что такое «ширина интервала»? Это ни что иное как \(∆x\)! Значит, чтобы найти производную в точке, мы должны посмотреть приращение функции на бесконечно малом (или, говоря более научно, стремящемся к нулю) приращении аргумента. Именно так в математике и вводится понятие производной в точке:

Производная в точке – есть отношение приращения функции к соответствующему приращению ее аргумента при приращении аргумента, стремящемся к нулю.

Таким образом, вся описанная выше логика дифференцирования линейных функций, применима для бесконечно малых участков функций нелинейных. Значит, и все сделанные ранее выводы будут верны. Например, если нелинейная функция в точке (точнее, на бесконечно малом интервале в окрестности этой точки) возрастает, то производная в точке будет положительна. А если функция в точке убывает — производная будет отрицательна.

Остается вопрос – а есть ли на нелинейных функциях точки, где производная равна нулю? Ответ – да, в точках экстремумов. Помните, что это за точки такие?

Экстремумы – это точки максимумов и минимумов функции.

Напомню, что максимумом функции называется самая «высокая» точка на некотором интервале, а минимумом, соответственно, самая «низкая».

Вот, например, функция \(y=(x-5)^2 (x+1)-15\).Она имеет максимум при \(x=1\) и минимум при \(x=5\).
И в этих точках функция действительно не растет и не падает.
Давайте посмотрим на большем масштабе, чтобы в этом убедится.

Вот окрестность точки максимума \(x=1\) с очень маленьким шагом.

А это окрестность точки минимума \(x=5\) с очень маленьким шагом.

Думаю, комментарии излишни. Вообще говоря, чтобы понять, что в максимумах и минимумах функция «останавливается» достаточно просто внимательно об этом подумать.

Вдумайтесь, как образуется, допустим, максимум? Функция растет, растет, но после какой-то точки начинает падать. Значит, функция меняет «направление движения» на противоположное. Но это невозможно сделать без остановки! Попробуйте бежать в одну сторону, а потом взять и резко побежать в обратную (не просто повернуть, а именно в противоположную сторону). Вы в любом случае остановитесь при смене направления хоть на долю секунды. Также и функции. С минимумом — аналогично.

Таким образом, получается, что в окрестности точек минимума и максимума функция идет параллельно оси \(x\). И в них производная равна нулю. Слово «в окрестности», употребленное выше, означает «очень-очень близко возле точки». Например, промежуток \((1,99999; 2,00001)\) можно назвать окрестностью точки со значением \(2\).

— Чем больше значение производной функции в точке – тем быстрее в этой точке растет функция.
— Если производная в точке положительна, функция в этой точке растет, если производная в точке отрицательна, функция в ней падает.
— В точках максимумов и минимумов функции – производная равно \(0\).

Эти принципы стоит запомнить (а еще лучше просто понять), потому что с их помощью можно решать огромное количество задач на производные, в том числе и из ЕГЭ.

Пример (ЕГЭ). На рисунке изображен график функции, определенной на интервале \((-3;7)\). Определите количество целых точек, в которых производная данной функции отрицательна.

Решение: Начинаем анализировать. Где производная будет отрицательна? Там, где функция падает, то есть от точки А до точки В и от точки С до точки D.

При этом в задаче просят найти количество ЦЕЛЫХ точек. А что такое «целая точка»? Это такая точка графика, у которой икс целое число (например, \(-5\), \(0\) или \(17\), но не \(3,25\) или \(0,7\)).

То есть нам нужны именно такие точки на участках АВ и CD графика. Всего их четыре (обозначены на графике красным ромбом). Обратите внимание, что точка С в ответ не входит, так как это точка максимума и в ней производная равно \(0\), а ноль неотрицателен.

Пример (ЕГЭ). На рисунке изображен график функции \(y=f(x)\) и отмечены точки \(−2\), \(1\), \(3\) и \(9\). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Решение: Давайте думать.
В точке с координатой \(-2\) функция убывает (падает), значит производная будет отрицательна (ведь она показывает, как раз изменение функции).
В точке с координатой \(1\) – функция медленно растет, значит производная будет, во-первых, положительна, а во-вторых, мала по значению (ведь рост медленный).
В точке с координатой \(3\) – максимум, значит функция не растет и не падает, следовательно, производная будет равна нулю.
И наконец, в точке \(9\) – функция растет и быстро (по крайней мере, быстрее, чем в точке \(1\)). Значит здесь производная положительна и велика.
Таким образом, с учетом всех предыдущих рассуждений, делаем вывод: наибольшее значение производной будет в точке \(9\).

Довольно часто в практике попадаются обратные задачи – когда дан график производной, а анализировать надо график функции. Вот, например, такая задача из ЕГЭ:

Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) -производной для функции \(y(x)\). Найдите количество точек экстремумов функции \(y(x)\) на изображенном интервале.

Решение: Экстремумы – это точки минимумов и максимумов функции. Но у нас дан график производной, а не функции. А что происходит с производной в тех точках, где на функции минимум или максимум?
Верно, в этих точках производная равна нулю. Значит, нам нужны все точки, где значение производной ноль! Это точки А, B, C, D и Е. Всего их \(5\), это и есть ответ задачи.

Пример (ЕГЭ). На рисунке изображен график \(y'(x)\) — производной для функции \(y(x)\) определенной на интервале \((−7; 7)\). Найдите промежутки возрастания функции \(y(x)\). В ответе укажите длину наибольшего из них.

Решение: Мы знаем, что если функция возрастает – производная положительна, а если падает – то отрицательна. Однако верно и обратное:
— если производная положительна – функция растет,
— если производная отрицательна – функция падает.
Исходя из этого становиться очевидно, что исходная функция \(y(x)\) возрастает на участках \((-5;-2)\) и \((1;6)\) – они выделены зеленым. И длина наибольшего из них равна \(5\).

Производная функции. Геометрический смысл производной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку A с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

Величина в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси . Значит, в точке производная положительна.

В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».

В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

Ты нашел то, что искал? Поделись с друзьями!

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.

О производных

Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я «предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения. Казалось бы, и что статья с таким началом может делать в этом блоге?

А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.

Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.

Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
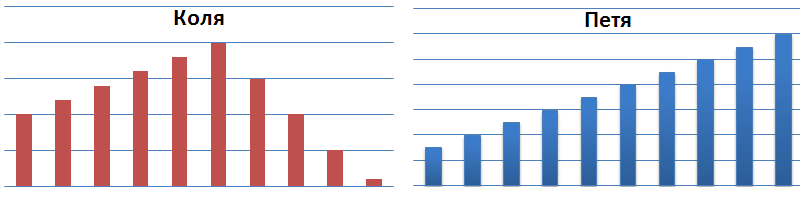
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.

Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.

Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
И, конечно же, опять — нифига подобного!

Глянем вот на этот график:

Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.

К чему это я?

1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:

• А где работаешь?
• А кем?
• Сколько получаешь?

и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.

2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.

3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?