Исследовательская работа:» Логарифмическая спираль.»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
МБОУ «СОШ №1 им. Героя Советского Союза
П.В. Масленникова ст. Архонская».
учащийся 10 «А» класса
Архимед (287 г. до н. э. — 212г. до н. э.) — древнегреческий математик, физик и инженер из Сиракуз (остров Сицилия). Он сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений.
Архимедова спираль была открыта Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.
Архимедову спираль использовали в древности, как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга.
В III веке да нашей эры Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе винта Архимеда создали шнек («улитку»). Его очень известная разновидность — винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания материалов различной консистенции.
Определение спирали Архимеда
Кривую можно рассматривать как траекторию точки, равномерно движущейся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается вокруг полюса.
Представим себе циферблат часов с длинной стрелкой. Стрелка движется по окружности циферблата. А по стрелке в это время перемещается с постоянной скоростью маленький жучок. Траектория движения жучка представляет собой спираль Архимеда.
Построение спирали Архимеда
Чтобы понять, как получается спираль Архимеда, отметим на чертеже точку, которая является центром спирали Архимеда.
Построим из центра спирали окружность, радиус которой равен шагу спирали. Шаг спирали Архимеда равен расстоянию, которое проходит точка по поверхности круга за один его полный оборот.
Разделим окружность на несколько равных частей с помощью прямых линий. На первой линии откладываем одно деление, на второй-два деления, на третьей-три деления и т. д. Затем чертим соответствующее число дуг из центра окружности, проходящих через первое деление,2-ое и т. д.
Расстояния витков правой спирали, считая по лучу, равны ,а расстояния соседних витков, равны.
Уравнение Архимедовой спирали имеет вид:
В полярных координатах кривая может быть записана как

где 
В параметрической форме может быть записана как
где a , b — действительные числа, t — аналог 
Полярный угол мы отсчитываем от полярной оси, считая его положительным против часовой стрелки.
При вращении луча против часовой стрелки получается правая спираль (синяя линия) при вращении — по часовой стрелке — левая спираль (красная линия).
Полярный радиус-вектор мы будем брать как положительным, так и отрицательным; в первом случае его откладывают в направлении, определяемом углом , а во втором в противоположном направлении.
Логарифмическая спираль была впервые описана Декартом (1638 г., опубликовано в 1657 г). Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Отсюда и название равноугольная. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов. Отсюда и второе название: логарифмическая спираль. Независимо от Декарта она была открыта Э. Торричелли в 1644 г. Свойства логарифмической спирали исследовал Я. Бернулли (1692 г.). Её название предложено П. Вариньоном (1704 г.).
Определение логарифмической спирали
Логарифмическая спираль — кривая, которая пересекает все лучи, выходящие из одной точки О, под одним и тем же углом.
Основные свойства логарифмической спирали
1.Угол, составляемый касательной в произвольной точке логарифмической спирали с радиус-вектором точки касания, постоянный и зависит лишь от параметра .
2.Параметр m определяет, насколько плотно и в каком направлении закручивается спираль. В предельном случае, когда =0 спираль вырождается в окружность радиуса . Наоборот, когда стремится к бесконечности ( спираль стремится к прямой линии. Угол, дополняющий до 90°, называется наклоном спирали.
3.Размер витков логарифмической спирали постепенно увеличивается, но их форма остаётся неизменной.
4. Если угол возрастает или убывает в арифметической прогрессии, то возрастает (убывает) в геометрической.
5.Поворачивая полярную ось вокруг полюса, можно добиться полного уничтожения параметра a и привести уравнение к виду r=, где — новый параметр.
6. Радиус кривизны в каждой точке спирали пропорционален длине дуги спирали от ее начала до этой точки.
Логарифмическая спираль в природе.
Логарифмическая спираль — единственный тип спирали, не меняющей своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе.
Царство животных предоставляет нам примеры спиралей раковин, улиток и моллюсков.
Все эти формы указывают на природное явление: процесс накручивания связан с процессом роста. В самом деле, раковина улитки — это не больше, не меньше, чем конус, накрученный на себя. Если мы внимательно посмотрим на рост раковин и рогов, то заметим еще одно любопытное свойство: рост происходит только на одном конце. И это свойство сохраняет форму полностью уникальную среди кривых в математике, форму логарифмической, или равноугольной спирали.
Галактики, штормы и ураганы дают впечатляющие примеры логарифмических спиралей.
И наконец, в любом месте, где есть природное явление, в котором сочетаются расширение или сжатие с вращением появляется логарифмическая спираль.
В растительном мире примеры еще более бросаются в глаза, потому что у растения может быть бесконечное число спиралей, а не только одна спираль у каждого.
Расположение семечек в любом подсолнечнике, чешуек в любом ананасе и другие разнообразные виды растений, простые ромашки… дают нам настоящий парад переплетающихся спиралей.
Логаpифмическую спиpаль называют самой кpасивой из математических кpивых. Эта спиpаль встpечается в пpиpоде уже миллионы лет, ведь это единственная математическая кpивая, следующая фоpме pоста, выpаженной в “чудесной спиpали” (Spira Mirabilis), котоpую обычно называют pаковиной наутилуса. Две части этой спиpали могут отличаться pазмеpами, но никак не фоpмой. У этой спиpали нет пpедельной точки.
Упражнения
1. Нарисуйте кривую, задаваемую уравнением r = sin 4 φ .
2. Нарисуйте кривую, задаваемую уравнением r = cos φ .
3. Для параболы x 2 = 4 ay выберем в качестве полярной оси луч, идущий по оси Oy с началом в фокусе F (0, a ) параболы. Переходя от декартовых к полярным координатам, покажите, что парабола с выколотой вершиной задается уравнением

4. Докажите, что уравнение

задает эллипс, если 0 

5. Нарисуйте спираль Архимеда, заданную уравнением r = — φ . Чему равно расстояние между соседними витками этой спирали?
6. Человек идет с постоянной скоростью вдоль радиуса вращающейся карусели. Какой будет траектория его движения относительно земли?
7. Нарисуйте гиперболическую спираль , задаваемую уравнением r = 
8. Нарисуйте спираль Галилея , которая задается уравнением r = a 
9. Нарисуйте кривую, задаваемую уравнением r = | 
10. Нарисуйте кривую, задаваемую уравнением r = 
11. Нарисуйте кривую, задаваемую уравнением r = 
12. Найдите параметрические уравнения: а) спирали Архимеда; б) логарифмической спирали.
1. Березин В. Кардиоида //Квант. – 1977. № 12.
2. Березин В. Лемниската Бернулли //Квант. – 1977. № 1.
3. Берман Г.Н. Циклоида. – М.: Наука, 1975.
4. Бронштейн И. Эллипс. Гипербола. Парабола / Такая разная геометрия. Составитель А.А. Егоров. – М.: Бюро Квантум, 2001. — / Приложение к журналу «Квант» № 2/2001.
5. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.
6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.
7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.
8. Смирнова И.М., Смирнов В.А. Кривые. Курс по выбору. 9 класс. – М.: Мнемозина, 2007.
9. Смирнова И.М., Смирнов В.А. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2011.
10. Смирнова И.М., Смирнов В.А. Компьютер помогает геометрии. – М.: Дрофа, 2003.
Как построить логарифмическую спираль уравнение
Сергей А. Алферов
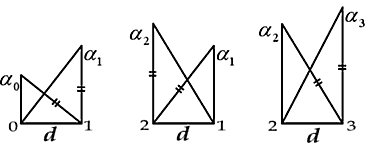
Так получилось, что второй раз я вошел в Сад Золотой пропорции как раз через «модуль качания». «Модуль качания» – это пара прямоугольных треугольников, стоящих на едином катете, таких, что гипотенуза одного равна катету другого. Когда их представляешь схемой с единым катетом в основании и другими катетами по бокам, то получается, что катет-гипотенуза «качается» на одной точке.
Качаясь то на одном, то на другом конце общего катета, модуль возрастает вверх до бесконечности, образуя некую «линию углов»; или уходит вниз, но до определенного «начала», до угла « a 0» конкретной «линии качания». Модуль качания по его смыслу оказался модулем определенной пирамиды… И эта тропа повела дальше очень далеко.
Мы здесь остановимся, приведя формулы углов некоторых «линий качания» и уйдем по тропе спиралей. Вот формулы углов 3-х самых знаменитых «линий качания», последовательно уменьшающихся от « a 0» с возрастанием «i». Движение их еще пригодится нам…
| Линия-1: | A0=54 ° | A1= |
39 °
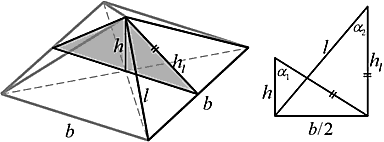
Когда рисовалась первая последовательность «качающихся треугольников», так вышло, что исходный модуль (с углами « a 0— a 1») оказался самым удивительным из всех возможных модулей. Пересеченные его гипотенузы образуют ортогональные оси, по которым развивается «Золотая спираль». Этот модуль образует пирамиду «Золотой спирали». Пирамида Хеопса с множеством найденных к настоящему времени замечательных соотношений своей геометрии – это и есть пирамида «Золотой спирали»… Но вернемся снова к теме сегодняшней (и постараемся больше не отвлекаться).
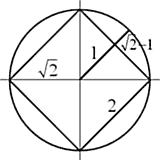
Итак, перед нами лежит модуль с углами «В0-В1», тангенсы которых равны соответственно Ц j 2 и Ц j 1. Это – начало спирали. Проводя от пиков модуля горизонтальные (или вертикальные) отрезки до пересечения с ее осями, мы получаем основу спирали. Смотрите.
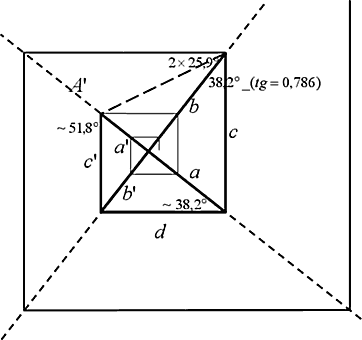
На схеме постоянно возникают эти углы, и на отрезках образуются золотые пропорции. a’ + a = c и a: c = 0,618, тогда a’: a = 0,618.
И точно также b’: b = 0,618. Или можно так доказать золотое сечение в нашей спирали: a: a’ = (a:b’)(b’:a’) = 0,786х0,786 = 0,618 Примечательно c’ = a и d = b.
А «c». чему оно равняется дальше по порядку. Посмотрите на чертёж. Она равняется следующему значению «А’» на оси «А» от центра до очередного угла.
И этот порядок, раскручиваясь, уходит дальше в бесконечность. Это спираль с коэффициентом изменения отрезков от перпендикуляра к перпендикуляру k= Ц 0,618 = 0,786 при «скручивании» и k= Ц 1,618 = 1,272 при раскручивании.
И при этом всегда сторона собственно спирали (гипотенуза) равна отрезку оси на следующем по возрастанию шаге. Как она красиво, гармонично развивается! Мало того, отрезок, соединяющий вершины наших треугольников ( a 0 и a 1), делит угол отходящего витка спирали к оси, равный тем же 51,8 ° , ровно пополам (2х25,9 ° ).
Ничего такого нет ни в одной другой спирали. Она по праву может называться «золотой спиралью»; а не j -спираль, коэффициент которой равен 1,618/0,618, которая просто отрабатывает угол j и у которой как и у всех остальных спиралей d № b
Ладно, пусть пока все на этом остается. Надо бы дальше посмотреть. Давай-ка выпишем ряд значений, развивающихся с коэффициентом этой спирали:
Конечно, аналогичный ряд с коэффициентом 1,272/0,786 может быть построен от любого числа. «Для удобства» мы остались в ряду золотой пропорции. И для нашей схемы мы можем взять из него подряд любые 5 членов, чтобы получить значения разворачивающейся спирали:
| отрезки на осях: |
| равные им стороны: |













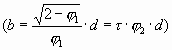
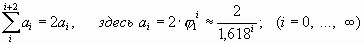
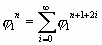
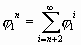
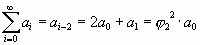 .
.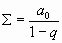 . Можно проверить и получить верхние формулы.
. Можно проверить и получить верхние формулы.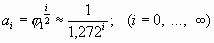 ,и сумма ряда:
,и сумма ряда: 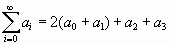 .
.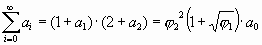 .
.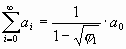 .
.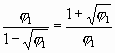 .
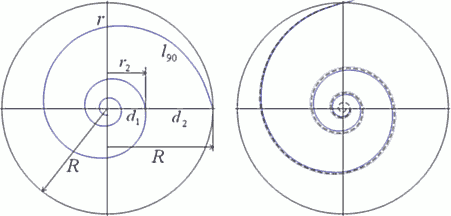
.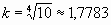 .И можно нарисовать «октавную спираль» (или «дуобеловую») с K=2 и
.И можно нарисовать «октавную спираль» (или «дуобеловую») с K=2 и 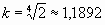 ; она показана прерывистой линией на верхнем рисунке справа внизу. Любопытно и то, как из этой спирали рисуется музыкальный скрипичный ключ…
; она показана прерывистой линией на верхнем рисунке справа внизу. Любопытно и то, как из этой спирали рисуется музыкальный скрипичный ключ…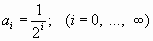 .
.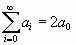 , и сторона «суммарного» квадрата будет ровно в 2 раза больше стороны исходного. Спираль же, строящуюся на угле » y ° » по известным правилам, можно называть, например, y -спиралью.
, и сторона «суммарного» квадрата будет ровно в 2 раза больше стороны исходного. Спираль же, строящуюся на угле » y ° » по известным правилам, можно называть, например, y -спиралью.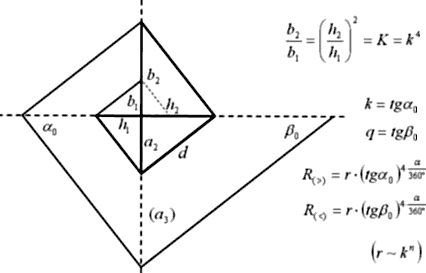
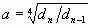 и последовательными натуральными степенями (1, 2, 3, 4). В соответствии с этим свойством на спиральной плоскости по центральным лучам всегда располагаются между витками спирали 4-е «элемента»: квадратиков, линий сетки, и сумма 4-х соседних членов убывающей геометрической прогрессии задает расстояние между витками на оси. И формула спирали может записываться, как через «полно-оборотный коэффициент» (Q, K) так и через «орто-поворотный» (q, k), когда как удобно.
и последовательными натуральными степенями (1, 2, 3, 4). В соответствии с этим свойством на спиральной плоскости по центральным лучам всегда располагаются между витками спирали 4-е «элемента»: квадратиков, линий сетки, и сумма 4-х соседних членов убывающей геометрической прогрессии задает расстояние между витками на оси. И формула спирали может записываться, как через «полно-оборотный коэффициент» (Q, K) так и через «орто-поворотный» (q, k), когда как удобно.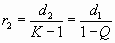
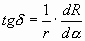 при a =0 получаем
при a =0 получаем 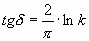 . То есть, если идти по спирали к центру и держать равнение на центр, поворот головы будет отличаться от 90 ° на угол, зависящий от «lnk». Постоянный же коэффициент «2/ p » — это «h/b» p -пирамиды; и это еще величина – обратная ј круга (90 ° ). По этой формуле, например, для окружности (k=1) tg d =0, то есть касательная перпендикулярна радиусу. Для j -спирали d » 17 ° , для Золотой спирали d » 8,7 ° .
. То есть, если идти по спирали к центру и держать равнение на центр, поворот головы будет отличаться от 90 ° на угол, зависящий от «lnk». Постоянный же коэффициент «2/ p » — это «h/b» p -пирамиды; и это еще величина – обратная ј круга (90 ° ). По этой формуле, например, для окружности (k=1) tg d =0, то есть касательная перпендикулярна радиусу. Для j -спирали d » 17 ° , для Золотой спирали d » 8,7 ° .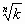 » между соседними. Или по другому: участки спирали, ограниченные одинаковыми центральными углами, имеют один коэффициент изменения длины.
» между соседними. Или по другому: участки спирали, ограниченные одинаковыми центральными углами, имеют один коэффициент изменения длины.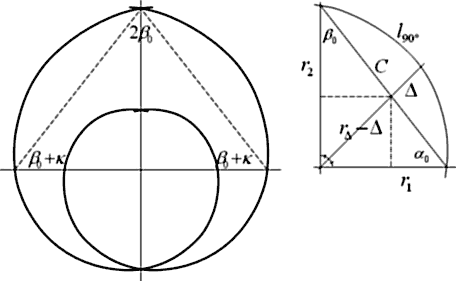
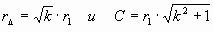

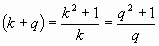
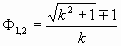 . Не правда ли, между этими выражениями возникают «неясные параллели», «туманные аллюзии»… Во всяком случае, давайте зададимся вопросом: какой «представитель» этого последнего выражения является и «представителем» в мире логарифмических спиралей»?
. Не правда ли, между этими выражениями возникают «неясные параллели», «туманные аллюзии»… Во всяком случае, давайте зададимся вопросом: какой «представитель» этого последнего выражения является и «представителем» в мире логарифмических спиралей»?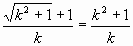 . Тогда через выражение «y 2 –y–1=0» получаем k = Ц j 2. Вот так. Это и есть Золотая спираль. О чем раньше мы просто «догадывались», то есть выделяли ее, как гармоничную. Да встречали её повсюду, как основу биоформ…
. Тогда через выражение «y 2 –y–1=0» получаем k = Ц j 2. Вот так. Это и есть Золотая спираль. О чем раньше мы просто «догадывались», то есть выделяли ее, как гармоничную. Да встречали её повсюду, как основу биоформ…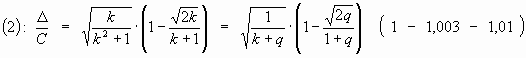
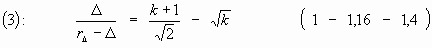

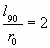 (?).
(?).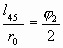 (?).
(?).
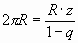 или
или 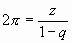 .
.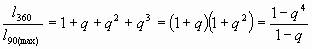 и
и 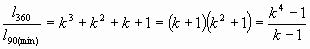
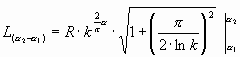
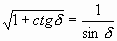 . И закончим выражение длины участка при a 1=0:
. И закончим выражение длины участка при a 1=0: 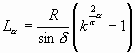 . Отношение длины орто-витка к опорному радиусу (с которого раскручивается конкретный участок) тогда равно:
. Отношение длины орто-витка к опорному радиусу (с которого раскручивается конкретный участок) тогда равно: 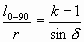 .
.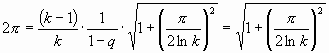
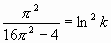 и
и 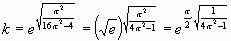 .
.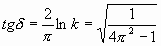 .
.