Как построить пару пересекающихся прямых по каноническому уравнению

Исследование уравнений второго порядка

Преобразование координат в уравнении второго порядка.

В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ <2>+ 2Bxy + Cy^ <2>+ 2Dx + 2Ey + F = 0,\label
$$
в котором коэффициенты \(A\), \(B\) и \(C\) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения \eqref не изменится.

При повороте базиса декартовой прямоугольной системы координат на угол \(\varphi\) старые координаты точки \(x\), \(y\) будут связаны с ее новыми координатами \(x’\), \(y’\) формулами
$$
x = x’\cos \varphi-y’\sin \varphi,\\ y = x’\sin \varphi + y’\cos \varphi.\nonumber
$$
В новых координатах уравнение \eqref примет вид
$$
A(x’\cos \varphi-y’\sin \varphi)^ <2>+ 2B(x’\cos \varphi-y’\sin \varphi) \times \\ \times (x’\sin \varphi + y’\cos \varphi) + C(x’\sin \varphi + y’\cos \varphi) + … = 0.\nonumber
$$
Здесь многоточием обозначены члены первой степени относительно \(x’\), \(y’\) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением \(x’y’\) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при \(x’y’\) есть
$$
B’ = -A\sin \varphi \cos \varphi + B(\cos^<2>\varphi-\sin^<2>\varphi) + C\sin \varphi \cos \varphi.\nonumber
$$
Если \(B = 0\), то поворачивать систему координат не будем. Если же \(B \neq 0\), то выберем угол \(\varphi\) так, чтобы \(B’\) обратилось в нуль.

Это требование приведет к уравнению
$$
2B \cos 2\varphi = (A-C)\sin 2\varphi.\label
$$
Если \(A = C\), то \(\cos 2\varphi = 0\), и можно положить \(\varphi = \pi/4\). Если же \(A \neq C\), то выбираем \(\varphi = \displaystyle\frac<1> <2>\operatorname \left[\frac<2B>\right]\). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ <\ 2>+ C’y’^ <\ 2>+ 2D’x’ + 2E’y’ + F’ = 0.\label
$$
Выражения для коэффициентов уравнения \eqref через коэффициенты \eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.

Если в уравнение \eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.

В самом деле, пусть, например, \(A’ \neq 0\). Перепишем \eqref в виде
$$
A’\left(x’^ <\ 2>+ \frac<2D’>x’ + \frac>>\right) + C’y’^ <\ 2>+ 2E’y’ + F’-\frac = 0.\nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами \(x″ = x’ + D’/A’\), \(y″ = y’\), то уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ 2E’y″ + F″ = 0,\nonumber
$$
как и требовалось.

Канонические виды уравнений второго порядка.

Предположим, что \(A’C’ \neq 0\), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ <\ 2>+ C’y″^ <\ 2>+ F″ = 0.\label
$$

Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.

Случай A’C’ > 0.

Если \(A’C’ > 0\), то коэффициенты \(A’\) и \(C’\) имеют один знак. Для \(F″\) имеются следующие три возможности.

Знак \(F″\) противоположен знаку \(A’\) и \(C’\). Перенесем \(F″\) в другую часть равенства и разделим на него. Уравнение примет вид
$$
\frac>> + \frac>> = 1,\label
$$
где \(a^ <2>= -F″/A’\), \(b^ <2>= -F″/C’\). Можно считать, что в этом уравнении \(a > 0\), \(b > 0\) и \(a \geq b\). Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат
$$
x^ <*>= y″,\ y^ <*>= x″.\label
$$

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(a \geq b\), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.

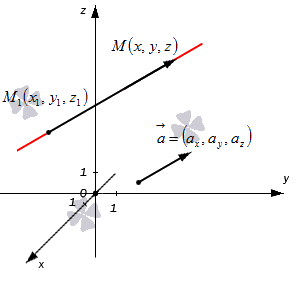
При \(a = b\) уравнение \eqref есть уравнение окружности радиуса \(a\). Таким образом, окружность — частный случай эллипса.

Случай A’C’ Определение.

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.

Случай \(A’C’ = 0\).

Допустим теперь, что \(A’C’ = 0\), и, следовательно, один из коэффициентов \(A’\) или \(C’\) равен нулю. В случае необходимости, делая замену \eqref, мы можем считать, что \(A’ = 0\). При этом \(C \neq 0\), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ <\ 2>+ 2D’x″ + F″ = 0.\nonumber
$$

Пусть \(D’ \neq 0\). Сгруппируем члены следующим образом:
$$
C’y″^ <\ 2>+ 2D’\left(x″ + \frac<2D’>\right) = 0.\nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода \(x^ <*>= x″ + F″/2D’\), \(y^ <*>= y″\). Тогда уравнение примет вид
$$
C″y^ <*2>+ 2D’x^ <*>= 0,\nonumber
$$
или
$$
y^ <*2>= 2px^<*>,\label
$$
где \(p = -D’/C″\). Мы можем считать, что \(p > 0\), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: \(\tilde = -x^<*>\), \(\tilde = y^<*>\).

Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением \eqref при условии \(p > 0\), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.

Допустим, что \(D’ = 0\). Уравнение имеет вид \(C’y″^ <\ 2>+ F″ = 0\). Относительно \(F″\) есть следующие три возможности.

1. Если \(C’F″ 0\) знаки \(C’\) и \(F″\) совпадают. Разделив на \(C’\), приведем уравнение к виду
   $$
   y″^ <\ 2>+ a^ <2>= 0.\label
   $$
   Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду \eqref, называют уравнением пары мнимых параллельных прямых.
2. Остался последний случай \(F″ = 0\). После деления на \(C’\) уравнение принимает вид
   $$
   y″^ <\ 2>= 0.\label
   $$
   Это уравнение эквивалентно уравнению \(y″ = 0\), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду \eqref, называется уравнением пары совпавших прямых.

Теперь мы можем объединить всё вместе.

Пусть в декартовой системе координат задано уравнение второго порядка \eqref.

Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:

1. Уравнение эллипса.
   $$
   \frac>> + \frac>> = 1;\nonumber
   $$
2. Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
   $$
   \frac>> + \frac>> = -1;\nonumber
   $$
3. Уравнение пары мнимых пересекающихся прямых (точка).
   $$
   a^<2>x^ <2>+ c^<2>y^ <2>= 0;\nonumber
   $$
4. Уравнение гиперболы.
   $$
   \frac>>-\frac>> = 1;\nonumber
   $$
5. Пересекающиеся прямые.
   $$
   a^<2>x^<2>-c^<2>y^ <2>= 0;\nonumber
   $$
6. Уравнение параболы.
   $$
   y^ <2>= 2px;\nonumber
   $$
7. Пара параллельных прямых.
   $$
   y^<2>-a^ <2>= 0;\nonumber
   $$
8. Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
   $$
   y^ <2>+ a^ <2>= 0;\nonumber
   $$
9. Прямая (пара совпавших прямых).
   $$
   y^ <2>= 0.\nonumber
   $$

Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,

Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:

M 1 M → = x — x 1 , y — y 1 , z — z 1

После этого нужное нам условие мы можем сформулировать так: M 1 M → = x — x 1 , y — y 1 , z — z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.

При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Между правыми частями после этого можно будет поставить знак равенства:

x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

В итоге у нас получились уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.

Если один-два параметра a равны 0 , то уравнение x — x 1 a x = y — y 1 a y = z — z 1 a z носит условный характер. Его следует считать равным следующей записи:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:

x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 2 a x = y — y 2 a y = z — z 2 a z .

2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 1 μ · a x = y — y 1 μ · a y = z — z 1 μ · a z .

Вот несколько примеров таких уравнений с заданными значениями:

x — 3 2 = y + 1 — 1 2 = z ln 7

Тут x 1 = 3 , y 1 = — 1 , z 1 = 0 , a x = 2 , a y = — 1 2 , a z = ln 7 .

x — 4 0 = y + 2 1 = z + 1 0

Тут M 1 ( 4 , — 2 , — 1 ) , a → = ( 0 , 1 , 0 ) .

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z — 3 — 5 . Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , — 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , — 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).

Ответ: 4 · μ , 2 · μ , — 5 · μ , μ ∈ R , μ ≠ 0

Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , — 3 , 2 ) и имеет направляющий вектор с координатами — 1 , 0 , 5 .

Решение

У нас есть данные, что x 1 = 0 , y 1 = — 3 , z 1 = 2 , a x = — 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 0 — 1 = y — ( — 3 ) 0 = z — 2 5 ⇔ ⇔ x — 1 = y + 3 0 = z — 2 5

Ответ: x — 1 = y + 3 0 = z — 2 5

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x — x 1 a x = y — y 1 a y = z — z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:

В первом случае:
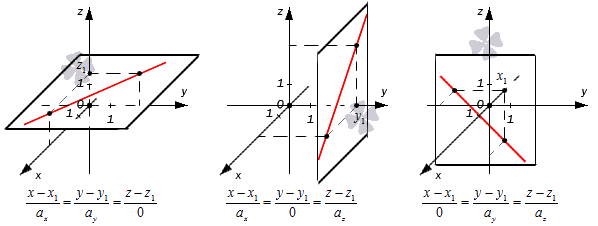
x — x 1 0 = y — y 1 a y = z — z 1 a z = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x — x 1 = 0 y — y 1 a y = z — z 1 a z = λ

Во втором случае:
x — x 1 a x = y — y 1 0 = z — z 1 a z = λ ⇔ x = x 1 + a x · λ y — y 1 = 0 z = z 1 + a z · λ ⇔ y — y 1 = 0 x — x 1 a x = z — z 1 a z = λ

В третьем случае:
x — x 1 a x = y — y 1 a y = z — z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z — z 1 = 0 ⇔ z — z 1 = 0 x — x 1 a x = y — y 1 a y = λ

Получается, что при таком значении параметров нужные прямые находятся в плоскостях x — x 1 = 0 , y — y 1 = 0 или z — z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.

Следовательно, мы сможем записать канонические уравнения немного иначе.

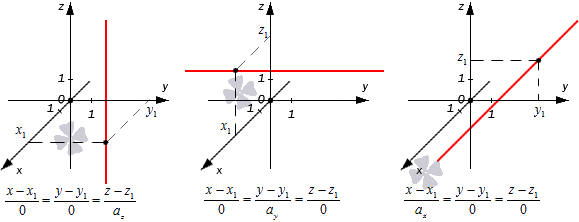
1. В первом случае: x — x 1 0 = y — y 1 0 = z — z 1 a z = λ ⇔ x — x 1 = 0 y — y 1 = 0 z = z 1 + a z · λ , λ ∈ R
2. Во втором: x — x 1 0 = y — y 1 a y = z — z 1 0 = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ , λ ∈ R z — z 1 = 0
3. В третьем: x — x 1 a x = y — y 1 0 = z — z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z — z 1 = 0

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Покажем на примерах, как применяются эти правила.

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .

Решение

Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой O x : x 1 = y 0 = z 0

Для прямой O y : x 0 = y 1 = z 0

Для прямой O z : x 0 = y 0 = z 1

Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .

В пространстве задана прямая, которая проходит через точку M 1 ( 3 , — 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

x — 3 0 = y — ( — 1 ) 1 = z — 12 0 ⇔ x — 3 0 = y + 1 1 = z — 12 0

Ответ: x — 3 0 = y + 1 1 = z — 12 0

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M 1 M 2 → = x 2 — x 1 , y 2 — y 1 , z 2 — z 1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

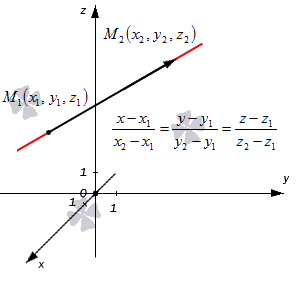
x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

в пространстве есть две точки с координатами M 1 ( — 2 , 4 , 1 ) и M 2 ( — 3 , 2 , — 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, x 1 = — 2 , y 1 = — 4 , z 1 = 1 , x 2 = — 3 , y 2 = 2 , z 2 = — 5 . Нам требуется подставить эти значения в каноническое уравнение:

x — ( — 2 ) — 3 — ( — 2 ) = y — ( — 4 ) 2 — ( — 4 ) = z — 1 — 5 — 1 ⇔ x + 2 — 1 = y + 4 6 = z — 1 — 6

Если мы возьмем уравнения вида x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , то у нас получится: x — ( — 3 ) — 3 — ( — 2 ) = y — 2 2 — ( — 4 ) = z — ( — 5 ) — 5 — 1 ⇔ x + 3 — 1 = y — 2 6 = z + 5 — 6

Ответ: x + 3 — 1 = y — 2 6 = z + 5 — 6 либо x + 3 — 1 = y — 2 6 = z + 5 — 6 .

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x — x 1 a x = y — y 1 a y = z — z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ z — z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x — 2 3 = y — 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к λ .

x — 2 3 = y — 2 = z + 7 0 ⇔ x — 2 3 = λ y — 2 = λ z + 7 0 = λ

Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:

x — 2 3 = λ y — 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7 + 0 · λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7

Ответ: x = 2 + 3 · λ y = — 2 · λ z = — 7

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x — x 1 a x = y — y 1 a y = z — z 1 a z нужно для начала представить в виде системы уравнений:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a x y — y 1 a y = z — z 1 a z

Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a z y — y 1 a y = z — z 1 a z ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) a z · ( x — x 1 ) = a x · ( z — z 1 ) a z · ( y — y 1 ) = a y · ( z — z 1 ) ⇔ ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

В итоге у нас вышло, что:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y — a x 0 a z 0 — a x 0 a z — a y = 0 и один из определителей второго порядка не равен 0 :

a y — a x a z 0 = a x · a z , a y 0 a z — a x = a x · a y , — a x 0 0 — a x = a x 2 a y — a x 0 a z = a y · a z , a y 0 0 — a y = — a y 2 , — a x 0 a z — a y = a x · a y a z 0 0 a z = a z 2 , a z — a x 0 — a y = — a y · a z , 0 — a x a z — a y = a x · a z

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Прямая задана каноническим уравнением x — 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

x — 1 2 = y 0 = z + 2 0 ⇔ x — 1 2 = y 0 x — 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x — 1 ) = 2 y 0 · ( x — 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x — 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x — 1 2 = y 0 = z + 2 0

Ответ: y = 0 z + 2 = 0

Прямая задана уравнениями x + 1 2 = y — 2 1 = z — 5 — 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

x + 1 2 = y — 2 1 = z — 5 — 3 ⇔ x + 1 2 = y — 2 1 x + 1 2 = z — 5 — 3 y — 2 1 = z — 5 — 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y — 2 ) — 3 · ( x + 1 ) = 2 · ( z — 5 ) — 3 · ( y — 2 ) = 1 · ( z — 5 ) ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + 7 — 11 = 0

Получаем, что определитель основной матрицы полученной системы будет равен 0 :

1 — 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( — 2 ) · 2 · 0 + 0 · 3 · 3 — 0 · 0 · 0 — 1 · 2 · 3 — ( — 2 ) · 3 · 1 = 0

Минор второго порядка нулевым при этом не будет: 1 — 2 3 0 = 1 · 0 — ( — 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:

x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Ответ: x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.