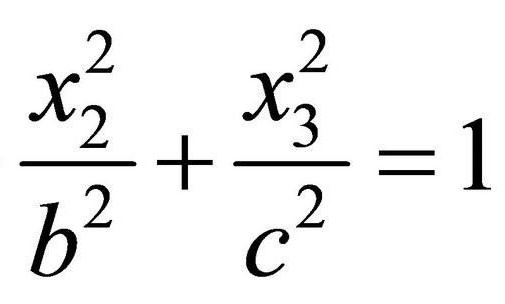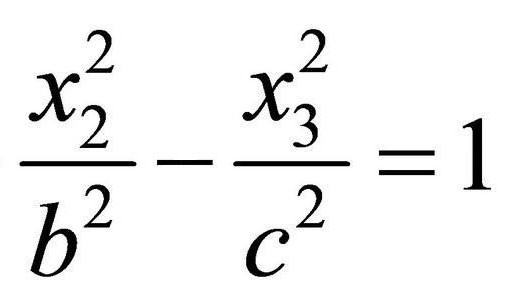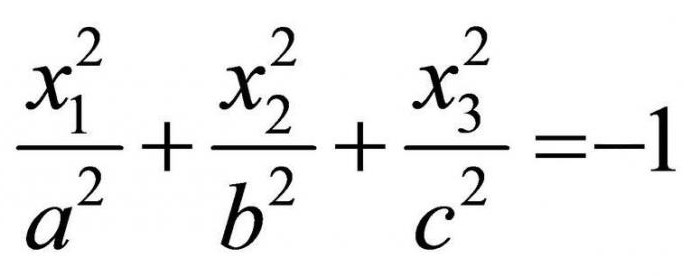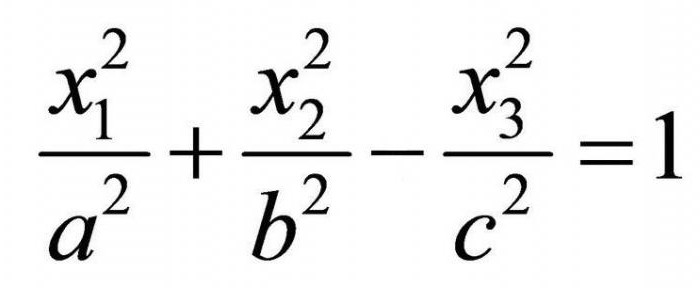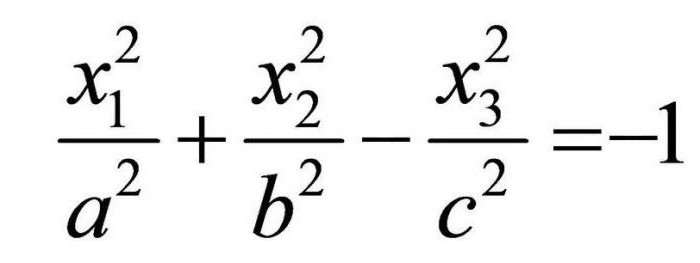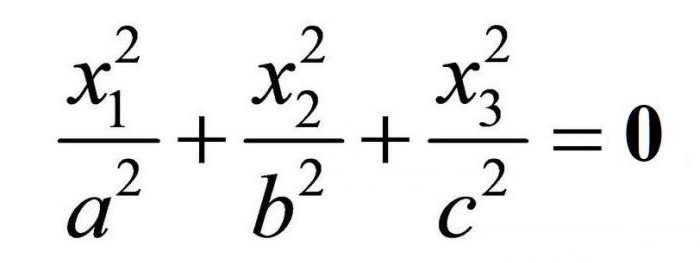Как построить поверхность второго порядка по уравнению

Поверхности 2 порядка: примеры

С поверхностями 2-го порядка студент чаще всего встречается на первом курсе. Сначала задачи на эту тему могут казаться простыми, но, по мере изучения высшей математики и углубления в научную сторону, можно окончательно перестать ориентироваться в происходящем. Для того чтобы такого не произошло, надо не просто заучить, а понять, как получается та или иная поверхность, как изменение коэффициентов влияет на нее и ее расположение относительно изначальной системы координат и как найти новую систему (такую, в которой ее центр совпадает с началом координат, а ось симметрии параллельна одной из координатных осей). Начнем с самого начала.

Определение

Поверхностью 2 порядка называется ГМТ, координаты которого удовлетворяют общему уравнению следующего вида:

Ясно, что каждая точка, принадлежащая поверхности, должна иметь три координаты в каком-либо обозначенном базисе. Хотя в некоторых случаях геометрическое место точек может вырождаться, например, в плоскость. Это лишь значит, что одна из координат постоянна и равна нулю во всей области допустимых значений.

Полная расписанная форма упомянутого выше равенства выглядит так:

A_nm – некоторые константы, x, y, z – переменные, отвечающие аффинным координатам какой-либо точки. При этом хотя бы один из множителей-констант должен быть не равен нулю, то есть не любая точка будет отвечать уравнению.

В подавляющем большинстве примеров многие числовые множители все же тождественно равняются нулю, и уравнение значительно упрощается. На практике определение принадлежности точки к поверхности не затруднено (достаточно подставить ее координаты в уравнение и проверить, соблюдается ли тождество). Ключевым моментом в такой работе является приведение последней к каноническому виду.

Написанное выше уравнение задает любые (все указанные далее) поверхности 2 порядка. Примеры рассмотрим далее.

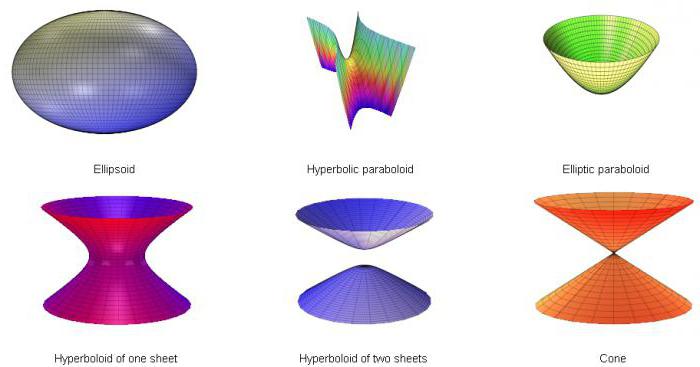
Виды поверхностей 2 порядка

Уравнения поверхностей 2 порядка различаются только значениями коэффициентов A_nm. Из общего вида при определенных значениях констант могут получиться различные поверхности, классифицируемые следующим образом:

Цилиндры.
Эллиптический тип.
Гиперболический тип.
Конический тип.
Параболический тип.
Плоскости.

У каждого из перечисленных видов есть естественная и мнимая форма: в мнимой форме геометрическое место вещественных точек либо вырождается в более простую фигуру, либо отсутствует вовсе.

Цилиндры

Это самый простой тип, так как относительно сложная кривая лежит только в основании, выступая в качестве направляющей. Образующими являются прямые, перпендикулярные плоскости, в которой лежит основание.

На графике показан круговой цилиндр – частный случай эллиптического цилиндра. В плоскости XY его проекция будет эллипсом (в нашем случае — кругом) — направляющей, а в XZ – прямоугольником – так как образующие параллельны оси Z. Чтобы получить его из общего уравнения, необходимо придать коэффициентам следующие значения:

Вместо привычных обозначений икс, игрек, зет использованы иксы с порядковым номером – это не имеет никакого значения.

По сути, 1/a 2 и другие указанные здесь постоянные являются теми самыми коэффициентами, указанными в общем уравнении, но принято записывать их именно в таком виде – это и есть каноническое представление. Далее будет использоваться исключительно такая запись.

Так задается гиперболический цилиндр. Схема та же – направляющей будет гипербола.

Параболический цилиндр задается несколько иначе: его канонический вид включает в себя коэффициент p, называемый параметром. На самом деле, коэффициент равен q=2p, но принято разделять его на представленные два множителя.

Есть еще один вид цилиндров: мнимые. Такому цилиндру не принадлежит ни одна вещественная точка. Его описывает уравнение эллиптического цилиндра, но вместо единицы стоит -1.

Эллиптический тип

Эллипсоид может быть растянут вдоль одной из осей (вдоль которой именно зависит от значений постоянных a, b, c, указанных выше; очевидно, что большей оси будет соответствовать больший коэффициент).

Также существует и мнимый эллипсоид – при условии, что сумма координат, помноженная на коэффициенты, равна -1:

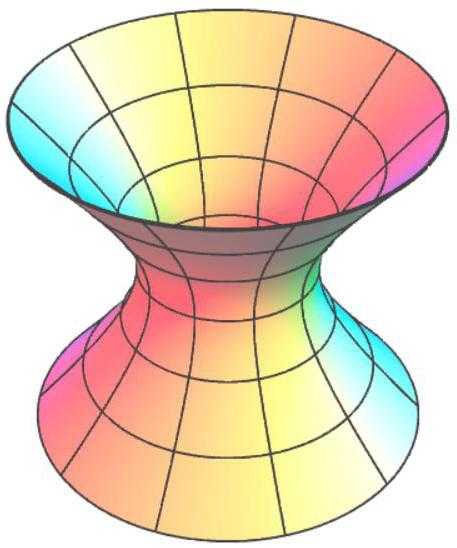
Гиперболоиды

При появлении минуса в одной из констант уравнение эллипсоида превращается в уравнение однополостного гиперболоида. Надо понимать, что этот минус не обязательно должен располагаться перед координатой x₃! Он лишь определяет, какая из осей будет осью вращения гиперболоида (или параллельна ей, так как при появлении дополнительных слагаемых в квадрате (например, (x-2) 2 ) смещается центр фигуры, как следствие, поверхность перемещается параллельно осям координат). Это относится ко всем поверхностям 2 порядка.

Кроме этого, надо понимать, что уравнения представлены в каноническом виде и они могут быть изменены с помощью варьирования констант (с сохранением знака!); при этом их вид (гиперболоид, конус и так далее) останется тем же.

Такое уравнение задает уже двуполостный гиперболоид.

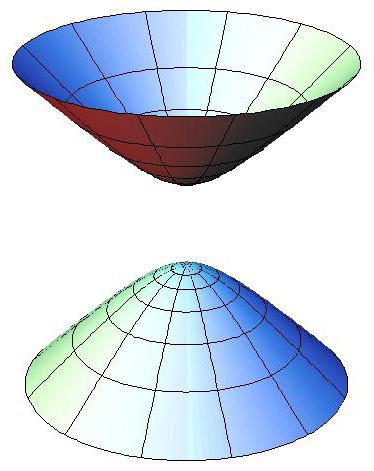
Коническая поверхность

В уравнении конуса единица отсутствует – равенство нулю.

Конусом называется только ограниченная коническая поверхность. На картинке ниже видно, что, по сути, на графике окажется два так называемых конуса.

Важное замечание: во всех рассматриваемых канонических уравнениях константы по умолчанию принимаются положительными. В ином случае знак может повлиять на итоговый график.

Координатные плоскости становятся плоскостями симметрии конуса, центр симметрии располагается в начале координат.

В уравнении мнимого конуса стоят только плюсы; ему принадлежит одна единственная вещественная точка.

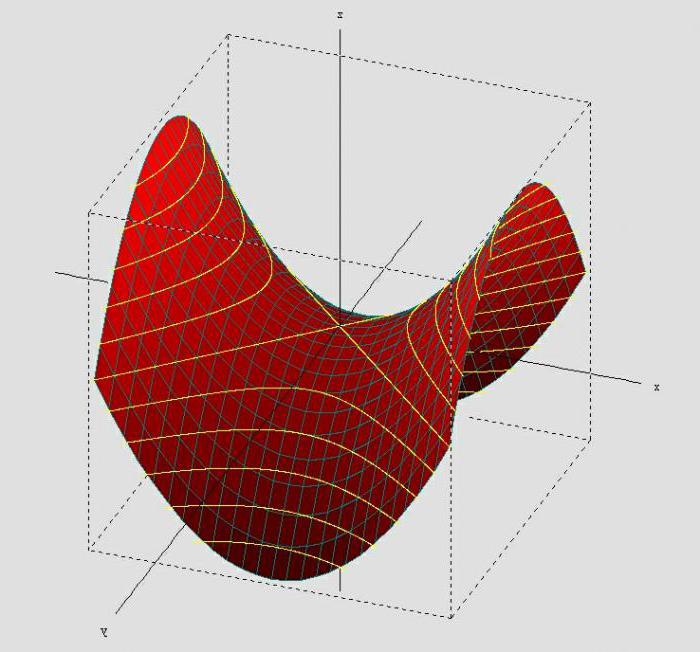
Параболоиды

Поверхности 2 порядка в пространстве могут принимать различные формы даже при схожих уравнениях. К примеру, параболоиды бывают двух видов.

x 2 /a 2 +y 2 /b 2 =2z

Эллиптический параболоид, при расположении оси Z перпендикулярно чертежу, будет проецироваться в эллипс.

x 2 /a 2 -y 2 /b 2 =2z

Гиперболический параболоид: в сечениях плоскостями, параллельными ZY, будут получаться параболы, а в сечениях плоскостями, параллельными XY – гиперболы.

Пересекающиеся плоскости

Есть случаи, когда поверхности 2-ого порядка вырождаются в плоскости. Эти плоскости могут располагаться различными способами.

Сначала рассмотрим пересекающиеся плоскости:

x 2 /a 2 -y 2 /b 2 =0

При такой модификации канонического уравнения получаются просто две пересекающиеся плоскости (мнимые!); все вещественные точки находятся на оси той координаты, которая отсутствует в уравнении (в каноническом – оси Z).

Параллельные плоскости

При наличии только одной координаты поверхности 2-го порядка вырождаются в пару параллельных плоскостей. Не забывайте, на месте игрека может стоять любая другая переменная; тогда будут получаться плоскости, параллельные другим осям.

В этом случае они становятся мнимыми.

Совпадающие плоскости

При таком простом уравнении пара плоскостей вырождается в одну – они совпадают.

Не забывайте, что в случае трехмерного базиса представленное выше уравнение не задает прямую y=0! В нем отсутствуют две другие переменные, но это всего лишь значит, что их значение постоянно и равно нулю.

Построение

Одной из самых сложных задач для студента является именно построение поверхностей 2 порядка. Еще более затруднительно переходить от одной системы координат к другой, учитывая углы наклона кривой относительно осей и смещение центра. Давайте повторим, как последовательно определить будущий вид чертежа аналитическим способом.

Чтобы построить поверхность 2 порядка, необходимо:

привести уравнение к каноническому виду;
определить вид исследуемой поверхности;
построить, опираясь на значения коэффициентов.

Ниже представлены все рассмотренные виды:

Для закрепления подробно распишем один пример такого типа задания.

Примеры

Допустим, имеется уравнение:

3(x 2 -2x+1)+6y 2 +2z 2 +60y+144=0

Приведем его к каноническому виду. Выделим полные квадраты, то есть скомпонуем имеющиеся слагаемые таким образом, чтобы они были разложением квадрата суммы или разности. Например: если (a+1) 2 =a 2 +2a+1, то a 2 +2a+1=(a+1) 2 . Мы будем проводить вторую операцию. Скобки в данном случае раскрывать не обязательно, так как это только усложнит вычисления, а вот вынести общий множитель 6 (в скобке с полным квадратом игрека) необходимо:

3(x-1) 2 +6(y+5) 2 +2z 2 =6

Переменная зэт встречается в этом случае только один раз – ее можно пока не трогать.

Анализируем уравнение на данном этапе: перед всеми неизвестными стоит знак «плюс»; при делении на шесть остается единица. Следовательно, перед нами уравнение, задающее эллипсоид.

Заметьте, что 144 было разложено на 150-6, после чего -6 перенесли вправо. Почему надо было сделать именно так? Очевидно, что самый большой делитель в данном примере -6, следовательно, чтобы после деления на него справа осталась единица, необходимо «отложить» от 144 именно 6 (о том, что справа должна оказаться единица, говорит наличие свободного члена – константы, не помноженной на неизвестную).

Поделим все на шесть и получим каноническое уравнение эллипсоида:

(x-1) 2 /2+(y+5) 2 /1+z 2 /3=1

В использованной ранее классификации поверхностей 2 порядка рассматривается частный случай, когда центр фигуры находится в начале координат. В данном примере он смещен.

Полагаем, что каждая скобка с неизвестными – это новая переменная. То есть: a=x-1, b=y+5, c=z. В новых координатах центр эллипсоида совпадает с точкой (0,0,0), следовательно, a=b=c=0, откуда: x=1, y=-5, z=0. В изначальных координатах центр фигуры лежит в точке (1,-5,0).

Эллипсоид будет получаться из двух эллипсов: первого в плоскости XY и второго в плоскости XZ (или YZ – это не имеет значения). Коэффициенты, на которые делятся переменные, стоят в каноническом уравнении в квадрате. Следовательно, в приведенном примере правильнее было бы делить на корень из двух, единицу и корень из трех.

Меньшая ось первого эллипса, параллельная оси Y, равняется двум. Большая ось, параллельная оси X – двум корням из двух. Меньшая ось второго эллипса, параллельная оси Y, остается той же – она равна двум. А большая ось, параллельная оси Z, равняется двум корням из трех.

С помощью полученных из первоначального уравнения путем преобразования к каноническому виду данных мы можем начертить эллипсоид.

Подводя итоги

Освещенная в этой статье тема довольно обширная, но, на самом деле, как вы можете теперь видеть, не очень сложная. Ее освоение, по сути, заканчивается на том моменте, когда вы заучиваете названия и уравнения поверхностей (и, конечно, как они выглядят). В примере выше мы подробно рассматривали каждый шаг, но приведение уравнения к каноническому виду требует минимальных познаний в высшей математике и не должно вызывать никаких затруднений у студента.

Анализ будущего графика по имеющемуся равенству уже более сложная задача. Но для ее удачного решения достаточно понимать, как строятся соответствующие кривые второго порядка – эллипсы, параболы и прочие.

Случаи вырождения – еще более простой раздел. Из-за отсутствия некоторых переменных упрощаются не только вычисления, как уже было сказано ранее, но и само построение.

Как только вы сможете уверенно назвать все виды поверхностей, варьировать постоянные, превращая график в ту или иную фигуру – тема будет освоена.

Поверхности второго порядка

Поверхности вращения.

Поверхность $S$ называется поверхностью вращения с осью $d$, если она составлена из окружностей, которые имеют центры на прямой $d$ и лежат в плоскостях, перпендикулярных данной прямой.

Рассмотрим линию $L$, которая лежит в плоскости $P$, проходящей через ось вращения $d$ (рис. 43), и будем вращать ее вокруг этой оси. Каждая точка линии опишет окружность, а вся линия — поверхность вращения.

Рис. 10.1. Поверхность вращения.

Выберем начало декартовой прямоугольной системы координат $O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>$ на оси $d$, вектор $\boldsymbol_<3>$ направим вдоль $d$, а вектор $\boldsymbol_<1>$ поместим в плоскости $P$. Таким образом, $O, \boldsymbol_<1>, \boldsymbol_<3>$ — декартова система координат в плоскости $P$. Пусть линия $L$ имеет в этой системе координат уравнение $f(x, y)=0$.

Рассмотрим точку $M(x, y, z)$. Через нее проходит окружность, которая имеет центр на оси $d$ и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от $M$ до оси, то есть $\sqrt+y^<2>>$. Точка $M$ лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка Мь принадлежащая вращаемой линии $L$.

Точка $M_<1>(x_<1>, y_<1>, z_<1>)$ лежит в плоскости $P$, и потому $y_<1>=0$. Кроме того, $z_<1>=z$ и $|x|=\sqrt+y^<2>>$, так как $M_<1>$ лежит на той же окружности, что и $M$. Координаты точки $M_<1>$ удовлетворяют уравнению линии $L$: $f(x_<1>, z_<1>)=0$. Подставляя в это уравнение $x_<1>$ и $z_<1>$, мы получаем условие на координаты точки $M$, необходимое и достаточное для того, чтобы $M$ лежала на поверхности вращения $S$: равенство
$$
f\left(\pm \sqrt+y^<2>>, z\right)=0\label
$$
должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое можно записать также в виде
$$
f\left(\sqrt+y^<2>>, z\right)f\left(-\sqrt+y^<2>>, z\right)=0,\label
$$
и является уравнением поверхности вращения линии $L$ вокруг оси $d$.

Эллипсоид.

Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направив вектор $\boldsymbol_<3>$ сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим уравнения эллипса в следующих видах:
$$
\frac>>+\frac>>=1,\ \frac>>+\frac>>=1.\nonumber
$$
(Здесь через $c$ обозначена малая полуось эллипса.) В силу формулы \eqref уравнениями соответствующих поверхностей вращения будут
$$
\frac+y^<2>>>+\frac>>=1,\ \frac>>+\frac+y^<2>>>=1\ (a > c).\label
$$
Поверхности с такими уравнениями называются соответственно сжатым и вытянутым эллипсоидами вращения (рис. 10.2).

Рис. 10.2. Сжатый (а) и вытянутый (б) эллипсоиды вращения.

Каждую точку $M(x, y, z)$ на сжатом эллипсоиде вращения сдвинем к плоскости $y=0$ так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении \(\lambda Рис. 10.3. Эллипсоид.

Эллипсоид так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения \eqref видно, что начало канонической системы координат — центр симметрии эллипсоида, а координатные плоскости — его плоскости симметрии.

Эллипсоид можно получить из сферы $x^<2>+y^<2>+z^<2>=a^<2>$ сжатиями к плоскостям $y=0$ и $z=0$ в отношениях $\lambda=b/a$ и $\mu=c/a$.

В этой статье нам часто придется прибегать к сжатию, и мы не будем его каждый раз описывать столь подробно.

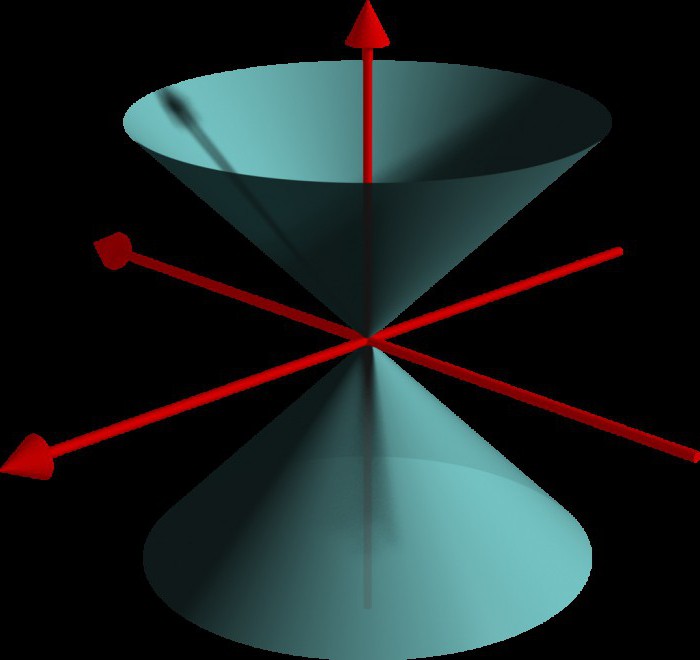
Конус второго порядка.

Рассмотрим на плоскости $P$ пару пересекающихся прямых, задаваемую в системе координат $O, \boldsymbol_<1>, \boldsymbol_<3>$ уравнением $a^<2>x^<2>-c^<2>z^<2>=0$. Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение
$$
a^<2>(x^<2>+y^<2>)-c^<2>z^<2>=0\label
$$
и носит название прямого кругового конуса (рис. 10.4). Сжатие к плоскости $y=0$ переводит прямой круговой конус в поверхность с уравнением
$$
a^<2>x^<2>+b^<2>y^<2>-c^<2>z^<2>=0\label
$$
называемую конусом второго порядка.

Обратите внимание на то, что левая часть уравнения \eqref — однородная функция, и поверхность является конусом в смысле определения, введенного ранее.

Рис. 10.4. Прямой круговой конус.

Однополостный гиперболоид.

Однополостный гиперболоид вращения — это поверхность вращения гиперболы
$$
\frac>>-\frac>>=1\nonumber
$$
вокруг той оси, которая ее не пересекает. По формуле \eqref мы получаем уравнение этой поверхности (рис. 10.5)
$$
\frac+y^<2>>>-\frac>>=1.\label
$$

Рис. 10.5. Однополостный гиперболоид вращения.

В результате сжатия однополостного гиперболоида вращения к плоскости $y=0$ мы получаем однополостный гиперболоид с уравнением
$$
\frac>>+\frac>>-\frac>>=1.\label
$$

Интересное свойство однополостного гиперболоида — наличие у него прямолинейных образующих. Так называются прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие, уравнения которых можно получить следующим образом.

Покажем на примере, как найти образующие, проходящие через данную точку поверхности. Рассмотрим поверхность $x^<2>+y^<2>-z^<2>=0$ и точку $M_<0>(1, 1, 1)$ на ней. Подставляя координаты $M_<0>$ в уравнения \eqref, мы получаем условия на $\lambda$ и $\mu$: $2\lambda=2\mu$ и $0 \cdot \lambda=0 \cdot \mu$. Первое из них определяет $\lambda$ и $\mu$ с точностью до общего множителя, но только с такой точностью они и нужны. Подставляя эти значения в \eqref, получаем уравнения прямолинейной образующей
$$
x+z=1+y,\ x-z=1-y.\nonumber
$$

Она проходит через $M_<0>$, так как $\lambda$ и $\mu$ так и выбирались, чтобы координаты $M_<0>$ удовлетворяли этой системе. Аналогично, подставляя координаты $M_<0>$ в (10), находим условия на $\lambda’$ и $\mu’$: $2\mu’=0$ и $2\mu’=0$. Коэффициент $\lambda’$ можно взять любым ненулевым, и мы приходим к уравнению второй образующей: $x=z$, $y=1$.

Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.

Двуполостный гиперболоид.

Двуполостный гиперболоид вращения — это поверхность, получаемая вращением гиперболы
$$
\frac>>-\frac>>=1\nonumber
$$
вокруг той оси, которая ее пересекает. По формуле \eqref мы получаем уравнение двуполостного гиперболоида вращения
$$
\frac>>-\frac+y^<2>>>=1.\label
$$
В результате сжатия этой поверхности к плоскости у=0 получается поверхность с уравнением
$$
\frac>>-\frac>>-\frac>>=1.\label
$$

Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида \eqref, называется двуполостным гиперболоидом (рис. 10.6). Двум ветвям гиперболы здесь соответствуют две не связанные между собой части (“полости”) поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывала всю поверхность.

Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.

Рис. 10.6. Двуполостный гиперболоид вращения.

Эллиптический параболоид.

Вращая параболу $x^<2>=2pz$ вокруг ее оси симметрии, мы получаем поверхность с уравнением
$$
x^<2>+y^<2>=2pz.\label
$$
Она называется параболоидом вращения. Сжатие к плоскости $y=0$ переводит параболоид вращения в поверхность, уравнение которой приводится к виду
$$
\frac>>+\frac>>=2z.\label
$$

Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом (рис. 10.7).

Рис. 10.7. Эллиптический параболоид.

Гиперболический параболоид.

По аналогии с уравнением \eqref мы можем написать уравнение
$$
\frac>>-\frac>>=2z.\label
$$

Поверхность, которая имеет уравнение вида \eqref в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом.

Исследуем форму этой поверхности. Для этого рассмотрим ее сечение плоскостью $x=\alpha$ при произвольном $\alpha$. В этой плоскости выберем декартову прямоугольную систему координат $O’, \boldsymbol_<2>, \boldsymbol_<3>$ с началом в точке $O'(\alpha, 0, 0)$. Относительно этой системы координат линия пересечения имеет уравнение
$$
-\frac>>=2\left(z-\frac<\alpha^<2>><2a^<2>>\right).\label
$$
Эта линия — парабола, в чем легко убедиться, перенеся начало координат в точку $O″$ с координатами $(0, \alpha^<2>/(2a^<2>))$. (Координаты этой точки относительно исходной системы координат $O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>$ в пространстве равны $(\alpha, 0, \alpha^<2>/(2a^<2>))$.)

Точка $O″$, очевидно, является вершиной параболы, ось параболы параллельна вектору $\boldsymbol_<3>$, а знак минус в левой части равенства \eqref означает, что ветви параболы направлены в сторону, противоположную направлению $\boldsymbol_<3>$. Заметим, что после переноса начала координат в точку $O″$ величина а не входит в уравнение параболы, и, следовательно, сечения гиперболического параболоида плоскостями $x=\alpha$ при всех $\alpha$ представляют собой равные параболы.

Будем теперь менять величину $\alpha$ и проследим за перемещением вершины параболы $O″$ в зависимости от $\alpha$. Из приведенных выше координат точки $O″$ следует, что эта точка перемещается по линии с уравнениями
$$
z=\frac><2a^<2>>,\ y=0\nonumber
$$
в системе координат $O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>$. Эта линия — парабола в плоскости $y=0$. Вершина параболы находится в начале координат, ось симметрии совпадает с осью аппликат, а ветви параболы направлены в ту же сторону, что и вектор $\boldsymbol_<3>$.

Теперь мы можем построить гиперболический параболоид следующим образом: зададим две параболы и будем перемещать одну из них так, чтобы ее вершина скользила по другой, оси парабол были параллельны, параболы лежали во взаимно перпендикулярных плоскостях и ветви их были направлены в противоположные стороны.

При таком перемещении подвижная парабола описывает гиперболический параболоид (рис. 10.8).

Рис. 10.8. Гиперболический параболоид. $OB$ — неподвижная парабола, $KLM,\ NOP,\ QRS$ — положения подвижной параболы.

Сечения гиперболического параболоида плоскостями с уравнениями $z=\alpha$ при всевозможных $\alpha$ — гиперболы. Эти сечения нарисованы на рис. 10.9.

Рис. 10.9. Сечения гиперболического параболоида

Выводятся эти уравнения так же, как и уравнения прямолинейных образующих однополостного гиперболоида.

Рис. 10.10. Прямолинейные образующие гиперболического параболоида

Поверхности второго порядка: их виды, уравнения, примеры

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

, ,

получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, ,

получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

, .

Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду: