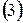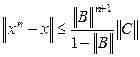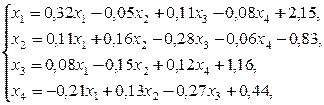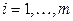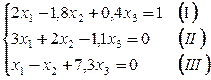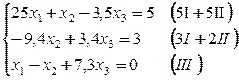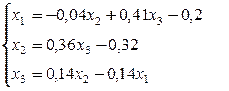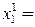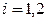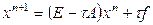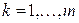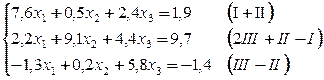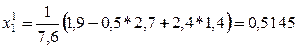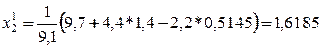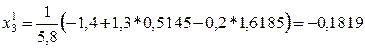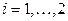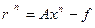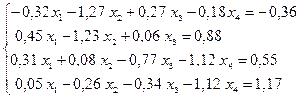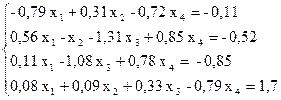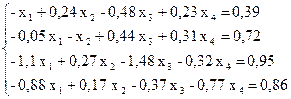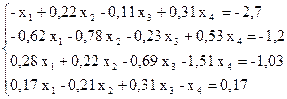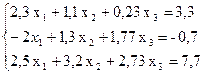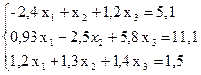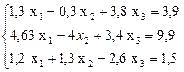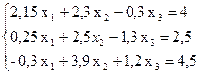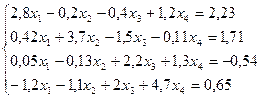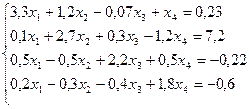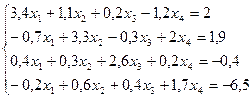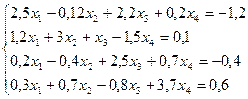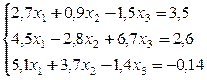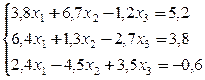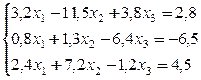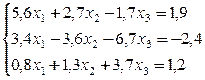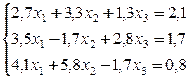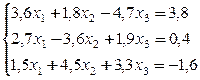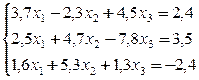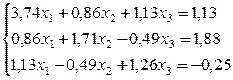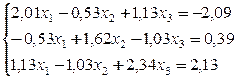Решение СЛАУ методом простой итерации
Назначение сервиса . Онлайн-калькулятор предназначен для решения СЛАУ методом простой итерации в онлайн режиме (см. пример решения). Для проверки решения генерируется шаблон в Excel .
- Шаг №1
- Шаг №2
- Видеоинструкция
Рассмотрим достаточные условия сходимости итерационной последовательности
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:

Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ1: 
б) в пространстве с метрикой ρ2: 
в) в пространстве с метрикой ρ3: 
Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:
Последовательные приближения будем искать по формулам:
Получаем:
x 1 =(-1.9022; 0.4889; 2.1456), x 2 =(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ1 вычисляем коэффициент μ 
Вычисляем погрешность:
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.
Метод итераций для системы уравнений в Excel
Для вычисления точности epsilon .
Итерация №1: =ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2: =ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.
Итерационные методы решения системы линейных алгебраических уравнений
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = — a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε
В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) — x ( n ) ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 — 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) — x ( n ) ε
Далее вычисляем нормы разности векторов:
x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x — τ ( A x — b ) , τ — итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .
Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .
Итерационные методы решения систем линейных уравнений
Меню специального перетаскивания. Наведите указатель мыши на значок Мой компьютер, нажмите правую кнопку мыши и, не отпуская ее, переместите мышь. Отпустите кнопку – откроется так называемое меню специального перетаскивания. Для большинства объектов это меню содержит пункты: Копировать, Переместить, Создать ярлык и Отменить. Для особых объектов, таких как Мой компьютер, Корзина и др., меню содержит пункты: Создать ярлык и Отменить. Выберите пункт Отменить и нажмите левую кнопку мыши.
1. Каким образом можно получить всплывающую подсказку?
Задержав курсор на объекте
2. Как развернуть окно MS-DOS на весь экран?
3. Как правильно произвести двойной щелчок?
Быстро нажать 2 раза левой кнопкой мыши на объект
4. Как открыть контекстное меню?
Нажать правую кнопку мыши
5. Как перетащить значок, окно программы в другое место?
Нажать на значок левой кнопкой мыши и не отпуская перетащить в нужное место
6. Каким образом можно выделить группу объектов?
Левым кликом мыши объединить нужные объекты
7. Как производится специальное перетаскивание?
Правым кликом мыши перетащить объект
8. Каковы преимущества специального перетаскивания?
Доступно контекстное меню со специальными функциями
Итерационные методы решения систем линейных уравнений
Итерационные методы решения систем линейных уравнений отличаются самоисправляемостью и простотой реализации на ЭВМ. Итерационные методы требуют задания начальных приближений. Сходимость итерационных методов зависит от свойств матрицы системы и выбора начальных приближений.
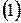
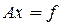
где 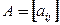
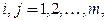
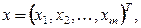
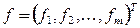
1. Метод итераций
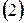
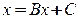
Метод итераций для системы (2) имеет вид
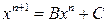
Теорема.Если 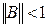
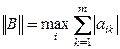
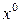
В качестве начального приближения обычно выбирается вектор свободных членов 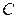
Пример. Методом итераций решить систему линейных уравнений
предварительно оценив число необходимых для этого шагов, 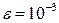
Число шагов, дающих ответ с точностью до 0,001, определим из соотношения (3). Здесь
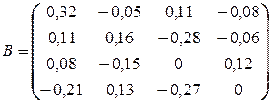
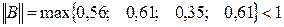
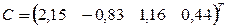
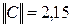
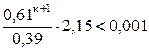
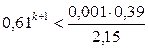
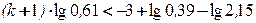
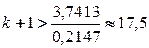
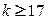
В качестве нулевого приближения выбираем вектор С.
Вычисления расположим в таблице
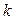 | 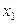 | 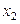 | 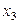 | 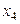 |
| 2,15 | -0,83 | 1,16 | 0,44 | |
| 2,9719 | -1,0775 | 1,5093 | -0,4326 | |
| 3,3555 | -1,0721 | 1,5075 | -0,7317 | |
| 3,5017 | -0,0106 | 1,5015 | -0,8111 | |
| 3,5511 | -0,9277 | 1,4944 | -0,8312 | |
| 3,5637 | -0,9563 | 1,4834 | -0,8298 | |
| 3,5678 | -0,9566 | 1,4890 | -0,8332 | |
| 3,5700 | -0,9575 | 1,4889 | -0,8356 | |
| 3,5709 | -0,9573 | 1,4890 | -0,8362 | |
| 3,5712 | -0,9571 | 1,4889 | -0,8364 | |
| 3,5713 | -0,9570 | 1,4890 | -0,8364 |
Метод Якоби для системы (1) в координатной форме имеет вид
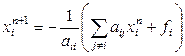
Теорема.Пусть 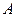
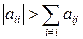
Тогда метод Якоби сходится.
Если систему (1) представить в виде (2), то можно оценить количество итераций по формуле (3).
Пример. Методом Якоби решить систему линейных уравнений
предварительно приведя матрицу системы к матрице с диагональным преобладанием и оценить число необходимых шагов для достижения точности 0,001.
Приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк:
Для оценки числа итераций запишем эту систему в виде (2), поделив каждое уравнение на диагональный элемент:
Число шагов, дающих ответ с точностью до 0,001, определяется из соотношения (3). Здесь
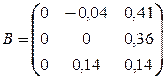
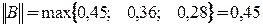
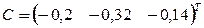
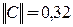
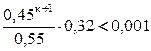
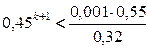
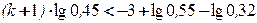
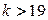
Нулевое приближение 
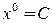
Вычислим первое приближение
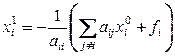
где 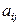
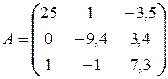
а 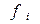
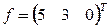
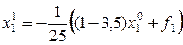
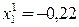
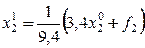
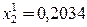
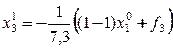
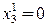
Для окончания вычислений нужно произвести 20 итераций.
3. Метод простой итерации
Метод простой итерации для системы (1) имеет вид
или в канонической форме
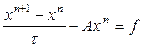
где 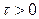
Теорема.Если 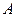
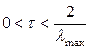
Теорема.Если 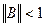
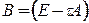
Пример.Пусть матрица A имеет вид
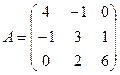
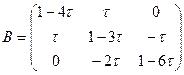
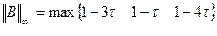
Выберем 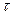
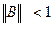
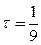
Число итераций, необходимое для заданной точности, можно вычислить как в случае метода итераций.
4. Метод Зейделя
Итерационный метод Зейделя для системы (1) в координатной форме имеет вид
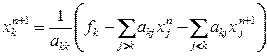
Теорема.Если 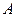
Теорема.Если 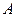
Пример. Методом Зейделя решить с точностью 0,001 систему линейных уравнений
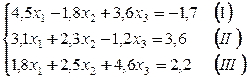
приведя ее к виду, удобному для итераций.
Приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк
Нулевое приближение 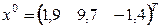
Окончание вычислений определяется условием
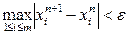
где 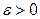
5. Метод верхней релаксации
Метод верхней релаксации является обобщением метода Зейделя. В координатной форме метод верхней релаксации имеет следующий вид
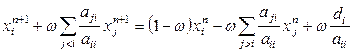
При 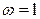
Теорема.Если 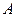
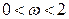
Окончание вычислений определяется условием
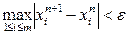
где 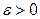
6. Метод минимальных невязок
Метод минимальных невязок определен для систем уравнений с симметричной положительно определенной матрицей 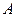
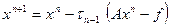
где параметр 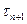
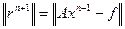
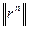
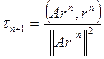
Теорема.Если 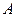
Окончание вычислений определяется условием
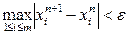
где 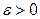
7. Метод скорейшего спуска
Если в формуле (4) итерационный параметр 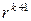
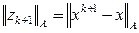
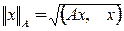
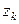
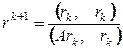
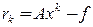
Теорема.Пусть А – симметричная положительно определенная матрица, тогда метод скорейшего спуска сходится.
Окончание вычислений определяется условием
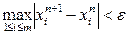
где 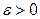
Задачи
Методом итераций решить системы линейных уравнений, предварительно приведя их к виду, удобному для итераций и оценив число необходимых для этого шагов, 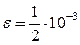
Методом Якоби решить системы линейных уравнений, предварительно приведя матрицу системы к матрице с диагональным преобладанием и оценив число необходимых шагов для достижения точности 0,001.
Методом простой итерации решить систему линейных уравнений с точностью до 0,001.
Методом Зейделя решить системы линейных уравнений, приведя их к виду, удобному для итераций, 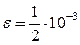
Методом верхней релаксации решить системы линейных уравнений, приведя их к виду, удобному для итераций, 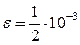
Решить системы линейных уравнений методом минимальных невязок и методом скорейшего спуска, 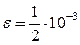
| | | следующая лекция ==> | |
| Методические указания. | | | Лабораторна робота №1. Методом итераций решить системы линейных уравнений, предварительно приведя их к виду, удобному для итераций и оценив число необходимых для этого шагов |
Дата добавления: 2015-01-09 ; просмотров: 5512 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/iteratsionnye-metody-reshenija-slau/
http://helpiks.org/2-1750.html