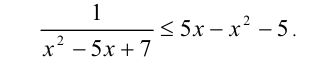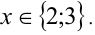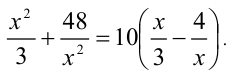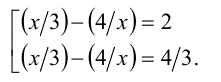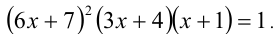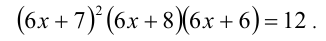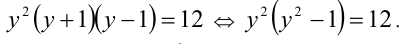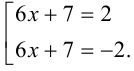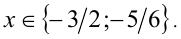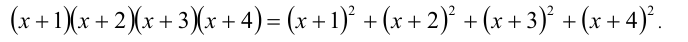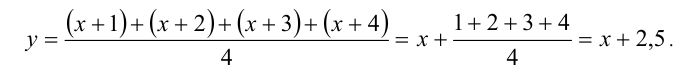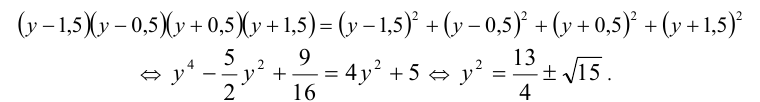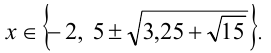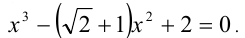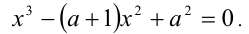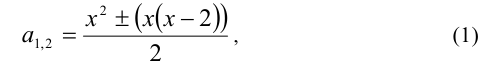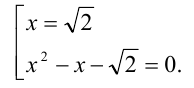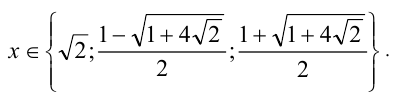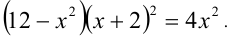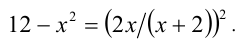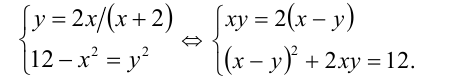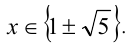Как проводить замену в уравнении

Метод замены переменной

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение \(x+\frac<1>\) буквой \(t\).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно \(t\), после чего, сделав обратную замену, вычислим \(x\).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение \(\sin x\) буквой \(t\).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Примеры использования метода замены переменной

Заметим, что \(x^4=(x^2 )^2\) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя \(x^2\) на \(t\).

Мы нашли чему равно \(t\), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: \(±1\); \(±\) \(\frac<1><2>\) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти \(x\), а не \(t\)! Поэтому возврат к \(x\) — строго обязателен!

Пример. Решить неравенство: \(\log^2_3⁡x-\log_3⁡x-2>0\)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Метод замены переменных при решении уравнений и неравенств

Метод замены переменных

Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.

Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.

Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.

Пример №350.

Решение:

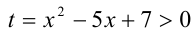
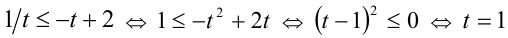
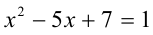
Положим . Тогда необходимо решить неравенство . Выполнив обратную подстановку, получим квадратное уравнение , решив которое, приходим к ответу. Ответ:

В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.

Пример №351.

Решить уравнение

Решение:

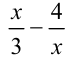
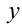
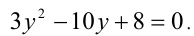
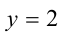
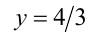
Обозначим разность через , тогда уравнение перепишется в виде Это уравнение имеет два корня и , что приводит к совокупности уравнений

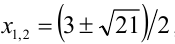
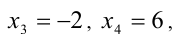
Первое уравнение даёт корни , а второе — которые и будут решениями исходного уравнения.

В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.

Пример №352.

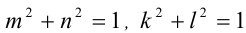
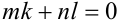
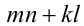
Известно, что и . Чему равно значение ?

Решение:

Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству

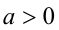
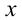
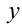
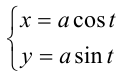
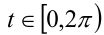
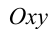
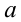
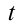
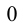
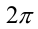
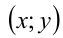
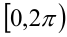
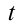
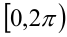
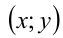
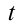
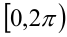
где — заданное число, то и можно представить в тригонометрическом виде , где . В самом деле, уравнение (1) задаёт на плоскости окружность радиуса с центром в начале координат. При изменении от до точка с координатами ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению из соответствует единственная пара чисел , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение из .

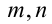
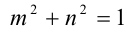
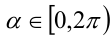
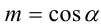
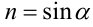
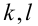
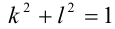
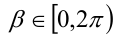
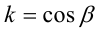
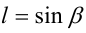
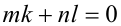
Итак, поскольку числа удовлетворяют равенству , то найдётся такое число , что , . Аналогично, поскольку числа удовлетворяют равенству , то найдётся такое число, что , . При этом условие примет вид

Выполнив тригонометрическую подстановку в искомом выражении 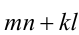, получим:

Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.

Пример №353.

Решить уравнение

Решение:

Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду

Затем сделаем подстановку 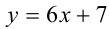, что приведёт к уравнению

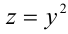
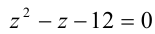
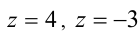
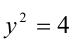
Сделав ещё одну подстановку , сведём окончательно данное биквадратное уравнение к квадратному уравнению , решив которое, находим корни . Тогда и

Ответ:

В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.

Пример №354.

Решение:

Выполним симметризирующую подстановку

Тогда уравнение примет вид

Ответ:

6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.

Пример №355.

Решение:

Введём в уравнение параметр, положив :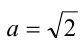

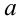
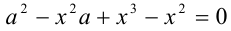
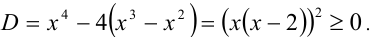
Рассмотрим теперь это уравнение как квадратное относительно . Приведём его к стандартному виду и вычислим дискриминант Найдём корни:

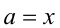
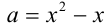
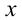
т.е. или . Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.

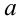
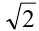
Заменяя числом , получим совокупность

Отсюда находим решения:

Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать

Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.

7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.

Пример №356.

Решение:

Так как 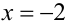не является корнем, то уравнение можно привести к равносильному виду

Положим 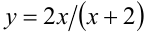, тогда уравнение сведётся к равносильной ему системе

Решая эту систему относительно 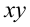и , приходим к ответу:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Методика работы с темой «замена переменной в уравнениях»

С лабый ученик — головная боль для репетитора по математике, так как традиционные методы объяснений ему не подходят. Причины этого несоответствия могут быть разными: от проблем, связанных со способностями обеспечивать достаточную скорость мышления и точную привязку мыслительных операций к определенным объектам до пропусков занятий и полного отсутствия практики общения с математическими понятиями и алгоритмами.

Особое умение репетитора выходить из таких, казалось бы, патовых ситуаций, связано с наличием в его арсенале средств различных хитрых типов объяснений текущих тем в обход каким-то навыкам и способностям, знаниям и умениям, приобретенным в результате долгого и упорного труда.

Слабые дети тоже бывают разными, но до определенной их части все-таки можно достучаться, сопоставляя изучаемые математические структуры и модели с реальными аналогами, или с явлениями похожими на них. Тогда и интерес появляется и дольше информация в памяти храниться (благо ассоциативная память включается) и быстрее приходит понимание (благо есть фундамент, на который можно хоть как-то опереться)

Замена переменной в уравнениях — одна из тем, часто попадающая в категорию до конца не понятой слабым учеником. В лучшем случае он просто заучивает алгоритм и при малейшем изменении условий его применения может растеряться. Как репетитор по математике может донести суть приема?

Рассмотрим для примера уравнение:

Сразу скажу, что методически будет правильнее сначала перенести все слагаемые в левую часть, чтобы оставшийся нуль в правой был бы постоянным, видимым и желаемым результатом вычислений при проверке корней.
Самому репетитору по математике (как и сильному ученику) решить уравнение не представляет труда. Делаем замену

Решаем уравнение

Его корни t1=-4 и t2=-1. Возвращаемся к переменной Х и решаем еще два уравнения

В первом из них нет решений, а во втором имеем единственный корень х=1.
Все ходы просты и понятны кому угодно, но только не слабому ученику, так как без соответствующих комментариев и аналогий уже на этапе перехода к уравнению

он, скорее всего, упустит нити рассуждений и потеряет взаимосвязи между числами.
На помощь репетитору по математике приходят как математические пояснения, так и примеры, не связанные напрямую с математикой. И в том и в другом случае до их использования репетитор должен развернуть структуру объекта перед ребенком и показать, как проверяется наугад взятое число на предмет попадания его в ответ. Это делается подстановкой тестируемого числа в левую часть уравнения и поэтапным подсчетом значения выражения

Сначала выполняются действия

(их результат обозначен буквой t) Затем, то, что получилось, подставляют в выражение

для сравнения его результата с нулем. Репетитору по математике желательно заострить внимание ученика на возможности такого «расчленения», а для запоминания порядка подсчета дать несколько простых упражнений. Можно попросить проверить несколько «наугад выбранных чисел», среди которых обязательно должен быть корень уравнения. Я предлагаю составить такую таблицу:

Соответствующие указатели и цветовые выделения помогут репетитору минимальным словесным описанием донести до ученика главное. Видно, что нулевой результат получился на последнем этапе вычислений при вставке числа −1 в выражение из третьей колонки. Понятно откуда эта «минус единица» пришла и какими действиями она получается.

Ставим перед учеником следующую цель: догадаться как число −1 можно было бы обнаружить, если бы мы его не знали и не видели его во втором и третьем столбике. Есть шанс, что ученик не растеряется и скажут репетитору: «надо решить уравнение t^2+5t+4 = 0». Отлично, можно идти дальше и обратить его внимание появлении числа −1 получается при подстановке х=1 в выражение

Значит х=1 — корень уравнения

Тот же ученик скажет репетитору:«надо решить уравнение x^2-2x=0»
Если понимание пришло, репетитору по математике необходимо акцентировать внимание ребенка на главной особенности уравнения, из-за которой такое решение возможно: наличие внутри левой части повторяющегося набора действий (повторяющегося выражения).

Далее. Озвучивание репетитором общего плана и техники решения всех таких уравнений со всеми сопутствующими ей атрибутами (на разобранном примере).

1) Ищем повторяющиеся выражения.
2) Обозначаем их новой буквой t.
3) Записываем шаблон будущего уравнения для нахождения иксов:

Желательно не использовать буквенные обозначения, закрепленные за другими объектами: страшим коэффициентом квадратного уравнения (буква «а»), осью ординат (буква «y») .
4) Вставляем букву t в первоначальное уравнение вместо выражения

5)Решая уравнение
Находим корни (t1 и t2), гарантирующие получение нуля в последнем столбике таблицы.
6) Подставим найденные числа в выделенный «шаблон» и решим еще два уравнения:

Таким образом найдем иксы, при подстановке которых в выражение из второй колонки таблицы эти получатся «гаранты» t1 и t2.

Фактически репетитор по математике двигается с учеником по указанной таблице справа налево.

Если ученик не самый слабый, то достаточно показать схемку:

Если репетитор чувствует, что с открытой структурой объекта, понимание все равно не приходит и ученик не может осознать (или успевает забывать) что именно показывают числа t1=-4 и t2=-1, то можно предложить сравнить подбор чисел с работой кодового замка на двери, ведущей на какой-нибудь секретный объект. Как будто кодовый замок — это буквенное выражение в левой части уравнения, а нам надо найти верный код (число для вставки вместо Х), чтобы получить нуль в результате всех действий

Тогда дверь откроется.

Это замок двойной, он состоит из двух частей :
1)«Cистема преобразований» (или коротко: «переводилка») числового кода (Х) в числовой пароль t (его «вычисляет» выражение

2)«Система проверки» пароля, которая при получении нуля в результате действий

открывает дверь.

Решить уравнение — значит найти все коды, открывающие дверь. Как это сделать?

Логично сначала узнать все пароли (t1=-4 и t2=-1), при которых дверь открывается. Для этого решим уравнение

Затем для каждого из найденных паролей и попробовать подобрать коды, которые в них будут преобразованы действиями

Эти коды — наш ответ!
При такой методике объяснений репетитору по математике будет легче удержать внимание на структуре алгоритма. Так как слова код и пароль более коротки, понятны и знакомы чем сложные для осмысления строгие математические фразы «значение переменной, при которой значение выражения . »

Если репетитору по математике опять не удалось добиться понимания, то можно привести более простую аналогию с реальностью (правда менее точную). На секретный объект имеют доступ несколько человек . Требуется пронести на него некоторые предметы. Представим себе, что эти предметы — числа (иксы). Какие из них как можно пронести?

На вопрос «как пронести» репетитору по математике ждать ответа не придется. Любой ученик скажет: «надо найти этих людей-агентов и передать с ними. Правильно! Числа −4 и −1 у нас играют роль агентов (буква t — дверь в которую они входят для получения разрешения пройти на территорию. Выражение x^2-2x похоже на карман, в который должен влезть нужный для проноса предмет (в его роли выступает число 1 из ответа).Невозможность найти корень уравнения

можно сравнить с ситуацией, когда ни один имеющийся у нас предмет не влезает в карман первого агента, а результат решения уравнения

сравнить с возможностью «запихнуть» второму посыльному в карман только одну единственную вещь : x=1 (карман очень маленький).

Можно назвать такой метод — методом аналогий. Его применение позволяет репетитору по математике в дальнейшем использовать красивые опорные слова в качестве подсказок ученику. Забыл с чего начать? Определяй агентов : t1 и t2. Если они уже найдены — определяй что залезет к ним в карман.

Осталось пожелать ученикам и репетиторам успехов в изучении темы.

Колпаков Александр Николаевич, репетитор по математике.