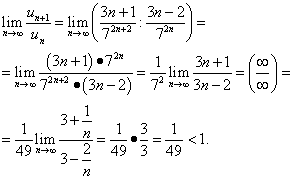Как решать дифференциальное уравнение даламбера

Лекция 6. Метод Даламбера

В этой лекции решение задачи Коши для волнового уравнения

Шаг 1. Заменим переменные (x, t) новыми переменными (ξ,η), в которых волновое уравнение примет другой вид: Такая замена выполняется по формулам

После подстановки этих производных в волновое уравнение, получим:

что и требовалось доказать.

Шаг 2. Преобразованное уравнение легко решается двумя последовательными интегрированиями (сначала по переменной η , а затем по ξ):

где C₁(η) – произвольная функция от η. Так как C(ξ) – произвольная функция, то и – также произвольная функция.

Окончательно, общее решение U(ξ,η) имеет вид

Шаг 3. Для нахождения общего решения первоначального уравнения подставим в (25) вместо ξ и η выражения (24):

Шаг 4. Определим функции C₁ и C₂, используя начальные условия из (23). После подстановки первого условия получим

Найдем производную функции U в (26) по переменной t и подставим второе условие:

В результате будем иметь систему уравнений

Если проинтегрировать второе уравнение системы (27) по x в пределах от x_o до х , то получим следующую систему:

При сложении этих уравнений получим

Если из первого уравнения системы вычесть второе уравнение, то будем иметь

Подставим теперь полученные функции в общее решение (26):

Поменяем местами пределы интегрирования во втором интеграле, стоящем в скобках в (28). В результате получим решение исходной задачи Коши

Формула (29) называется формулой Даламбера.

Далее мы исследуем решение, определяемое по формуле Даламбера.

Пространственно-временная интерпретация формулы Даламбера

При исследовании формулы Даламбера будем исходить из физического смысла волнового уравнения. Рассмотрим уравнение свободных колебаний бесконечной струны

и начальные условия

Такая задача Коши с помощью замены независимой переменной сводится к задаче (23):

Решение преобразованной задачи имеет вид (см. формулу Даламбера (29):

Если теперь в эту формулу вместо τ подставить at, то получится решение исходной задачи

Прежде, чем перейти к физической интерпретации этой формулы, сделаем следующее замечание.

Замечание. Рассмотрим в отдельности функции C₁(x-at) и C₂(x-at), входящие в общее решение (26) (коэффициент а в них появился потому, что нас сейчас интересует более общее уравнение (30)). Начнем с функции C₁(x-at) и построим графики этой функции при возрастающих значениях t: t=t_o, t=t₁, t=t₂ и т.д. (см. рис. 8).

Если по очереди проецировать эти картинки на экран (как в мультфильмах), то они «побегут» вправо. Процесс передвижения отклонения по струне называется волной. При этом коэффициент а является скоростью распространения волны. В самом деле, предположим, что параллельно оси х движется наблюдатель со скоростью а. Пусть в некоторый момент t_o он находился в точке x_o. Тогда за промежуток наблюдатель сместится вправо на величину и окажется в точке Если в точке x_o наблюдатель видел отклонение струны на величину то в момент t величина отклонения – будет точно такой же! То есть наблюдатель будет видеть форму струны не изменяющейся.

Вторая функция C₂(x-at) тоже представляет собой волну, но только она будет распространяться со скоростью а влево. Часто функции C₁(x-at) и C₂(x-at) называют, соответственно, прямой и обратной волной. Таким образом, общее решение U(x,t) (формула (26)) волнового уравнения является суперпозицией прямой и обратной волны.

Теперь дадим интерпретацию формулы Даламбера для двух частных случаев.

СЛУЧАЙ 1. Предположим, что начальное отклонение отлично от нуля, а начальная скорость равна нулю. Это означает, что начальные условия имеют вид

При таких начальных условиях получается решение задачи Коши, которое называется волной отклонения. Уравнение волны отклонения определяется формулой Даламбера

то есть решение U в некоторой точке x_o в момент времени t_o зависит от значений начальной функции φ в двух точках на оси х: в точке (x_o — at_o) и в точке (x_o + at_o) (см. рис. 9).

Значение U равно среднему арифметическому значений начальной функции φ в точках (x_o — at_o) и (x_o + at_o). На рис. 9 изображена плоскость xOt, которая называется фазовой плоскостью. На оси х указаны точки (x_o — at_o, 0) и (x_o + at_o, 0), в которых начальные отклонения струны определяют величину отклонения струны в точке x_o в момент времени t_o. Эти точки являются точками пересечения прямых x — at = x_o — at_o и x + at = x_o + at_o с осью х. Указанные прямые называются характеристиками волнового уравнения. Треугольник с вершиной в точке (х_o, t_o) и основанием, которое получается при пересечении характеристик с осью х (см. рис. 9), называется характеристическим треугольником.

Используя такую интерпретацию формулы Даламбера, изобразим фазовую картину решения следующей задачи:

Замечание. На самом деле начальные отклонения струны не могут быть разрывными в точках х = -1 и х = 1, ведь струна не разрывается. Однако мы не слишком сильно погрешим против истинной картины распространения колебаний, если будем считать их кусочно постоянными. Дело в том, что, во-первых, рассматриваются очень малые колебания струны, и, во-вторых, малые изменения начальных значений незначительно влияют на решение задачи.

На рисунке 10 изображена фазовая плоскость x0t. Решение U(x,t) задачи отлично от нуля только в заштрихованных областях, причем начальное отклонение распространяется с одинаковой скоростью в двух противоположных направлениях – возникает прямая и обратная волны. Границы этих областей – это характеристики волнового уравнения: x — at = -1, x — at = 1, x + at = -1, x + at = 1.

Если рассмотреть процесс колебания некоторой фиксированной точки струны x = x_o, то нетрудно заметить, что она колеблется только в конечный промежуток времени: от момента до момента , то есть В остальное время точка x_o находится в покое. Говорят, что в момент t₁ через точку x = x_o проходит передний фронт волны, а в момент t₂ — задний фронт волны. Вообще, фронтом волны называется граница между возмущенной (колеблющейся) и невозмущенной областями среды (точками струны). Для прямой волны уравнение переднего фронта x — at = 1, а заднего фронта x — at = -1. Для обратной волны, соответственно, x + at = -1 — уравнение переднего фронта, а x + at = 1 — заднего фронта.

СЛУЧАЙ 2. Пусть начальное отклонение равно нулю, а начальная скорость отлична от нуля. Это означает, что начальные условия имеют вид

В этом случае решение задачи Коши называют волной импульса. Оно имеет вид (см. формулу Даламбера)

то есть решение U в некоторой точке x_o в момент времени t_o зависит от начальных скоростей ψ во всех точках отрезка [x_o — at_o , x_o + at_o] (см. рис 11). Значение U равно (интегральному) среднему значению начальной скорости на отрезке [x_o — at_o , x_o + at_o], умноженному на промежуток времени t.

На рис. 11 изображена фазовая плоскость x0t. Точки (x_o — at_o, 0) и (x_o + at_o, 0) являются точками пересечения характеристик x — at = x_o — at_o и x + at = x_o + at_o с осью х. В качестве примера приведем фазовую картину решения следующей задачи:

Рис. 12 описывает процесс колебания струны, которой сообщается начальная единичная скорость на отрезке -1

При вычислении интеграла всегда удобно представить себе характеристический треугольник с вершиной в точке, лежащей в соответствующей области (см. рис 12). Тогда значение U(x,t) будет определяться значениями начальной функции ψ(x) в основании характеристического треугольника.

2. В области 2 функция

3. В области 3 функция

4. В области 4 функция

5. В области 6 функция

Это решение в различные моменты времени можно изобразить на плоскости x0U (см. рис 13). Здесь для простоты положим a=1.

Графики функции U(x,t), изображенные на рис. 13, задают форму струны в различные моменты времени.

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0\]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Признак Даламбера сходимости рядов: теория, примеры

Теоретические основы

Признак признак Даламбера, как и признак сравнения, радикальный признак Коши и интегральный признак Коши, является достаточным признаком сходимости рядов, так как исследование ряда с помощью этого признака даёт однозначный ответ на вопрос о том, сходится ряд или расходится. Признак Даламбера предполагает найти предел отношения некоторого ряда к предыдущему члену того же ряда. Признак Даламбера, скорее всего, работает, если в выражение ряда входят:

число в степени,
факториал,
цепочки множителей один-три-пять-семь и так далее.

Основной фигурант признака Даламбера — дробь, в числителе которой некоторый член ряда, а в знаменателе — предыдущий член того же ряда. Вычисляется предел этого отношения. Впрочем, перейдём к научной форме изложения рассматриваемого признака.

Теорема. Пусть для ряда с положительными членами при существует предел отношения (n+1)-го члена к предыдущему ему n-му члену, то есть

а) если предел отношения меньше единицы (), то ряд сходится;
б) если предел отношения больше единицы (), то ряд расходится;
в) если предел отношения равен единице (), то вопрос о сходимости ряда остаётся нерешённым.

Решаем примеры

Пример 1. Исследовать сходимость ряда с общим членом

Решение. Найдём отношение

Так как , а , то

Пример 2. Исследовать сходимость ряда

Решение. Общий член данного ряда

а следующий за ним член

Находим их отношение:

Пример 3. Исследовать сходимость ряда с общим членом

Используя признак Даламбера, получаем

Таким образом, получилась неопределённость вида ∞/∞. Раскроем её с помощью правила Лопиталя:

Поскольку l = 1, о сходимости ряда ничего определённого сказать нельзя. Необходимо дополнительное исследование. Сравним данный ряд с гармоническим. Так как при n > 1 получается ln (n + 1) 1/(n + 1), т.е. члены данного ряда, начиная со второго, больше соответствующих членов расходящегося гармонического ряда, а поэтому данный ряд также расходится.

Пример 4. Исследовать сходимость ряда с общим членом