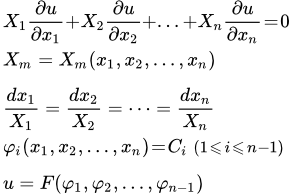Как решать дифференциальные уравнения с производной

Линейные дифференциальные уравнения в частных производных первого порядка

Линейные однородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_n – заданные функции переменных x ₁ , x ₂ , . x_n .

Чтобы решить линейное однородное уравнение в частных производных первого порядка:

необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ ₁( x ₁ , x ₂ , . x_n ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n ) = C ₂ ,
.
φ_{n- 1} ( x ₁ , x ₂ , . x_n ) = C_{n- 1} ,
где C_k – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_{n+ 1} – заданные функции от переменных x ₁ , x ₂ , . x_n и z .

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ ₁( x ₁ , x ₂ , . x_n , z ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n , z ) = C ₂ ,
.
φ_n ( x ₁ , x ₂ , . x_n , z ) = C_n .
После чего сразу получаем общий интеграл в неявном виде:

где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ ₁ = F ( φ ₂ , φ ₃ , . φ_n ) ,
φ ₂ = F ( φ ₁ , φ ₃ , . φ_n ) ,
и т. д.

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение:

Здесь переменные уже разделены, интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда

Подставим во второе уравнение:

Или:

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение C₁ = x y 2 :

Итак, мы нашли два интеграла уравнения характеристик:

Общее решение исходного уравнения в частных производных имеет вид:

где F — произвольная функция от двух аргументов F(φ₁, φ₂) . Найдем ее вид из граничного условия
при .

Рассматриваем решение на границе.
Положим x y = –1 :

Отсюда

На границе
.

Итак, мы нашли, что на границе функция F имеет вид:
F ( φ ₁ , φ ₂ ) = φ ₁ φ ₂ .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:

Общее решение:

где F — произвольная функция от двух аргументов F ( φ ₁ , φ ₂ ) .

Неоднородное уравнение

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение:

Умножаем на 2 z и интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда
x = C ₁ y

Подставим во второе уравнение:

Или:

Замечаем, что , тогда

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение и преобразуем:

Итак, мы нашли два интеграла уравнения характеристик:

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:

Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ ₁ , φ ₂) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ ₁ = F ( φ ₂) ,
где F — произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем

Итак, мы нашли, что на границе:

.
Подставим в выражение общего интеграла:
φ ₁ = F ( φ ₂)
.
Сделаем подстановку
:
.

Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ₁ и φ₂ :

.
Умножим на a 2 y 2 .

Автор: Олег Одинцов . Опубликовано: 23-09-2014

Примеры по дифференциальным уравнениям в частных производных

Немного теории

Дифференциальным уравнением с частными производными (ДУ с ЧП) называется уравнение относительно неизвестной функции нескольких переменных (ФНП) и ее частных производных. Наивысший порядок частных производных (существенно входящих в уравнение) называется порядком этого уравнения.

ДУ с ЧП называется линейным (ЛДУ с ЧП), если неизвестная функция и ее производные входят в это ДУ линейно (в первой степени).

В этом разделе вы найдете подробно решенные задачи по темам: классификация и приведение к каноническому виду ДУ с ЧП второго порядка с двумя переменными, определение типа уравнения, решение уравнений и систем ДУ в ЧП.

ДУ с ЧП находят широкое применение в прикладных науках: квантовая механика, электродинамика, термодинамика, теория теплои массопереноса и др. при математическом описании и моделировании различных физических процессов. Поэтому такие уравнения изучаются под общим названием уравнений математической физики (примеры решений 16 задач).

Приведение к каноническому виду

Задача 1. Привести к каноническому виду уравнение

Задача 2. Привести уравнение к каноническому виду.

Задача 3. Найти общее решение уравнения, приведя его к каноническому виду:

Решение ДУ в ЧП

Задача 4. Решить уравнение Пфаффа

$$ z^2 dx +zdy +(3zx +2y)dz=0. $$

Задача 5. Решить задачу Коши для уравнения в частных производных

$$ u_-2\Delta u =(x^2+y^2+z^2)t; \quad u(t=0)=xyz, u_t(t=0)=x-y. $$

Задача 6. Найти общее решение уравнения в частных производных

Задача 7. Найти общее решение уравнения в частных производных первого порядка.

$$ xy u_x +(x-2u)u_y = yu. $$

Задача 8. Найти решение задачи Коши для уравнения в частных производных

$$ y u_x -xy u_y=2xu, \quad u(x+y=2)=1/y. $$

Задача 9. Решить систему дифференциальных уравнений в частных производных

Разные задачи на исследование ДУ в ЧП

Задача 10. Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию

Задача 11. Найти области гиперболичности, эллиптичности и параболичности уравнения и исследовать их зависимость от $l$, где $l$ – числовой параметр.

Задача 12. Найти функцию, гармоническую внутри круга радиуса $R$ c центром в начале координат и такую, что

Помощь с решением ДУ в ЧП

Если вам нужна помощь с решением задач и контрольных по дифференциальным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0\]" title="Rendered by QuickLaTeX.com" />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: